黑龙江省大庆市名校2023-2024学年高二上学期数学开学考试试卷
试卷更新日期:2023-09-07 类型:开学考试
一、单选题(本题共8个小题,每题5分,共40分)
-
1. 集合 , , 则( )A、 B、 C、 D、2. 已知是数满足 , 则对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 如图,边长为2的正方形是一个水平放置的平面图形的直观图,则图形的面积是( )
 A、 B、 C、 D、5. 已知 , 则的大小关系为( )A、 B、 C、 D、6. 已知函数的部分图像如图所示,则的值为( )
A、 B、 C、 D、5. 已知 , 则的大小关系为( )A、 B、 C、 D、6. 已知函数的部分图像如图所示,则的值为( )
 A、 B、B. C、 D、7. 设为两条直线,为两个平面,下列四个命题中,正确的命题是( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , 则8. 已知定义在上的偶函数的图像是连续的, , 在区间上是增函数,则下列结论正确的是( )A、的一个周期为6 B、在区间上单调递增 C、的图像关于直线对称 D、在区间上共有100个零点
A、 B、B. C、 D、7. 设为两条直线,为两个平面,下列四个命题中,正确的命题是( )A、若 , , 则 B、若 , , , 则 C、若 , , , 则 D、若 , 则8. 已知定义在上的偶函数的图像是连续的, , 在区间上是增函数,则下列结论正确的是( )A、的一个周期为6 B、在区间上单调递增 C、的图像关于直线对称 D、在区间上共有100个零点二、多选题(本题共4个小题,每题5分,共20分)
-
9. 下列说法正确的是( )A、命题“”的否定是“” B、若正数满足 , 则 C、函数的最小正周期是 D、半径为1,圆心角为的扇形的弧长等于10. 在中,角的对边分别为 , 则下列结论正确的是( )A、若 , 则一定是钝角三角形 B、若 , 则 C、若 , 则为等腰三角形 D、若为锐角三角形,则11. 已知a , , , , 且 , 则下列说法正确的为( )A、ab的最小值为1 B、 C、 D、12. 下列说法正确的是( )A、“”是“”的既不充分也不必要条件 B、命题“”的否定是“” C、若 , 则 D、的最大值为-2
三、填空题(本题共4个小题,每题5分,共20分)
-
13. 函数的定义域为.14. 已知 , 与的夹角为 , 则 .15. , 则 .16. 我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”.现有一“阳马”(如图所示),其中底面 , , , , 则该“阳马”的外接球的表面积为 .
四、trong>、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
17. 已知内角的对边分别为 , 设(1)、求;(2)、若的面积为 , 求的值.18. 如图,在正方体中,
 (1)、求异面直线与所成的角的大小;(2)、求二面角的大小.19. 如图,四棱锥中,底面 是矩形, , 底面 , 分别为棱的中点.
(1)、求异面直线与所成的角的大小;(2)、求二面角的大小.19. 如图,四棱锥中,底面 是矩形, , 底面 , 分别为棱的中点.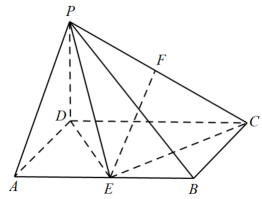 (1)、求证:平面;(2)、求证:平面平面.
(1)、求证:平面;(2)、求证:平面平面.