中考数学第一轮复习：概率

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列事件中的必然事件是（）

A、任意买一张电影票，座位号是 $2$ 的倍数 B、打开电视机，它正在播放广告 C、明年 $5$ 月 $1$ 日渭南一定会下雨 D、早上的太阳从东方升起

查看试题解析
2. 下列事件中，属于确定事件的是（）

A、抛一枚硬币，落地后正面朝上 B、菱形的两条对角线相等 C、两个非零实数的积为正 D、10只鸟关在3个笼子里，至少有一个笼子关的鸟超过3只

查看试题解析
3. 盒子里有10个球，它们只有颜色不同，其中红球有7个，黄球有2个，黑球有1个．幸幸从中任意摸一个球，下面说法正确的是（）

A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小

查看试题解析
4. 下列说法正确的是（）

A、“打开电视，播放广告”是必然事件 B、为了了解全市中学生的视力情况，选择普查 C、过十字路口，遇到绿灯是随机事件 D、若抽奖的中奖概率为 $0.5$ ，则抽奖2次就能中奖

查看试题解析
5. 将 $10$ 枚黑棋子5枚白棋子装入一个不透明的空盒子里，这些棋子除颜色外无其他差别，从盒子中随机取出一枚棋子，则取出的棋子是黑棋子的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
7. 某中学举办“传承红色精神，讲好阜新故事”演讲比赛，共设置“海州矿精神”“三沟精神”“治沙精神”三个主题，每位选手随机选取一个主题参赛．如果小明和小宇都参加比赛，他们同时选中主题“海州矿精神”的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
8. 某小组在“用频率估计概率”的实验中，统计了某种频率结果出现的频率，绘制了如图所示的折线统计图，那么符合这一结果的实验最有可能的是（）

A、掷一枚质地均匀的硬币，落地时结果是“正面向上” B、掷一个质地均匀的正六面体骰子，落地时朝上的面点数是6 C、在“石头剪刀、和”的游戏中，小明随机出的是“剪刀” D、袋子中有1个红球和2个黄球，只有颜色上的区别，从中随机取出一个球是黄球

查看试题解析
9. 吴老师在演示概率试验时，连续随机抛掷一枚质地均匀的骰子，前3次的结果是“6”，则第4次的结果是“6”的概率是（）

A、0 B、 $\frac{1}{6}$ C、 $\frac{1}{2}$ D、1

查看试题解析
10. 甲、乙两人一起玩如图4的转盘游戏，将两个转盘各转一次，指针指向的数的和为正数，甲胜，否则乙胜，这个游戏（）

A、公平 B、对甲有利 C、对乙有利 D、公平性不可预测

查看试题解析

二、填空题

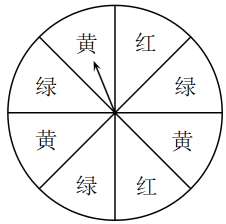
11. 布袋里装有3个红球、5个黄球、6个黑球，这些球除颜色外其余都相同，那么从这个布袋里摸出一个黑球的概率为．

查看试题解析
12. 一个质地均匀的正方形骰子的六个面上分别有 $1$ 到 $6$ 的点数，将骰子抛掷两次，抛第一次，将朝上一面的点数记为 $x$ ，抛第二次，将朝上一面的点数记为 $y$ ，则点 $(x ， y)$ 落在直线 $y = - x + 4$ 上的概率为．

查看试题解析
13. 如图，是一个材质均匀的转盘，转盘分成8个全等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止(若指针指向两个扇形的交线时，当作指向右边的扇形)，转动一次转盘，转盘停止后指针指向红色扇形的概率是．

查看试题解析
14. 如图，一块飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，每次飞镖均落在纸板上，则击中阴影区域的概率是．

查看试题解析
15. 将一副三角板中的两个三角板的两条直角边重合叠放在一起，三角板 $A O B$ 固定不动，三角板 $C O D$ 绕直角顶点O按顺时针或逆时针方向任意转动一个角 $θ (0 ° < θ < 90 °)$ ，如图所示，当这两块三角板各有一条边互相垂直时，在 $30 °$ ， $45 °$ ， $60 °$ ， $90 °$ ， $120 °$ ， $135 °$ ， $165 °$ 这七个度数中是 $∠ A O C$ 的度数的概率为.

查看试题解析
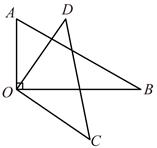16. 有四张正面分别标有数字﹣4，﹣3，﹣2，1，的不透明卡片，它们除数字不同外其他全部相同，现将它们背面朝上，洗匀后从中抽取一张，将该卡片上的数字记为a，放回后洗匀，再从中抽取一张，将该卡片上的数字记为b，则a，b使得二次函数y＝x²﹣（a+5）x+3当x≤1时y随x的增大而减小，且一元二次方程（a+2）x²+bx+1＝0有解的概率为．

查看试题解析
17. 提出问题：在不透明口袋中放入16种颜色的小球（小球除颜色外完全相同）各50个，现要确保从口袋中随机摸出的小球至少有10个是同色的，则最少需要摸出多少个小球？
建立模型：为解决上面的“问题”，我们先建立并研究下面从口袋中摸球的数学模型：

(1)、在不透明的口袋中装有红、黄、蓝三种颜色的小球各50个（除颜色外完全相同），现在要确保从口袋中随机摸出的小球至少有4个是同色的，则最少需要摸出多少个小球？为了找到解决问题的办法，我们可以把上述问题简单化：
①我们首先考虑最简单的情况：既要确保从口袋中摸出的小球至少有2个是同色的，则最少需摸出多少个小球？

假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需要再从袋中摸出1个小球就可确保至少有2个小球同色，即最少需要摸出小数的个数是：1+3=4；

②若要确保从口袋中摸出的小球至少有3个是同色的呢？

我们只需要在①的基础上，再从袋中摸出3个小球，就可以确保至少有3个小球同色，即最少需摸出小球的个数是：1+3×2=7

③若要确保从口袋中摸出的小球至少有4个小球同色，即最少需要摸出小球的个数是：1+3×3=10

④若要确保从口袋中摸出的小球至少有a个是同色的呢？即最少需要摸出小球的个数是．

(2)、模型拓展一：在不透明的口袋中装有红、黄、蓝、白、绿、紫六种颜色的小球各50个（除颜色外完全相同），现在从袋中随机摸球：
①若要确保摸出的小球至少有2个同色，则最少需摸出小球的个数是；

②若要确保摸出的小球至少有12个同色，则最少需摸出小球的个数是；

③若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是；

(3)、模型拓展二：在不透明口袋中装有n中颜色的小球各50个（除颜色外完全相同），现从袋中随机魔球：
①若要确保摸出的小球至少有3个同色，则最少需摸出小球的个数是

②若要确保摸出的小球至少有a个同色（a<50），则最少需摸出小球的个数是．

(4)、问题解决：在不透明口袋中放入16种颜色的小球（小球除颜色外完全相同）各50个，现要确保从口袋中随机摸出的小球至少有10个是同色的，则最少需摸出小球的个数是．

查看试题解析
18. 已知a、b、c、满足 $\frac{b}{a + c} = \frac{a}{c + b} = \frac{c}{a + b} = k$ ，从下列四点：① $(1 ， \frac{1}{2})$ ；②(2，1)；③ $(1 ， - \frac{1}{2})$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

查看试题解析
19. 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 $\frac{1}{2018}$ ，则密码的位数至少需要位．

查看试题解析
20. 在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( $x$ , $y$ ),其中点A,O,B不在同一直线上且-2≤ $x$ ≤2,-2≤ $y$ ≤2, $x$ , $y$ 均为整数，则所作OOAB为直角三角形的概率是.

查看试题解析

三、解答题

21. 如图是一个可以自由转动的转盘，它被分成了6个面积相等的扇形区域．数学小组的学生做转盘试验：转动转盘，当转盘停止转动时，记录下指针所指区域的颜色，不断重复这个过程，获得数据如下：

转动转盘的次数	200	300	400	1000	1600	2000
转到黄色区域的频数	72	93	130	334	532	667
转到黄色区域的频率	0.36	$m$	0.325	$n$	0.3325	0.3335

(1)、下列说法错误的是（填写序号）．

①转动转盘8次，指针都指向绿色区域，所以第9次转动时指针一定指向绿色区域；

②转动15次，指针指向绿色区域的次数不一定大于指向黄色区域的次数；

③转动60次，指针指向蓝色区域的次数一定为10.

(2)、求表中

m

，

n

的值，并估计随机转动转盘“指针指向黄色区域”的概率（精确到0.1）；

(3)、修改转盘的颜色分布情况，使指针指向每种颜色的可能性相同，写出一种方案即可．

查看试题解析

22. 有两个不透明的袋子分别装有除颜色外其余均相同的小球，甲袋中有1个红球和2个白球，乙袋中有2个红球和1个白球．

(1)、如果在甲袋中摸出一个小球，那么摸到黑球是（填“确定事件”或“随机事件”）；

(2)、如果在乙袋中摸出一个小球，那么摸到红球或白球的概率是；

(3)、如果在甲、乙两个袋子中分别随机摸出一个小球，那么摸到两球颜色相同的概率是多少？（请用列表法或树形图法说明）

查看试题解析
23. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球，其中红球3个，白球5个，黑球7个．

(1)、求任意摸出一个球是红球的概率；

(2)、求任意摸出一个球不是红球的概率．

查看试题解析
24. 某校组织学生去敬老院表演节目，表演形式有舞蹈、情景剧和唱歌3种类型．小明、小丽2人积极报名参加，从3种类型中随机挑选一种类型．求小明、小丽选择不同类型的概率．

查看试题解析

25. 对某批KN95口罩的质量进行随机抽查，结果如下表所示：

随机抽取的口罩数 $n$	100	200	400	600	800	1200
合格数 $m$	98	197	391	588	785	1176
合格的频率 $\frac{m}{n}$	▲	▲	▲	▲	▲	0.980

(1)、完成上表；（保留三位小数）

(2)、根据上表，在这批口罩中任取一个，它是合格的概率大约是．（精确到0.01）

查看试题解析

26. 如图，一个转盘被分成10个相同的扇形，颜色分别为红、黄、绿三种．甲、乙二人利用该转盘做游戏，规则是：自由转动转盘，若指针指向黄色区域则甲获胜，而指针指向绿色区域则乙获胜，你认为这个游戏对甲、乙公平吗？为什么？

查看试题解析

四、综合题

27. 小蒙设计一个抽奖游戏：如图 $1$ ，宝箱由 $7 \times 7$ 个方格组成，方格中随机放置着 $10$ 个奖品，每个方格最多能放一个奖品．

(1)、如果随机打开一个方格，获得奖品的概率是．

(2)、为了增加趣味性，小蒙优化了这个游戏．小雨参加游戏，第一次没有获得奖品，但是呈现了数字 $2$ ，如图 $2$ ．小蒙解释，这说明与这个方格相邻的 $8$ 个方格（即区域 $A$ ）中有两个放置了奖品，进行第二次抽奖，小雨将有两种选择，打开区域 $A$ 中的小方格，或者打开区域 $A$ 外的小方格．为了尽可能获得奖品，你建议小雨如何选择？请说明理由．

查看试题解析
28. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球，其中红球3个，白球5个，黑球若干个．若从中任意摸出一个白球的概率是 $\frac{1}{3}$ ．

(1)、求盒子中黑球的个数；

(2)、求任意摸出一个球是黑球的概率；

(3)、能否通过只改变盒子中白球的数量，使得任意摸出一个球是红球的概率为 $\frac{1}{4}$ ，若能，请写出如何调整白球数量．

查看试题解析
29. 小明和小强都想参加学校社团组织的暑假实践活动，但只有一个名额，小明提议用如下的办法决定谁去参加活动：将一个转盘9等分，分别标上1至9九个数字，随意转动一次转盘，若转到奇数，小明去参加活动；若转到偶数，小强去参加活动．

(1)、转盘转到奇数的概率是多少？

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析
30. 木盒内有四个形状、大小完全相同的小球，分别标注数字 $1$ 、 $2$ 、 $3$ 、 $4$ ．

(1)、从木盒内随机摸取一个小球，球上标注的数字是偶数的概率是；

(2)、从木盒内连续摸出两个小球组成一个两位数（摸出后不放回），将第一次摸出的数作为十位数字，将第二次摸出的数作为个位数字，请用树状图或列表法求出这个两位数是3的倍数的概率．

查看试题解析
31. 概率与统计在我们日常生活中应用非常广泛，请直接填出下列事件中所要求的结果：

(1)、有5张背面相同的纸牌，其正面分别标上数字“5”、“7”、“8”、“2”、“0”，将这5张纸牌背面朝上洗匀后摸出一张牌是奇数的概率为

(2)、七巧板是我国古代劳动人民的发明之一，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图是一个用七巧板拼成的正方形飞镖游戏板，某人向该游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是

查看试题解析
32. 垃圾分类工作是今年全国住房和城乡建设工作会议部署的重点工作之一．为营造人人参与垃圾分类的良好氛围，某市环保部门开展了“让垃圾分类成为低碳生活新时尚”宣传活动，决定从A ， B ， C三名志愿者中通过抽签的方式确定两名志愿者到社区进行垃圾分类知识宣讲，抽签规则：将三名志愿者的名字分别写在三张完全相同且不透明卡片的正面，把三张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的两张卡片中随机抽取第二张卡片，记下名字．

(1)、从三张卡片中随机抽取一张，恰好是“B志愿者”的概率是；

(2)、按照抽签规则，请你用列表法或画树状图法表示出两次抽签所有可能的结果，并求出A ， B两名志愿者同时被抽中的概率．

查看试题解析
33. 已知矩形ABCD的边AB=21，BC=19，r是给定的小于1的正实数.

(1)、在矩形ABCD内任意放入114个直径为1的圆.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这114个圆都没有交点（也不在某个圆的内部）；

(2)、在矩形ABCD内任意放入95个单位正方形（边长为1的正方形）.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这95个正方形都没有交点（也不在某个正方形的内部）.

查看试题解析

34. 某批乒乓球的质量检验结果如下：

抽取的乒乓球数n	200	400	600	800	1000	1600	2000
优等品的频数m	190	384	570	756	955	1520	1900
优等品的频率 $\frac{m}{n}$	a	0.96	0.95	0.945	b	0.95	c

(1)、填空：

a =

，

b =

，

c =

；

(2)、在下图中画出优等品频率的折线统计图：

(3)、从这批乒乓球中，任意抽取的一只乒乓球是优等品的概率的估计值是多少？

查看试题解析

35. 某校计划举行校园歌手大赛．九（1）班准备从A、B、C三名男生和D、E两名女生中随机选出参赛选手．

(1)、若只选1名选手参加比赛，则女生D入选的概率是；

(2)、若选2名选手参加比赛，求恰有1名男生和1名女生的概率（用画树状图或列表法求解）．

查看试题解析
36. 小亮和小芳都想参加学校社团组织的暑假实践活动，但只有一个名额，小亮提议用如下方式决定谁去参加活动：将一个转盘九等分，分别标上1至9九个数字．

(1)、任意转动一次转盘，转到的数字是2的倍数的概率是多少？

(2)、若转到的数字是2的倍数（6除外），小亮参加活动；若转到的数字是3的倍数（6除外），小芳去参加活动，若转到的数字是6或其它数字，则重新转动转盘。你认为这个游戏公平吗？请说明理由．

查看试题解析