中考数学第一轮复习:投影与视图
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
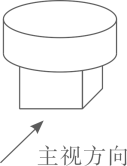
1. 当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为( )A、汽车的速度很快 B、盲区增大 C、汽车的速度很慢 D、盲区减小2. 电影院座位号呈阶梯状或下坡状的原因是( )A、减小盲区 B、增大盲区 C、盲区不变 D、为了美观3. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
 A、
A、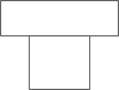 B、
B、 C、
C、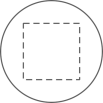 D、
D、 4. 如图,该几何体的主视图是( )
4. 如图,该几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
5. 截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )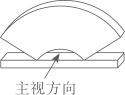 A、
A、 B、
B、 C、
C、 D、
D、 6. 由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
6. 由8个相同的立方体搭成的几何体如图所示,则它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图是由5个相同的正方体搭成的立体图形,其主视图是( ).
7. 如图是由5个相同的正方体搭成的立体图形,其主视图是( ).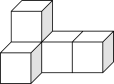 A、
A、 B、
B、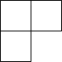 C、
C、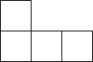 D、
D、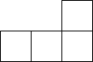 8. 如图的几何体由3个同样大小的正方体搭成,它的俯视图是( )
8. 如图的几何体由3个同样大小的正方体搭成,它的俯视图是( )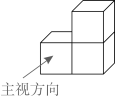 A、
A、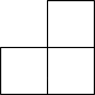 B、
B、 C、
C、 D、
D、 9. 如图所示是某几何体的三视图,则该几何体的侧面积是( )
9. 如图所示是某几何体的三视图,则该几何体的侧面积是( )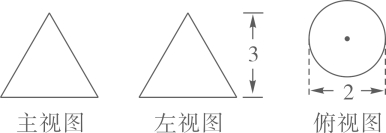 A、 B、 C、 D、10. 某几何体的三视图如图,则该几何体是( )
A、 B、 C、 D、10. 某几何体的三视图如图,则该几何体是( ) A、长方体 B、正三棱柱主视图左视图 C、球 D、圆柱11.
A、长方体 B、正三棱柱主视图左视图 C、球 D、圆柱11.由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
 A、1个 B、2个 C、3个 D、4个12. 有一圆柱形的水池,已知水池的底面直径为4米,水面离池口2米,水池内有一小青蛙,它每天晚上都会浮在水面上赏月,则它能观察到的最大视角为( )
A、1个 B、2个 C、3个 D、4个12. 有一圆柱形的水池,已知水池的底面直径为4米,水面离池口2米,水池内有一小青蛙,它每天晚上都会浮在水面上赏月,则它能观察到的最大视角为( )
A、45° B、60° C、90° D、135°13.如图是某几何体的三视图及相关数据,则判断正确的是( )
 A、a2+b2=c2 B、a2+b2=4c2 C、a2+c2=b2 D、a2+4c2=b214. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm,则投影三角板的对应边长为( )
A、a2+b2=c2 B、a2+b2=4c2 C、a2+c2=b2 D、a2+4c2=b214. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm,则投影三角板的对应边长为( )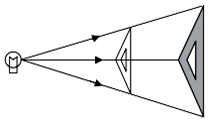 A、20cm B、10cm C、8cm D、3.2cm15. 两个人的影子在两个相反的方向,这说明( )A、他们站在阳光下 B、他们站在路灯下 C、他们站在路灯的两侧 D、他们站在月光下
A、20cm B、10cm C、8cm D、3.2cm15. 两个人的影子在两个相反的方向,这说明( )A、他们站在阳光下 B、他们站在路灯下 C、他们站在路灯的两侧 D、他们站在月光下二、填空题
-
16. 公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子AB长为23 m(直线AB过底面圆心),则小山包的高为m(π取3.14).

 17. 已知同一时刻物体的高与影子的长成正比例.身高的小明的影子长为 , 这时测得一棵树的影长为 , 则这棵树的高为.18. 某一时刻,测得身高1.6的同学在阳光下的影长为2.8 , 同时测得教学楼在阳光下的影长为25.2 , 则教学楼的高为.19. 如图,电线杆上的路灯距离地面 ,身高 的小明( )站在距离电线杆的底部(点O) 的A处,则小明的影子 长为m.
17. 已知同一时刻物体的高与影子的长成正比例.身高的小明的影子长为 , 这时测得一棵树的影长为 , 则这棵树的高为.18. 某一时刻,测得身高1.6的同学在阳光下的影长为2.8 , 同时测得教学楼在阳光下的影长为25.2 , 则教学楼的高为.19. 如图,电线杆上的路灯距离地面 ,身高 的小明( )站在距离电线杆的底部(点O) 的A处,则小明的影子 长为m.
三、作图题
-
20. 如图所示的直棱柱,其侧棱长为3cm,底面是边长为2cm的等边三角形。
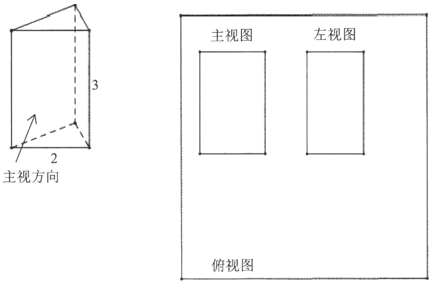 (1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。
(1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。四、解答题
-
21. 综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3s,已知小王到广告牌和公路的距离是分别是40m和80m,求该汽车的速度?
 22. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.
22. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.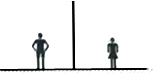
五、综合题
-
23. 汽车盲区是指驾驶员位于驾驶座位置,其视线被车体遮挡而不能直接观察到的区域.如图,△ABC、△FED分别为汽车两侧盲区的示意图,已知视线PB与地面BE的夹角∠PBE=43°,视线PE与地面BE的夹角∠PEB=20°,点A,F分别为PB,PE与车窗底部的交点,AF∥BE,AC,FD垂直地面BE,A点到B点的距离AB=1.6m.
(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)
 (1)、求盲区中DE的长度;(2)、点M在ED上,MD=1.8m,在M处有一个高度为0.3m的物体,驾驶员能观察到物体吗?请说明理由。24. 如图是可移动的3层合唱台阶,其主视图是( )
(1)、求盲区中DE的长度;(2)、点M在ED上,MD=1.8m,在M处有一个高度为0.3m的物体,驾驶员能观察到物体吗?请说明理由。24. 如图是可移动的3层合唱台阶,其主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 25. 根据信息,完成活动任务.
25. 根据信息,完成活动任务.活动一 探究某地正午太阳光下长方体高度与影子的关系.
如图1是长方体在正午阳光下投影情况,图2是图1的俯视图,通过实验测得一组数据如下表所示:

的长(cm)
的长(cm)
30
(1)、【任务1】如图2,作于点 , 设 , , 求y关于x的函数表达式.(2)、活动二 设计该地房子的数量与层数.在长方形土地上按图3所示设计n幢房子,已知每幢房子形状、高度相同,可近似看成长方体,图中阴影部分为1号楼的影子,相关数据如图所示.现要求每幢楼层数不超过 , 每层楼高度为3米.

【任务2】当1号楼层数为时,请通过计算说明正午时1号楼的影子是否落在2号楼的墙上.
(3)、【任务3】请你按下列要求设计,并完成表格.①所有房子层数总和超过.
②正午时每幢房子的影子不会落在相邻房子的墙上.
方案设计
每幢楼层数
n的值
层数总和
26. 如图所示,点P表示广场上的一盏照明灯.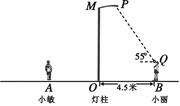 (1)、请你在图中画出小敏在照明灯照射下的影子(用线段表示);(2)、若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(1)、请你在图中画出小敏在照明灯照射下的影子(用线段表示);(2)、若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)
-