中考数学第一轮复习:锐角三角函数
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 已知一个正多边形的边心距与边长之比为 , 则这个正多边形的边数是( )A、4 B、6 C、7 D、82. 已知“为锐角时,随着的增大而增大”,则的值更靠近( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,下列等式不一定成立的( )A、a=csinA B、a=btanA C、 D、sin2A+sin2B=14. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )
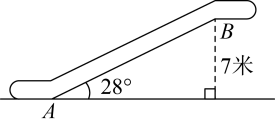 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
5. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )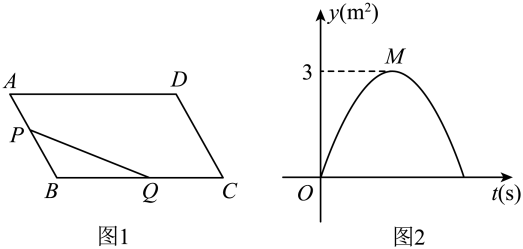 A、 B、 C、 D、6. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、 B、 C、 D、6. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )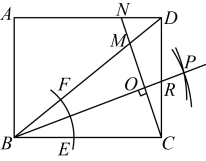 A、 B、 C、 D、47. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( )
A、 B、 C、 D、47. 如图,中, , , 于点 , 若点是线段上一动点,则的最小值为( ) A、 B、 C、 D、8. 如图,点是正方形边的中点,连接 , 将沿翻折,得到 , 延长 , 交的延长线于点 , 交于点下列结论:;;;其中正确的结论是( )
A、 B、 C、 D、8. 如图,点是正方形边的中点,连接 , 将沿翻折,得到 , 延长 , 交的延长线于点 , 交于点下列结论:;;;其中正确的结论是( ) A、 B、 C、 D、9. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
A、 B、 C、 D、9. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤10. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤10. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )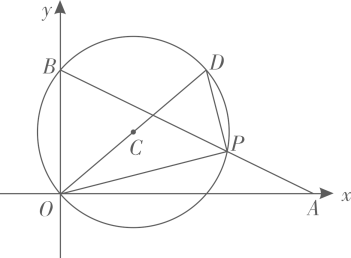 A、 B、2 C、 D、3
A、 B、2 C、 D、3二、填空题
-
11. 如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则 .
 12. 比较大小:sin35°cos45°.13. 如图,在正方形中,点E、F分别在边上, . 将沿直线CE翻折,如果点D的对应点恰好落在线段上,那么的正切值是 .
12. 比较大小:sin35°cos45°.13. 如图,在正方形中,点E、F分别在边上, . 将沿直线CE翻折,如果点D的对应点恰好落在线段上,那么的正切值是 . 14. 如图,在中, , , , 按下列步骤作图:①在和上分别截取、 , 使 . ②分别以点D和点E为圆心,以大于的长为半径作弧,两弧在内交于点M . ③作射线交于点F . 若点P是线段上的一个动点,连接 , 则的最小值是 .
14. 如图,在中, , , , 按下列步骤作图:①在和上分别截取、 , 使 . ②分别以点D和点E为圆心,以大于的长为半径作弧,两弧在内交于点M . ③作射线交于点F . 若点P是线段上的一个动点,连接 , 则的最小值是 .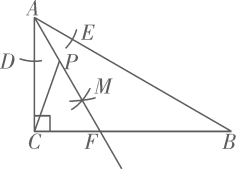 15. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 .
15. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 . 16. 将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上,两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中
16. 将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上,两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中 (1)、度.(2)、中间正六边形的中心到直线l的距离为(结果保留根号).17. 如图,在矩形中,点为矩形内一点,且 , , 则四边形的面积是 .
(1)、度.(2)、中间正六边形的中心到直线l的距离为(结果保留根号).17. 如图,在矩形中,点为矩形内一点,且 , , 则四边形的面积是 . 18. 如图,在菱形中, , , 点 , 分别是边 , 上的动点,且 , 则线段的最小值为.
18. 如图,在菱形中, , , 点 , 分别是边 , 上的动点,且 , 则线段的最小值为. 19. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 .
19. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 .
三、计算题
-
20. 先化简,再求代数式的值,其中 .
四、解答题
-
21. 如图,粮库用传送带传送粮袋,大转动轮的半径为10cm,传送带与水平面成角.假设传送带与转动轮之间无滑动,当大转动轮转时,传送带上点处的粮袋上升的高度是多少?(传送带厚度忽略不计)

 22. 如图1,是某校教学楼正厅一角处摆放的“教学楼平面示意图”展板,数学学习小组想要测量此展板的最高点到地面的高度.他们绘制了图2所示的展板侧面的截面图,并测得 , , , , 底座四边形为矩形, . 请帮助该数学学习小组求出展板最高点A到地面的距离.(结果精确到 . 参考数据: , )
22. 如图1,是某校教学楼正厅一角处摆放的“教学楼平面示意图”展板,数学学习小组想要测量此展板的最高点到地面的高度.他们绘制了图2所示的展板侧面的截面图,并测得 , , , , 底座四边形为矩形, . 请帮助该数学学习小组求出展板最高点A到地面的距离.(结果精确到 . 参考数据: , ) 23. 如图,小颖家所在居民楼高为 , 从楼顶A处测得另一座大厦顶部C的仰角是 , 而大厦底部D的俯角是 .
23. 如图,小颖家所在居民楼高为 , 从楼顶A处测得另一座大厦顶部C的仰角是 , 而大厦底部D的俯角是 . (1)、求两楼之间的距离 .(2)、求大厦的高度 .
(1)、求两楼之间的距离 .(2)、求大厦的高度 .(结果精确到 . 参考数据: , , )
24. 为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A和科技智能馆B参观学习,学生从学校出发,走到C处时,发现A位于C的北偏西方向上,B位于C的北偏西方向上,老师将学生分成甲乙两组,甲组前往A地,乙组前往B地,已知B在A的南偏西方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程(参考数据: , )
五、综合题
-
25. 如图,是的直径,点是圆上的一点,于点 , 交于点 , 连接 , 若平分 , 过点作于点 , 交于点 , 延长 , 交于点 .
 (1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.26. 公园草坪上有一架秋千 , 秋千静止时,底端到地面的距离为 , 从坚直位置开始,向右可摆动的最大夹角为 , 已知秋千的长 .
(1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.26. 公园草坪上有一架秋千 , 秋千静止时,底端到地面的距离为 , 从坚直位置开始,向右可摆动的最大夹角为 , 已知秋千的长 . (1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?27. 如图1,在长方形中, , , 动点从点出发,沿边 , 向点运动.
(1)、如图1,当向右摆动到最大夹角时,求到地面的距离;(2)、如图2,若有人在点右侧搭建了一个等腰帐篷,已知 , 帐篷的高为 , 秋千摆动的过程中是否会撞到帐篷?若不会撞到,请说明理由;若会撞到,则帐篷应该向右移动超过多少米才能不被撞到?27. 如图1,在长方形中, , , 动点从点出发,沿边 , 向点运动. (1)、当点在边上,且时,求的度数.(2)、当的面积为20时,求的长.(3)、如图2,若 , 关于直线对称.
(1)、当点在边上,且时,求的度数.(2)、当的面积为20时,求的长.(3)、如图2,若 , 关于直线对称.连结 , , 当点在边上时,求的面积.
当直线恰好经过点时,请直接写出的长度.
28. 如图,为的直径,点C在上,与相切于点A , 与延长线交于点B , 过点B作 , 交的延长线于点D . (1)、求证:;(2)、点F为上一点,连接 , , 与交于点G . 若 , , , 求的半径及的长.29. 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)、求证:;(2)、点F为上一点,连接 , , 与交于点G . 若 , , , 求的半径及的长.29. 台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域. (1)、海港C受台风影响吗?为什么?(2)、若台风的速度为25km/h,台风影响该海港持续的时间有多长?30. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶高的山峰,由山底A处先步行到达处,再由处乘坐登山缆车到达山顶处.已知点A,B.D,E,F在同一平面内,山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计)
(1)、海港C受台风影响吗?为什么?(2)、若台风的速度为25km/h,台风影响该海港持续的时间有多长?30. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶高的山峰,由山底A处先步行到达处,再由处乘坐登山缆车到达山顶处.已知点A,B.D,E,F在同一平面内,山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计) (1)、求登山缆车上升的高度;(2)、若步行速度为 , 登山缆车的速度为 , 求从山底A处到达山顶处大约需要多少分钟(结果精确到)
(1)、求登山缆车上升的高度;(2)、若步行速度为 , 登山缆车的速度为 , 求从山底A处到达山顶处大约需要多少分钟(结果精确到)(参考数据:)
31. 小亮利用所学的知识对大厦的高度进行测量,他在自家楼顶B处测得大厦底部的俯角是 , 测得大厦顶部的仰角是 , 已知他家楼顶B处距地面的高度为40米(图中点A , B , C , D均在同一平面内).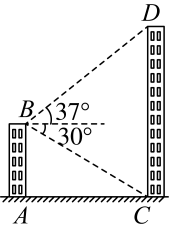 (1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).
(1)、求两楼之间的距离(结果保留根号);(2)、求大厦的高度(结果取整数).(参考数据: , , , )
32. 如图,一条笔直的公路l经过博物馆A和公园C,现要进一步开发景区B,经测量,景区B位于博物馆A的北偏东60°方向上、位于公园C的北偏东30方向上,且AC=16km (1)、求公园C与景区B的距离;(2)、为了方便游客到景区B游玩,景区管委会准备由景区B向公路l修一条距离最短的公路,不考虑其他因素,求这条最短公路的长.(结果保留根号)
(1)、求公园C与景区B的距离;(2)、为了方便游客到景区B游玩,景区管委会准备由景区B向公路l修一条距离最短的公路,不考虑其他因素,求这条最短公路的长.(结果保留根号)
-