中考数学第一轮复习:图形的相似
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 已知: , 则 的值为( )A、3 B、2 C、 D、2. 如图, 已知 , 则 CE的长为 ( )
 A、 B、 C、6 D、3. 如图,点D、E分别在△ABC的边AB、AC上,若AD:BD=2:1,点G在DE上,DG:GE=1:2,连接BG并延长交AC于点F , 则AF:EF等于( )
A、 B、 C、6 D、3. 如图,点D、E分别在△ABC的边AB、AC上,若AD:BD=2:1,点G在DE上,DG:GE=1:2,连接BG并延长交AC于点F , 则AF:EF等于( )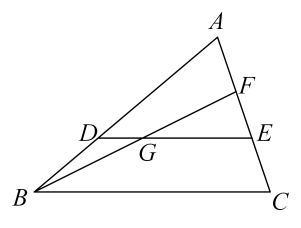 A、1:1 B、4:3 C、3:2 D、2:34. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数5. 如图,有三个矩形,其中是相似图形的是( )
A、1:1 B、4:3 C、3:2 D、2:34. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A、黄金分割数 B、平均数 C、众数 D、中位数5. 如图,有三个矩形,其中是相似图形的是( ) A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙6. 如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为 . 若矩形与原矩形相似, , 则的长为( )
A、甲和乙 B、甲和丙 C、乙和丙 D、甲、乙和丙6. 如图,四边形是一张矩形纸片.将其按如图所示的方式折叠:使边落在边上,点落在点处,折痕为;使边落在边上,点落在点处,折痕为 . 若矩形与原矩形相似, , 则的长为( ) A、 B、 C、 D、7. 如图,在△ABC中,DE∥BC,若= , 则的值为( )
A、 B、 C、 D、7. 如图,在△ABC中,DE∥BC,若= , 则的值为( ) A、 B、 C、 D、8. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( )
A、 B、 C、 D、8. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( ) A、2 B、4 C、6 D、89. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )
A、2 B、4 C、6 D、89. 如图,在中, , 点P在边上,若是的三等分线,则的长度为( )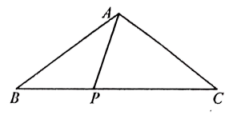 A、或5 B、或 C、或2 D、或210. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )
A、或5 B、或 C、或2 D、或210. 图1是第七届国际数学教育大会(ICME)的会徽,图2由其主体图案中相邻两个直角三角形组合而成.作菱形CDEF,使点D,E,F分别在边OC,OB,BC上,过点作于点.当时,EH的长为( )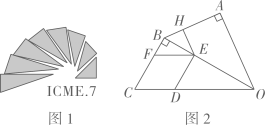 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 两个相似图形的周长比为 , 则面积比为 .12. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为 , 点对应的点记为点 , 若点恰好落在边上,则图中与一定相似的三角形是 .
 13. 如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是.
13. 如图,在平面直角坐标系中,已知A(1,0),B(2,1),D(3,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是. 14. 在平面直角坐标系中,已知点 , , , , 给出如下定义:若点P关于直线:的对称点Q在四边形的内部或边上,则称该点P为四边形关于直线的“相关点”,点是四边形关于直线:的“相关点”,且是以为腰的等腰三角形,则m的值为;直线上存在点P,使得点P是四边形关于直线:的“相关点”,则的取值范围为 .
14. 在平面直角坐标系中,已知点 , , , , 给出如下定义:若点P关于直线:的对称点Q在四边形的内部或边上,则称该点P为四边形关于直线的“相关点”,点是四边形关于直线:的“相关点”,且是以为腰的等腰三角形,则m的值为;直线上存在点P,使得点P是四边形关于直线:的“相关点”,则的取值范围为 .三、作图题
-
15. 如图,在6×6的正方形网格中,每个小正方形的边长都为1,的顶点在格点上,请使用无刻度的直尺完成以下作图(保留作图痕迹).
 (1)、在图1中,以点O为位似中心,作格点 , 使它与的位似比为2:1;(2)、在图2中,作格点(D与B不重合),使它与相似,且AC为公共边,∠A为公共角.16. 如图,在平面直角坐标系中,每个小正方格的边长都是1个单位长度,已知\的顶点坐标为 .
(1)、在图1中,以点O为位似中心,作格点 , 使它与的位似比为2:1;(2)、在图2中,作格点(D与B不重合),使它与相似,且AC为公共边,∠A为公共角.16. 如图,在平面直角坐标系中,每个小正方格的边长都是1个单位长度,已知\的顶点坐标为 .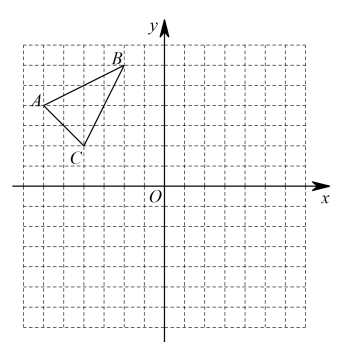
⑴画出沿着x轴向右平移5个单位长度得到的;
⑵以原点O为位似中心,将△ABC缩小为原来的 ,请在位似中心同侧画出缩小后的△A2B2C2 .⑶直接写出线段C1C2的长.
四、综合题
-
17. 如图,在中, , 为边上的点.
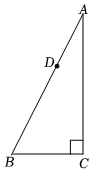 (1)、求作:平行四边形;要求:尺规作图,不写作法,保留作图痕迹(2)、在(1)所作的图形中,已知 , , , 求四边形的面积.18. 如图,在平面直角坐标系中,二次函数的图象经过点 , 与轴的交点为点和点 .
(1)、求作:平行四边形;要求:尺规作图,不写作法,保留作图痕迹(2)、在(1)所作的图形中,已知 , , , 求四边形的面积.18. 如图,在平面直角坐标系中,二次函数的图象经过点 , 与轴的交点为点和点 .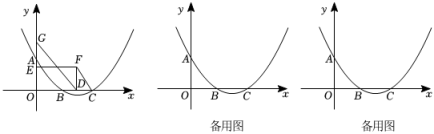 (1)、求这个二次函数的表达式;(2)、点 , 在轴正半轴上, , 点在线段上,以线段 , 为邻边作矩形 , 连接 , 设 .
(1)、求这个二次函数的表达式;(2)、点 , 在轴正半轴上, , 点在线段上,以线段 , 为邻边作矩形 , 连接 , 设 .连接 , 当与相似时,求的值;
当点与点重合时,将线段绕点按逆时针方向旋转后得到线段 , 连接 , , 将绕点按顺时针方向旋转后得到 , 点 , 的对应点分别为、 , 连接当的边与线段垂直时,请直接写出点的横坐标.
五、实践探究题
-
19. 【问题呈现】
和都是直角三角形, , 连接 , , 探究 , 的位置关系.
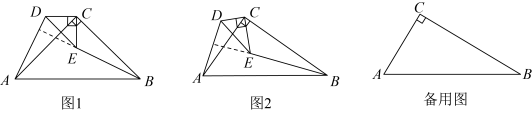 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
20. 综合与实践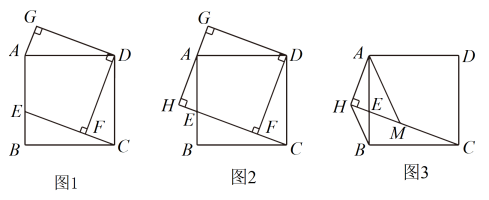 (1)、【思考尝试】
(1)、【思考尝试】数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,于点F, , , . 试猜想四边形的形状,并说明理由;
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边上一点,于点F,于点H,交于点G,可以用等式表示线段 , , 的数量关系,请你思考并解答这个问题;
(3)、【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边上一点,于点H,点M在上,且 , 连接 , , 可以用等式表示线段 , 的数量关系,请你思考并解答这个问题.