中考数学第一轮复习:轴对称变换、平移、旋转变换
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 以下图形,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中不是轴对称图形的是( )A、
2. 下列图形中不是轴对称图形的是( )A、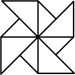 B、
B、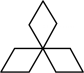 C、
C、 D、
D、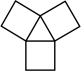 3. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )A、
3. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 已知、两点关于轴对称,则的值为( )A、5 B、1 C、 D、5. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片展开,得到的图形应是( )
4. 已知、两点关于轴对称,则的值为( )A、5 B、1 C、 D、5. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片展开,得到的图形应是( ) A、
A、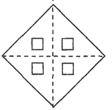 B、
B、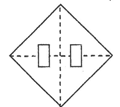 C、
C、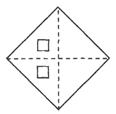 D、
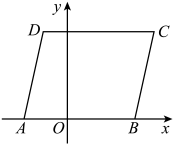
D、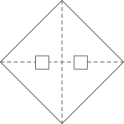 6. 如图,四盏灯笼位置A、B、C、D坐标分别是 , , , , 平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
6. 如图,四盏灯笼位置A、B、C、D坐标分别是 , , , , 平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )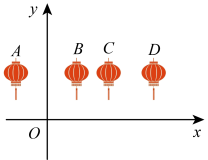 A、将D向左平移4.5个单位 B、将C向左平移5.5个单位 C、将D向左平移3.5个单位 D、将C向左平移3.5个单位7. 下面是4个能完全重合的正六边形,请仔细观察、、、四个图案,其中与所给图形不相同的是( )
A、将D向左平移4.5个单位 B、将C向左平移5.5个单位 C、将D向左平移3.5个单位 D、将C向左平移3.5个单位7. 下面是4个能完全重合的正六边形,请仔细观察、、、四个图案,其中与所给图形不相同的是( )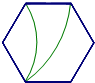 A、
A、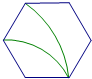 B、
B、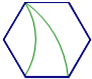 C、
C、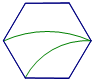 D、
D、 8. 有下列现象:①高层公寓电梯的上升:②传送带的移动;③方向盘的转动;④风车的转动;⑤钟摆的运动;⑥荡秋千运动.其中属于旋转的有( )A、2个 B、3个 C、4个 D、5个9. 如图,在平面直角坐标系中,点的坐标为 . 线段以每秒旋转90°的速度,绕点沿顺时针方向连续旋转,同时,点从点出发,以每秒移动1个单位长度的速度,在线段上,按照…的路线循环运动,则第2023秒时点的坐标为( )
8. 有下列现象:①高层公寓电梯的上升:②传送带的移动;③方向盘的转动;④风车的转动;⑤钟摆的运动;⑥荡秋千运动.其中属于旋转的有( )A、2个 B、3个 C、4个 D、5个9. 如图,在平面直角坐标系中,点的坐标为 . 线段以每秒旋转90°的速度,绕点沿顺时针方向连续旋转,同时,点从点出发,以每秒移动1个单位长度的速度,在线段上,按照…的路线循环运动,则第2023秒时点的坐标为( )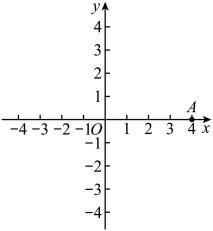 A、 B、 C、 D、10. 下列正多边形,绕其中心旋转后,能和自身重合的是 ( )A、
A、 B、 C、 D、10. 下列正多边形,绕其中心旋转后,能和自身重合的是 ( )A、 B、
B、 C、
C、 D、
D、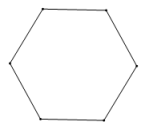 11. 已知点A关于原点对称点的坐标为(a,b),那么点A关于y轴对称点的坐标是( )A、(a,-b) B、(-a,b) C、(-a,-b) D、(a,b)12. 五星红旗上的一个五角星图案如图所示,将图案绕五角星的中心至少旋转度能与自身重合,则为( )
11. 已知点A关于原点对称点的坐标为(a,b),那么点A关于y轴对称点的坐标是( )A、(a,-b) B、(-a,b) C、(-a,-b) D、(a,b)12. 五星红旗上的一个五角星图案如图所示,将图案绕五角星的中心至少旋转度能与自身重合,则为( ) A、108 B、90 C、72 D、60
A、108 B、90 C、72 D、60二、填空题
-
13. 定义:在平面直角坐标系中,若点M关于直线的对称点在的内部(不包含边界),则称点M是关于直线的“伴随点”.如图,已知三点,连接 , 以为边作 . 若在直线上存在点N,使得点N是关于直线的“伴随点”,则n的取值范围是 .
 14. 如图,有一条直的等宽纸带按图折叠时,则图中∠a= .
14. 如图,有一条直的等宽纸带按图折叠时,则图中∠a= .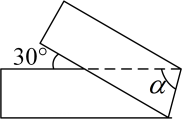 15. 室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数,如图所示,则这时的实际时间应是
15. 室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数,如图所示,则这时的实际时间应是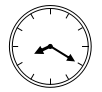 16. 如图,在中, , 将沿着BC的方向平移至 , 若平移的距离是3,则图中阴影部分的面积为 .
16. 如图,在中, , 将沿着BC的方向平移至 , 若平移的距离是3,则图中阴影部分的面积为 .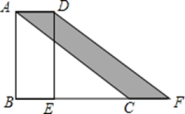 17. 如图,以点C为旋转中心,旋转后得到 , 已知 , 则 .
17. 如图,以点C为旋转中心,旋转后得到 , 已知 , 则 .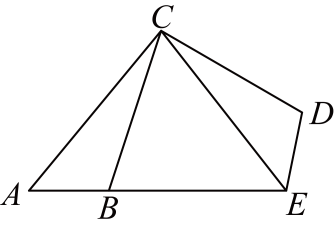 18. 如图所示,直线与x轴,y轴分别交于A,B两点,把绕点A旋转后得到 , 则点的坐标是 .
18. 如图所示,直线与x轴,y轴分别交于A,B两点,把绕点A旋转后得到 , 则点的坐标是 .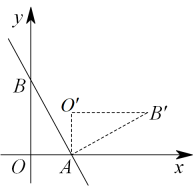 19. 如图,在中, , , . 将绕点C按顺时针方向旋转后得 , 直线、相交于点 . 取的中点 , 连接 , 则长的最大值为 .
19. 如图,在中, , , . 将绕点C按顺时针方向旋转后得 , 直线、相交于点 . 取的中点 , 连接 , 则长的最大值为 .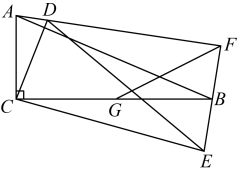 20. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,
20. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,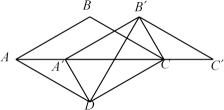 (1)、若四边形是矩形,则;(2)、的最小值为 .21. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .
(1)、若四边形是矩形,则;(2)、的最小值为 .21. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .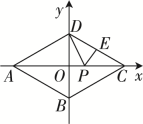 22. 如图1,有一条长方形纸带ABCD,∠DEF=15°.
22. 如图1,有一条长方形纸带ABCD,∠DEF=15°.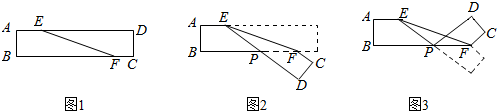 (1)、将纸带沿EF折叠,如图2所示,则∠EPB的度数为;(2)、将图2中的纸带再沿BF折叠,如图3所示,则∠CFE的度数为 .
(1)、将纸带沿EF折叠,如图2所示,则∠EPB的度数为;(2)、将图2中的纸带再沿BF折叠,如图3所示,则∠CFE的度数为 .三、计算题
-
23. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.
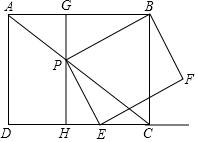 (1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.
(1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.四、作图题
-
24. 如图,和关于直线对称,和关于直线对称.
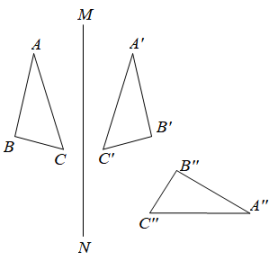 (1)、画出直线;(2)、直线与相交于点O , 试探究与直线、所夹锐角的数量关系.25. 在网格中建立如图所示的平面直角坐标系,其中、、、 .
(1)、画出直线;(2)、直线与相交于点O , 试探究与直线、所夹锐角的数量关系.25. 在网格中建立如图所示的平面直角坐标系,其中、、、 .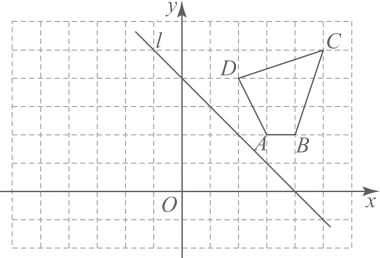 (1)、请作出四边形关于轴对称的四边形 , 并写出点的对应点的坐标;(2)、在直线上找一点 , 使得的周长最小,在图中标出的位置,并写出点的坐标(保留画图过程的痕迹).26. 如图,三角形的顶点都在方格纸的格点上,每个小方格的边长为1,将三角形向上平移4格,再向左平移3格.
(1)、请作出四边形关于轴对称的四边形 , 并写出点的对应点的坐标;(2)、在直线上找一点 , 使得的周长最小,在图中标出的位置,并写出点的坐标(保留画图过程的痕迹).26. 如图,三角形的顶点都在方格纸的格点上,每个小方格的边长为1,将三角形向上平移4格,再向左平移3格.
⑴请在图中画出平移后的三角形;
⑵画出三角形中边上的高;则三角形的面积_______;
⑶连接、 , 则线段与的关系为_______;四边形的面积_______.27. 如图,方格纸中每个小正方形的边长都是1个单位长度,建立平面直角坐标系,的三个顶点坐标分别为 , , .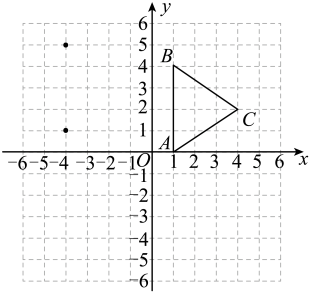 (1)、将向左平移5个单位,再向上平移1个单位,画出平移后的;(2)、画出将绕原点按顺时针方向旋转后的 , 并写出点的对应点的坐标.28. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点C的坐标为 .
(1)、将向左平移5个单位,再向上平移1个单位,画出平移后的;(2)、画出将绕原点按顺时针方向旋转后的 , 并写出点的对应点的坐标.28. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点C的坐标为 .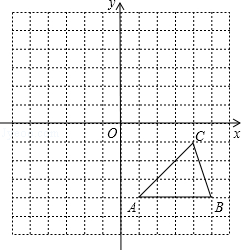
⑴把向上平移5个单位后得到对应的 , 画出;
⑵以原点O为对称中心,画出与关于原点O对称的 .
29. 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC ,
⑴△ABC与△A1B1C1关于原点O对称,写出△A1B1C1各顶点的坐标,画出△A1B1C1;
⑵以O为旋转中心将△ABC顺时针旋转90°得△A2B2C2 , 画出△A2B2C2并写出△A2B2C2各顶点的坐标.
五、实践探究题
-
30. 数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图所示的长方形纸条 , 其中 , . 然后在纸条上任意画一条线段 , 将纸片沿折叠,与交于点 , 得到 . 如图所示:
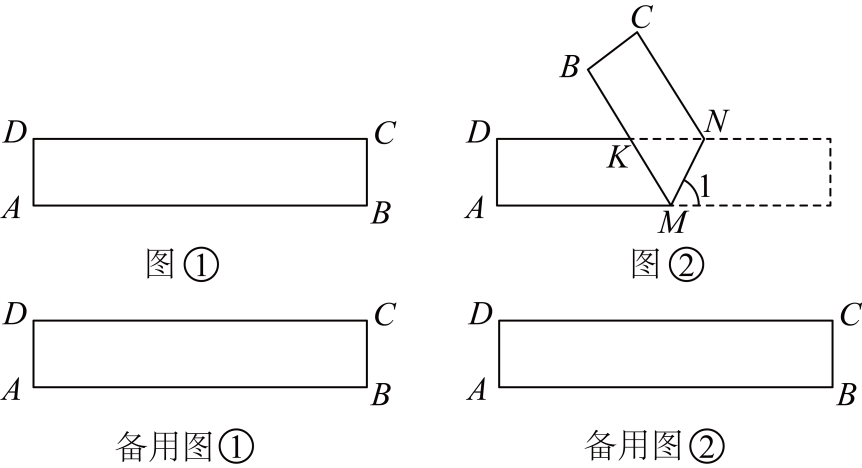 (1)、【基础回顾】在图中,若 , ∠MKN=°;(直接写出答案)(2)、【操作探究】改变折痕位置,始终是 三角形,请说明理由;(3)、爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为 , 此时的大小可以为;(4)、【拓展延伸】小明继续动手操作进行折纸,发现了面积存在最大值,请你求出这个最大值.31. 【问题情境】如图,在中, , . 点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接 , , 以为底边在其上方作等腰三角形 , 使 , 连接 .(1)、【尝试探究】
(1)、【基础回顾】在图中,若 , ∠MKN=°;(直接写出答案)(2)、【操作探究】改变折痕位置,始终是 三角形,请说明理由;(3)、爱动脑筋的小明在研究的面积时,发现边上的高始终是个不变的值.根据这一发现,他很快研究出的面积最小值为 , 此时的大小可以为;(4)、【拓展延伸】小明继续动手操作进行折纸,发现了面积存在最大值,请你求出这个最大值.31. 【问题情境】如图,在中, , . 点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接 , , 以为底边在其上方作等腰三角形 , 使 , 连接 .(1)、【尝试探究】如图1,当时,易知;
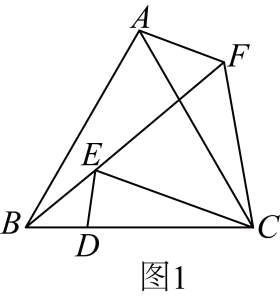
如图2,当时,则与的数量关系为;
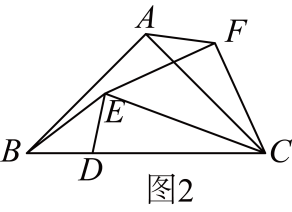 (2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由;
(2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由; (3)、【拓展应用】
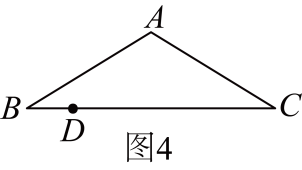
(3)、【拓展应用】如图4,当 , 且点B , E , F三点共线时.若 , , 请直接写出的长.
 32. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
32. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.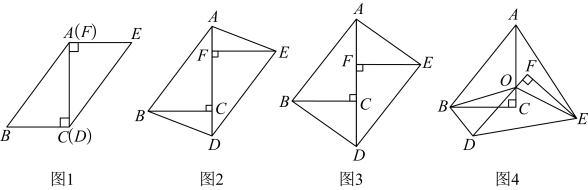
活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(1)、【思考】图2中的四边形ABDE是平行四边形吗?请说明理由.(2)、【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.(3)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.
六、综合题
-
33. 观察如图①②③中阴影部分构成的图案
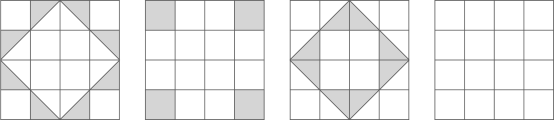
① ② ③ ④
(1)、请你写出这三个图案都具有的两个共同特征:(2)、请在图④中设计一个新的图案,使其满足(1)中的共同特征.34. 北师大版初中数学教科书七年级下册第23页告诉我们,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如由图①可以得到 , 这样就用图形面积验证了完全平方公式.请解答下列问题: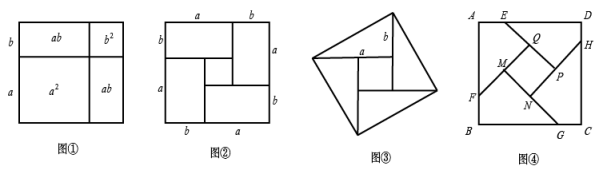 (1)、类似地,写出图②中所表示的数学等式;(2)、如图③的图案被称为“赵爽弦图”,是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲.这个图案被选为2002年在北京召开的国际数学家大会的会徽.此图由四个全等的直角三角形围成一个大正方形,中空的部分是一个小正方形,已知直角三角形的两直角边分别为 , , 若 , , 求大正方形的面积;(3)、如图④,在边长为的正方形各边上分别截取 , 当时,求正方形的面积.
(1)、类似地,写出图②中所表示的数学等式;(2)、如图③的图案被称为“赵爽弦图”,是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,它表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲.这个图案被选为2002年在北京召开的国际数学家大会的会徽.此图由四个全等的直角三角形围成一个大正方形,中空的部分是一个小正方形,已知直角三角形的两直角边分别为 , , 若 , , 求大正方形的面积;(3)、如图④,在边长为的正方形各边上分别截取 , 当时,求正方形的面积.
-