中考数学第一轮复习:命题与证明
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 下列语句中,不是命题的是( )A、两点之间线段最短 B、内错角都相等 C、连接A , B两点 D、平行于同一直线的两直线平行2. 下列说法,①同位角相等;②经过一点,有且只有一条直线与已知直线平行;③垂直于同一条直线的两条直线互相平行;④两条直线被第三条直线所截,同旁内角的平分线互相垂直;其中正确的是( )A、0个 B、1个 C、2个 D、3个3. 已知命题:如果a=b,那么|a|=|b|.该命题的逆命题是( ).A、如果a=b,那么|a|=|b| B、如果|a|=|b|,那么a=b C、如果a≠b,那么|a|≠|b| D、如果|a|≠|b|,那么a≠b4. 有8个形状大小相同的小球,其中一个略重些,其余7个重量相同.现给你一架天平,能将那个略重些的小球找到,则至少需要天平的次数是( )A、4 B、3 C、2 D、15. 用反证法证明“三角形中必有一个内角小于或等于”时,首先应假设这个三角形中( )A、有一个内角小于 B、有一个内角大于 C、每一个内角都小于 D、每一个内角都大于6. 如图,在平行四边形中,对角线和交于点 , 下列命题是真命题的是( )
 A、若 , 则平行四边形是菱形 B、若 , 则平行四边形是矩形 C、若 , 则平行四边形是矩形 D、若且 , 则平行四边形是正方形7. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:
A、若 , 则平行四边形是菱形 B、若 , 则平行四边形是矩形 C、若 , 则平行四边形是矩形 D、若且 , 则平行四边形是正方形7. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:①;②;③平分;④平分 . 其中正确的是( )
 A、①② B、①②③ C、②③④ D、①②③④8. 如题图所示,已知一个半径为2的 , P为平面内一个点,过点P作的两条切线 , , 为的一条直径,且 , 连接若干条线段的端点.若 , 下列给出的四个命题中,为假命题的是( )
A、①② B、①②③ C、②③④ D、①②③④8. 如题图所示,已知一个半径为2的 , P为平面内一个点,过点P作的两条切线 , , 为的一条直径,且 , 连接若干条线段的端点.若 , 下列给出的四个命题中,为假命题的是( )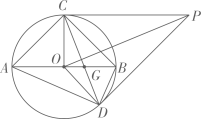 A、 B、为正三角形 C、 D、9. 如图,点C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边ΔABC和等边ΔCDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOE=120°;⑥ΔCPQ为等边三角形;⑦CO平分∠AOE;正确的有( )个.
A、 B、为正三角形 C、 D、9. 如图,点C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边ΔABC和等边ΔCDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOE=120°;⑥ΔCPQ为等边三角形;⑦CO平分∠AOE;正确的有( )个.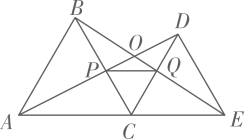 A、3个 B、5个 C、6个 D、7个10. 下列命题:① 若b=a+c时,一元二次方程一定有实数根;② 若方程有两个不相等的实数根,则方程也一定有两个不相等实数根;③ 若二次函数 , 当取、()时,函数值相等,则当x取时函数值为0;④ 若 , 则二次函数的图像与坐标轴的公共点的个数是2或3,其中正确结论的个数是( )A、1个 B、2个 C、3个 D、4个
A、3个 B、5个 C、6个 D、7个10. 下列命题:① 若b=a+c时,一元二次方程一定有实数根;② 若方程有两个不相等的实数根,则方程也一定有两个不相等实数根;③ 若二次函数 , 当取、()时,函数值相等,则当x取时函数值为0;④ 若 , 则二次函数的图像与坐标轴的公共点的个数是2或3,其中正确结论的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 把命题“垂直于同一条直线的两条直线平行”改写成“如果……,那么……”的形式是 .12. 定理“平行四边形的对角相等”的逆命题是 .13. 某校要举办秋季运动会,初一(2)班有四名同学分别想参与100m,200m,400m,和800m的比赛,其中甲同学擅长跑100m和200m,乙同学擅长跑400m和800m,丙同学擅长跑100m、200m和400m,丁同学最擅长跑100m.为了让班级取得好成绩,也让他们每个人都可以参加比赛,并且每人只能参加一项比赛,那么只能派参加400m比赛.14. 阅读下列材料:“为什么不是有理数”,完成问题.
证明:假设是有理数,
那么存在两个互质的正整数、 , 使得 , 于是 ,
∴ ▲
∵是偶数,可得是偶数.
∵只有偶数的平方才是偶数,∴也是偶数.
∴可设 , 代入,得 ▲ .可得 ▲
∴ ▲ .这样,和都是偶数,不互质,这与假设 , 互质矛盾.
这个矛盾说明,不能写成分数的形式,即不是有理数.
将下列选项依次填入材料中的画线处,正确的顺序是.(填上序号)
①; ②; ③是偶数; ④.
15. 图1是一个正方形网格,两条网格线的交点叫做格点.甲、乙两人在网格中进行游戏,规则如下:
游戏规则a.两人依次在网格中画线段,线段的起点和终点均为格点;
b.新画线段的起点为前一条线段的终点,且与任意已画出线段不能有其它公共点;
c.已画出线段的所有端点中,任意三个端点不能在同一条直线上;
d.当某人无法画出新的线段时,则另一人获胜.
如图2,甲先画出线段 , 乙随后画出线段.若这局游戏继续进行下去,最终的获胜者是.(填“甲”,“乙”或“不确定”).
 16. 金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .17. 如图,在8个格子中依次放着分别写有字母a~h的小球.
16. 金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .17. 如图,在8个格子中依次放着分别写有字母a~h的小球.
甲、乙两人轮流从中取走小球,规则如下:
①每人首次取球时,只能取走2个或3个球;后续每次可取走1个,2个或3个球;
②取走2个或3个球时,必须从相邻的格子中取走;
③最后一个将球取完的人获胜.
(1)、若甲首次取走写有b,c,d的3个球,接着乙首次也取走3个球,则(填“甲”或“乙”)一定获胜;(2)、若甲首次取走写有a,b的2个球,乙想要一定获胜,则乙首次取球的方案是 .18. “爆竹声中一岁除,春风送暖入屠苏.千门万户曈曈日,总把新桃换旧符.”春节将至,置办年货是中国寻常百姓家不可或缺的大事.小明随妈妈去置办年货,购买了灯笼、窗花、坚果,其中灯笼每只20元,窗花每张8元,坚果每包150元,若小明和妈妈一共用了428元(三种年货都有购买),则最多能买灯笼只.19. 有同样大小的三个立方体骰子,每个骰子的展开图如图1所示,现在把三个股子放在桌子上(如图2),凡是能看得到的点数之和最大是 , 最小是 . 20. 为鼓励学生居家锻炼,李老师组织线上仰卧起坐接力活动.4人为一组,每人自主设定个人目标(单位:次),组内任意2人之间均需接力一场,且每场接力2人都达到个人目标即停止,记录每场接力成绩(2人所做仰卧起坐次数之和).小贾、小易、小冰、小丁为一组,他们六场接力成绩由小到大依次为86,92,94,98,100,106.若他们设定的个人目标分别记为a,b,c,d,其中 , 且 . 根据以上信息,得到三个结论:① , ;②六场接力成绩由小到大可以依次表示为: , , , , , ;③a,b,c,d的值分别为46,40,52,54.其中正确结论的序号是 .21. 某工厂有甲、乙、丙、丁、戊五台车床.若同时启动其中两台车床,加工10000个W型零件所需时间如表:
20. 为鼓励学生居家锻炼,李老师组织线上仰卧起坐接力活动.4人为一组,每人自主设定个人目标(单位:次),组内任意2人之间均需接力一场,且每场接力2人都达到个人目标即停止,记录每场接力成绩(2人所做仰卧起坐次数之和).小贾、小易、小冰、小丁为一组,他们六场接力成绩由小到大依次为86,92,94,98,100,106.若他们设定的个人目标分别记为a,b,c,d,其中 , 且 . 根据以上信息,得到三个结论:① , ;②六场接力成绩由小到大可以依次表示为: , , , , , ;③a,b,c,d的值分别为46,40,52,54.其中正确结论的序号是 .21. 某工厂有甲、乙、丙、丁、戊五台车床.若同时启动其中两台车床,加工10000个W型零件所需时间如表:车床编号
甲、乙
乙、丙
丙、丁
丁、戊
甲、戊
所需时间(h)
13
9
10
12
8
则加工W型零件最快的一台车床的编号是 .
22. 数学真奇妙:两个有理数a和b,如果分别计算a+b,a﹣b,ab,的值,发现有三个结果恰好相同,则b= .三、解答题
-
23. 完成下面证明.
已知:如图, , , 求证: .

证明:∵(已知)
且( ),
∴(等量代换).
∴ ▲ (同位角相等,两直线平行).
∴( ).
∵(已知),
∴( ).
∴ ▲ (两直线平行,内错角相等).
∴(等量代换).
24. 已知的两条直角边及斜边长分别为 , 斜边上的高是 .求证: .
25. 如图, , , 是的角平分线.求证: . 26. 用反证法证明下列问题。
26. 用反证法证明下列问题。如图,在△ABC中,点D,E分别在AC,AB上,BD,CE相交于点O。

求证:BD和CE不可能互相平分。
四、综合题
-
27. 如图,已知点G在上,点C , D在上, , .
 (1)、求证:;(2)、若 , , 求证:;(3)、在(2)的条件下, , 求的度数.28. 已知二次函数 , 关于x的方程有下列四个命题:①是方程的根 ②是方程的根 ③该方程两根和为4 ④该方程两根同号,若其中只有1个命题为假命题,将向左平移个单位,向下平移个单位得到函数 .
(1)、求证:;(2)、若 , , 求证:;(3)、在(2)的条件下, , 求的度数.28. 已知二次函数 , 关于x的方程有下列四个命题:①是方程的根 ②是方程的根 ③该方程两根和为4 ④该方程两根同号,若其中只有1个命题为假命题,将向左平移个单位,向下平移个单位得到函数 .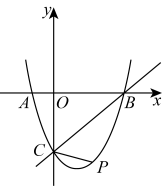 (1)、求函数与的解析式;(2)、如题图所示,已知与x轴相交于A、B两点,与y轴交于点C.点P是抛物线上位于直线BC下方一动点,当时,求点P的坐标;29. 阅读下列材料,并完成相应学习任务:
(1)、求函数与的解析式;(2)、如题图所示,已知与x轴相交于A、B两点,与y轴交于点C.点P是抛物线上位于直线BC下方一动点,当时,求点P的坐标;29. 阅读下列材料,并完成相应学习任务:勾股定理,是指直角三角形的两条直角边的平方和等于斜边的平方.在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派.
中国古代称直角三角形为勾股形(直角边中较小者为勾,另一长直角边为股,斜边为弦),周朝时期的商高提出了“勾三股四弦五”的特例,所以我国称这个定理为勾股定理,也有人称商高定理.
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。下面是小明搜集到的勾股定理的一种证明方法(不完整).
如图,在中, , , , .
求证: .
证明:作出的外接圆O.延长到点D,使得 . 连接 , 交于点E.延长与的延长线交于点M.连接 , 延长与交于点N
∵ , ∴ , 为的直径.
∴ . (依据1)
∴ ,
…

学习任务:
(1)、材料中“依据1”是:;(2)、请根据上述材料中的部分证明过程,判断与的数量关系和位置关系,并证明;(3)、请结合材料与(2)中的证明过程,用不同的方法表示图中阴影部分面积,完成勾股定理的证明(用含a,b,c的式子表示).30. 设 , 是两个不相等的正整数,为质数,满足 , 且是整数.(1)、求证:;(2)、求的值;(3)、求 , 的值.31. 在小学,我们学习过能被3整除的数的规律,其实这个结论可以用因式分解的方法证明.(1)、请你判断111222(填能或不能)被3整除;(2)、为什么可以用各数位上的数字之和判断一个数能不能被3整除呢?小明先选了一个能被3整除的四位数“1236”试着进行推理:;
∵“”能被3整除,
∴当“”被3整除,原数就能被3整除.
现在,设是个四位数,其个位、十位、百位、千位上的数字分别是d,c,b,a,请你借鉴小明的思路,证明:若“”能被3整除,则能被3整除;
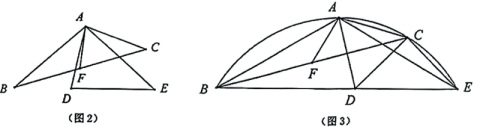
(3)、定义:一个自然数按从右往左的第1、3、5、7、…数位,我们称为奇位,按从右往左的第2、4、6、8、…数位,我们称为偶位.例如:一个四位数,其个位与百位即奇位,十位与千位为偶位.奇位和就是把所有位于奇位上的数字相加,偶位和就是把所有位于偶位上的数字相加.请证明,若的偶位和与奇位和的差是11的倍数,则能被11整除.32. 如果两个三角形的两边对应相等,且它们的夹角互补,那么这两个三角形叫做互补三角形.如图1,的中线,则和就是互补三角形.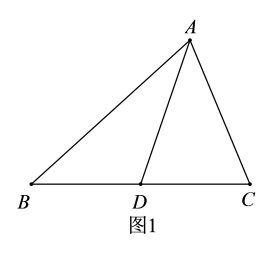
 (1)、根据定义判断下面两个命题的真假(填“真”或“假”)
(1)、根据定义判断下面两个命题的真假(填“真”或“假”)①互补三角形一定不全等.命题
②互补三角形的面积相等.命题
(2)、如图2,和为互补三角形,是的中线.求证:;
(3)、如图3,在(2)的条件下,若三点共线,连结CE, , 四边形为圆内接四边形.当时,求的值.33. 已知,如图1,Rt△ABC中,AB=AC,∠BAC=90°,D为△ABC外一点,且∠ADC=90°,E为BC中点,AF∥BC,连接EF交AD于点G,且EF⊥ED交AC于点H,AF=1. (1)、若 , 求EF的长;(2)、在(1)的条件下,求CD的值;(3)、如图2,连接BD,BG,若BD=AC,求证:BG⊥AD.
(1)、若 , 求EF的长;(2)、在(1)的条件下,求CD的值;(3)、如图2,连接BD,BG,若BD=AC,求证:BG⊥AD.五、实践探究题
-
34. 阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末n位能被 整除的数,本身必能被 整除,反过来,末n位不能被 整除的数,本身也不可能被 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
, 为整数, 能被25整除
, 不为整数, 不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)、若 这个三位数能被11整除,则 ▲;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数.(2)、若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.35. 如图 (1)、阅读理解:
(1)、阅读理解:我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度=PQ= QR = RS,(这个条件很重要哦!)勾 尺的一边 MN 满足M, N, Q三点共线(所以PQ ⊥ MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE //BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP:
请完成第三步操作,图中∠ABC的三等分线是射线、.
(2)、在(1)的条件下补全三等分∠ABC的主要证明过程:∵ , BQ⊥PR,
∴BP= BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠RBQ=∠PBQ,
∵PT⊥BC,PQ⊥BQ,PT=PQ,
∴∠= ∠. (角的内部到角的两边距离相等的点在角的平分线上)
∴∠ == ∠= ∠
(3)、在(1)的条件下探究:∠ABS= ∠ABC是否成立?如果成立,请说明理由;如果不成立,请在下图中∠ABC外部画出∠ABV = ∠ABC(无需写画法,保留画图痕迹即可)