中考数学第一轮复习:圆
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 如图,A , B , C是上的三点,若 , 则的度数是( )
 A、 B、 C、 D、2. 在同一平面内,已知的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是( )A、2 B、5 C、6 D、83. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
A、 B、 C、 D、2. 在同一平面内,已知的半径为2,圆心O到直线l的距离为3,点P为圆上的一个动点,则点P到直线l的最大距离是( )A、2 B、5 C、6 D、83. 如图,点 , , , 均在直线上,点在直线外,则经过其中任意三个点,最多可画出圆的个数为( )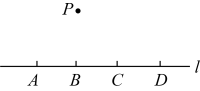 A、3个 B、4个 C、5个 D、6个4. 如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I为三个角的平分线的交点,若∠BOC的度为x,∠BIC的度数为y,则x、y之间的数量关系是( )
A、3个 B、4个 C、5个 D、6个4. 如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I为三个角的平分线的交点,若∠BOC的度为x,∠BIC的度数为y,则x、y之间的数量关系是( ) A、x+y=90° B、x-2y=90° C、x+180°=2y D、4y-x=360°5. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( )
A、x+y=90° B、x-2y=90° C、x+180°=2y D、4y-x=360°5. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( ) A、8 B、4 C、3.5 D、36. 如图,四边形内接于 , 的半径为 , , 则的长是( )
A、8 B、4 C、3.5 D、36. 如图,四边形内接于 , 的半径为 , , 则的长是( )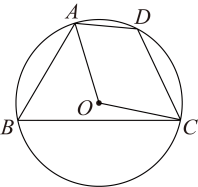 A、 B、 C、 D、7. 已知一个正多边形的每个外角等于45°,则这个正多边形是( )A、正五边形 B、正六边形 C、正七边形 D、正八边形8. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )
A、 B、 C、 D、7. 已知一个正多边形的每个外角等于45°,则这个正多边形是( )A、正五边形 B、正六边形 C、正七边形 D、正八边形8. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )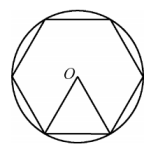 A、 B、 C、3 D、9. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定10. 如图,点A是上一定点,点B是上一动点、连接、、 , 分别将线段、绕点A顺时针旋转到、 , 连接、、、 , 下列结论:①点在上;②;③;④当时,与相切.正确的有( )
A、 B、 C、3 D、9. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是A、相交 B、相切 C、相离 D、无法确定10. 如图,点A是上一定点,点B是上一动点、连接、、 , 分别将线段、绕点A顺时针旋转到、 , 连接、、、 , 下列结论:①点在上;②;③;④当时,与相切.正确的有( ) A、4个 B、3个 C、2个 D、1个11. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形12. 如图,点A , B , C在上, , 连接 , . 若的半径为3,则扇形(阴影部分)的面积为( )
A、4个 B、3个 C、2个 D、1个11. 在中, , 下列说法错误的是( )A、 B、 C、内切圆的半径 D、当时,是直角三角形12. 如图,点A , B , C在上, , 连接 , . 若的半径为3,则扇形(阴影部分)的面积为( ) A、 B、 C、 D、13. 如图,的直径 , 是弦, , , , 的延长线与的延长线相交于点 , 的延长线与的延长线相交于点 , 连接 . 下列结论中正确的个数是( )
A、 B、 C、 D、13. 如图,的直径 , 是弦, , , , 的延长线与的延长线相交于点 , 的延长线与的延长线相交于点 , 连接 . 下列结论中正确的个数是( )①;
②是的切线;
③B,E两点间的距离是;
④ .
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
14. 如图,在半径为3的中,点A是劣弧的中点,点D是优弧上一点,且 , 则的长度是 .
 15. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , .
15. 如图,线段是的直径,弦于点H,点是弧上任意一点(不与B,C重合), , .延长线段交的延长线于点E,直线交于点N,连结交于点F,则 , . 16. 生活中,我们所见到的地面常常是由一种或几种形状相同的图形拼接而成的.如图所示是由一块正三角形瓷砖与三块相同的正n边形瓷砖拼成的无缝隙、不重叠的地面的一部分,则n的值为 .
16. 生活中,我们所见到的地面常常是由一种或几种形状相同的图形拼接而成的.如图所示是由一块正三角形瓷砖与三块相同的正n边形瓷砖拼成的无缝隙、不重叠的地面的一部分,则n的值为 . 17. 半径为的圆内接正五边形一边所对劣弧的长为 .18. 小明对《数书九章》中的“遥度圆城”问题进行了改编:如图,一座圆形城堡有正东、正南、正西和正北四个门,出南门向东走一段路程后刚好看到北门外的一颗大树,向树的方向走9里到达城堡边,再往前走6里到达树下.则该城堡的外围直径为里.
17. 半径为的圆内接正五边形一边所对劣弧的长为 .18. 小明对《数书九章》中的“遥度圆城”问题进行了改编:如图,一座圆形城堡有正东、正南、正西和正北四个门,出南门向东走一段路程后刚好看到北门外的一颗大树,向树的方向走9里到达城堡边,再往前走6里到达树下.则该城堡的外围直径为里. 19. 已知的半径为 , 的半径为 , 圆心距 , 如果在上存在一点 , 使得 , 则的取值范围是 .20. 如图,是的切线,为切点,的延长线交于点,连接 , 如果 , , 那么的长等于 .
19. 已知的半径为 , 的半径为 , 圆心距 , 如果在上存在一点 , 使得 , 则的取值范围是 .20. 如图,是的切线,为切点,的延长线交于点,连接 , 如果 , , 那么的长等于 .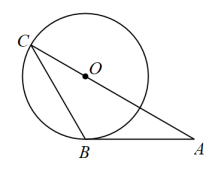 21. 已知相交两圆的半径长分别为13和20,公共弦的长为24,那么这两个圆的圆心距为 .22. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.23. 若圆锥的底面半径是2,侧面展开图是一个圆心角为120的扇形,则该圆锥的母线长是 .24. 如图,一个圆桶底面直径为5cm,高12cm,则桶内所能容下的最长木棒为cm.
21. 已知相交两圆的半径长分别为13和20,公共弦的长为24,那么这两个圆的圆心距为 .22. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.23. 若圆锥的底面半径是2,侧面展开图是一个圆心角为120的扇形,则该圆锥的母线长是 .24. 如图,一个圆桶底面直径为5cm,高12cm,则桶内所能容下的最长木棒为cm.
三、解答题
-
25. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 .
 (1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.26. 已知内接于 , 为的直径,N为的中点,连接交于点H .
(1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.26. 已知内接于 , 为的直径,N为的中点,连接交于点H .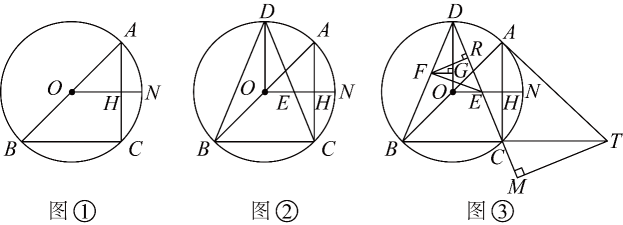 (1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.
(1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.四、综合题
-
27. 如图,O为坐标原点,一次函数的图象与x轴、y轴分别相交于A、B两点,半径为2的经过A、B两点.
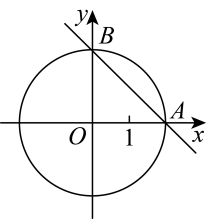 (1)、写出A、B两点的坐标;(2)、求此一次函数的解析式;(3)、求圆心O到直线的距离.28. 如图,已知是的直径,直线是的切线,切点为 , , 垂足为 . 连接 .
(1)、写出A、B两点的坐标;(2)、求此一次函数的解析式;(3)、求圆心O到直线的距离.28. 如图,已知是的直径,直线是的切线,切点为 , , 垂足为 . 连接 . (1)、求证:平分;(2)、若 , , 求的半径.29. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , .
(1)、求证:平分;(2)、若 , , 求的半径.29. 如图,是的直径,是上一点过点作于点 , 交于点 , 点是延长线上一点,连接 , , . (1)、求证:是切线;(2)、若 , , 求的长.30. 如图,内接于⊙ , ⊙的直径AD与弦BC相交于点E,BE=CE,过点D作交AC的延长线于点F.
(1)、求证:是切线;(2)、若 , , 求的长.30. 如图,内接于⊙ , ⊙的直径AD与弦BC相交于点E,BE=CE,过点D作交AC的延长线于点F. (1)、求证:DF是⊙的切线;(2)、若 , AB=6,求DF的长.31. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题:
(1)、求证:DF是⊙的切线;(2)、若 , AB=6,求DF的长.31. 如图,在单位长度为1的网格中,点O,A,B均在格点上, , , 以O为圆心,为半径画圆,请按下列步骤完成作图,并回答问题: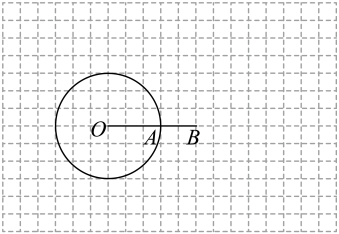
①过点A作切线 , 且(点C在A的上方);
②连接 , 交于点D;
③连接 , 与交于点E.
(1)、求证:为的切线;(2)、求的长度.32. 如图,在平面直角坐标系 中,抛物线 与x轴相交于点 , ,与y轴交于点C.将抛物线的对称轴沿x轴的正方向平移,平移后交x轴于点D , 交线段 于点E , 交抛物线于点F , 过点F作直线 的垂线,垂足为点G. (1)、求抛物线的表达式;(2)、以点G为圆心, 为半径画 ;以点E为圆心, 为半径画 .当 与 内切时.
(1)、求抛物线的表达式;(2)、以点G为圆心, 为半径画 ;以点E为圆心, 为半径画 .当 与 内切时.①试证明 与 的数量关系;
②求点F的坐标.
33. 梯形中, , 于点 , , , 以为直径,以为直径,直线与交于点 , 与交于点(如图),设 .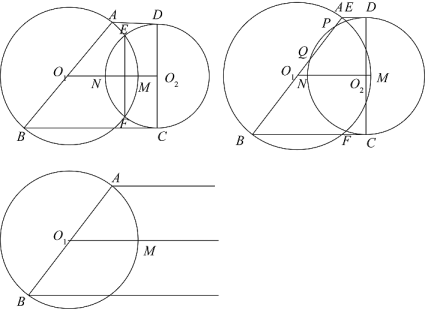 (1)、记两圆交点为、(在上方),当时,求的值;(2)、当与线段交于、时,设 , 求关于的函数关系式,并写出定义域;(3)、连接 , 线段与交于点 , 分别连接、 , 若与相似,求的值.34. 如图 , 在正方形中,是边上的动点,在的外接圆上,且位于正方形的内部, , 连结 , .
(1)、记两圆交点为、(在上方),当时,求的值;(2)、当与线段交于、时,设 , 求关于的函数关系式,并写出定义域;(3)、连接 , 线段与交于点 , 分别连接、 , 若与相似,求的值.34. 如图 , 在正方形中,是边上的动点,在的外接圆上,且位于正方形的内部, , 连结 , . (1)、求证:是等腰直角三角形;(2)、如图 , 连结 , 过点作于点 , 请探究线段与的数量关系,并说明理由;(3)、当点是的中点时, .
(1)、求证:是等腰直角三角形;(2)、如图 , 连结 , 过点作于点 , 请探究线段与的数量关系,并说明理由;(3)、当点是的中点时, .①求的长;
②若点是外接圆上的动点,且位于正方形的外部,连结当与的一个内角相等时,求所有满足条件的的长.
五、实践探究题
-
35.
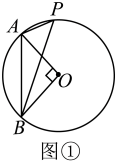
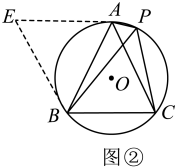
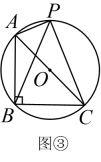 (1)、【感知】如图①,点A、B、P均在上, , 则锐角的大小为度.(2)、【探究】小明遇到这样一个问题:如图②,是等边三角形的外接圆,点P在上(点P不与点A、C重合),连结、、 . 求证: . 小明发现,延长至点E,使 , 连结 , 通过证明 , 可推得是等边三角形,进而得证.
(1)、【感知】如图①,点A、B、P均在上, , 则锐角的大小为度.(2)、【探究】小明遇到这样一个问题:如图②,是等边三角形的外接圆,点P在上(点P不与点A、C重合),连结、、 . 求证: . 小明发现,延长至点E,使 , 连结 , 通过证明 , 可推得是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长至点E,使 , 连结 ,
四边形是的内接四边形,
.
,
.
是等边三角形.
,
请你补全余下的证明过程.
(3)、【应用】如图③,是的外接圆, , 点P在上,且点P与点B在的两侧,连结、、 . 若 , 则的值为 .36. 【定义】从一个已知图形的外一点引两条射线分别经过该已知图形的两点,则这两条射线所成的最大角称为该点对已知图形的视角,如图①,是点P对线段的视角.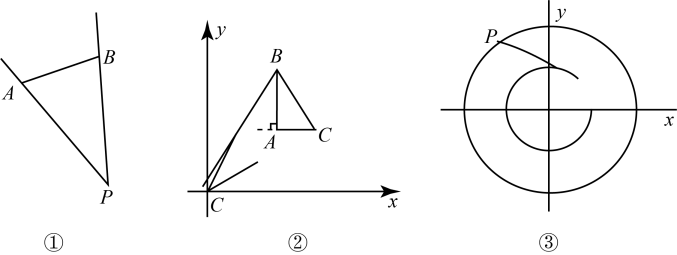 (1)、【应用】
(1)、【应用】
如图②,在直角坐标系中,已知点 , , , 则原点O对三角形的视角为;(2)、如图③,在直角坐标系中,以原点O,半径为2画圆 , 以原点O,半径为4画圆 , 证明:圆上任意一点P对圆的视角是定值;(3)、【拓展应用】
很多摄影爱好者喜欢在天桥上对城市的标志性建筑拍照,如图④.现在有一条笔直的天桥,标志性建筑外延呈正方形,摄影师想在天桥上找到对建筑视角为的位置拍摄.现以建筑的中心为原点建立如图⑤的坐标系,此时天桥所在的直线的表达式为 , 正方形建筑的边长为4,请直接写出直线上满足条件的位置坐标.