中考数学第一轮复习:四边形
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 已知AB∥CD,AD∥BC,则四边形ABCD是( )A、平行四边形 B、矩形 C、菱形 D、正方形2. 如图,在中, , 且分别是上的高,分别是的中点,若 , 则的长为( )
 A、10 B、12 C、13 D、143. 下列叙述错误的是( )A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、对角线互相平分的四边形是平行四边形 D、对角线相等的四边形是矩形4. 如图,在正方形的外侧作等边三角形 , 则度数为( )
A、10 B、12 C、13 D、143. 下列叙述错误的是( )A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、对角线互相平分的四边形是平行四边形 D、对角线相等的四边形是矩形4. 如图,在正方形的外侧作等边三角形 , 则度数为( ) A、 B、 C、 D、5. 在四边形中, . 如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )A、 B、 C、 D、6. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( )
A、 B、 C、 D、5. 在四边形中, . 如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )A、 B、 C、 D、6. 如图,在矩形ABCD中,.把AD沿AE折叠,使点恰好落在AB边上的处,再将绕点顺时针旋转 , 得到 , 使得恰好经过的中点.设交AB于点 , 连接.有如下结论:①;②的长度是;③;④.上述结论中,正确的个数有( ) A、1个 B、2个 C、3个 D、4个7. 下列说法正确的个数有( )
A、1个 B、2个 C、3个 D、4个7. 下列说法正确的个数有( )①若直角梯形的上底和中位线的长确定,则下底的长唯一确定②两条对角线相等的四边形一定是等腰梯形③梯形可以分为直角梯形和等腰梯形④等腰梯形是轴对称图形,它的对称轴是连接两底中点的直线
A、个 B、个 C、个 D、个8. 如图,四边形中, , . 点从点A出发,以的速度向点D运动;点从点C同时出发,以的速度向点B运动.规定其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为秒,下列结论错误的是( ) A、当时, B、当时, C、当或时, D、当时,四边形的最大面积为9. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )
A、当时, B、当时, C、当或时, D、当时,四边形的最大面积为9. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )①;②;③;④;⑤
 A、2个 B、3个 C、4个 D、5个10. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( )
A、2个 B、3个 C、4个 D、5个10. 如图,在中, , , 、分别为、中点,连接、相交于点 , 点在上,且:: , 则四边形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 过七边形一个顶点可以引出的对角线的条数为 .12. 正多边形的一个内角是108°,则这个多边形的边数是.13. 图形的密铺(或称图形的镶嵌)指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间既不留空隙、也不互相重叠地把一部分平面完全覆盖.图1所示的是一种五边形密铺的结构图,图2是从该密铺图案中抽象出的一个五边形,其中 , , 则的度数是 .
 14. 如图,在中,AD为BC边上的中线,若与的周长差为3, , 则 .
14. 如图,在中,AD为BC边上的中线,若与的周长差为3, , 则 . 15. 如图,矩形中,点O、M分别是、的中点, , , 则的长为 .
15. 如图,矩形中,点O、M分别是、的中点, , , 则的长为 . 16. 我们把两条对角线长度之比为的菱形叫做“钻石菱形”,如果一个“钻石菱形”的面积为8,那么它的边长是 .17. 如图,直角 , 沿着点B到C点的方向平移到的位置, , , 若阴影部分的面积是42.5,则平移距离为 .
16. 我们把两条对角线长度之比为的菱形叫做“钻石菱形”,如果一个“钻石菱形”的面积为8,那么它的边长是 .17. 如图,直角 , 沿着点B到C点的方向平移到的位置, , , 若阴影部分的面积是42.5,则平移距离为 .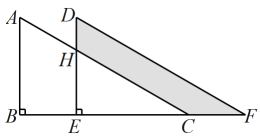 18. 已知在等腰梯形中, , , 垂足为点O,如果 , 那么梯形的上下底之和等于 .
18. 已知在等腰梯形中, , , 垂足为点O,如果 , 那么梯形的上下底之和等于 .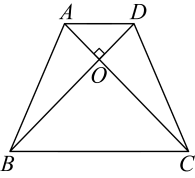 19. 如图,在平行四边形中, , , , 则平行四边形的面积为 .
19. 如图,在平行四边形中, , , , 则平行四边形的面积为 .
三、解答题
-
20. 如图,在中,对角线相交于点 , 垂足分别为 . 求证:
 (1)、;(2)、 .21. 如图,是平行四边形中边延长线的上一点,连接 , , . 若 , 求证:四边形为平行四边形.
(1)、;(2)、 .21. 如图,是平行四边形中边延长线的上一点,连接 , , . 若 , 求证:四边形为平行四边形. 22. 在长方形中, , , 点是边上的一点,将沿折叠,点的对应点为点 , 射线与线段交于点 .
22. 在长方形中, , , 点是边上的一点,将沿折叠,点的对应点为点 , 射线与线段交于点 . (1)、如图1,当点和点重合时,求证:;(2)、如图2,连接 , , 若 , 求的面积.23. 如图,在中, , 过上一点作交于点 , 以为顶点,为一边,作 , 另一边交于点
(1)、如图1,当点和点重合时,求证:;(2)、如图2,连接 , , 若 , 求的面积.23. 如图,在中, , 过上一点作交于点 , 以为顶点,为一边,作 , 另一边交于点 (1)、求证:四边形是平行四边形;(2)、延长图①中的到点 , 使 , 连接 , , , 得到图②,若 , 判断四边形的形状,并说明理由.24. 如图1,在矩形纸片中, , , 折叠纸片使点落在上的点处,折痕为 , 过点作EF//AB交于点.
(1)、求证:四边形是平行四边形;(2)、延长图①中的到点 , 使 , 连接 , , , 得到图②,若 , 判断四边形的形状,并说明理由.24. 如图1,在矩形纸片中, , , 折叠纸片使点落在上的点处,折痕为 , 过点作EF//AB交于点.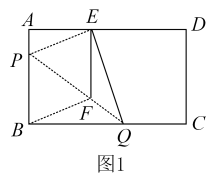
 (1)、求证:四边形为菱形;(2)、当折痕的点与点重合时(如图2),求菱形的边长.25. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F在线段BD上,且 , 连结AE、CE、AF、CF.
(1)、求证:四边形为菱形;(2)、当折痕的点与点重合时(如图2),求菱形的边长.25. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F在线段BD上,且 , 连结AE、CE、AF、CF. (1)、求证:四边形AECF为平行四边形;(2)、若 , , , 求四边形AECF的周长.26. 如图,过点C在正方形的外部作直线 , 点D关于直线的对称点为 , 连接交直线于点G,过点B作交直线于点F,连接交直线于点E.
(1)、求证:四边形AECF为平行四边形;(2)、若 , , , 求四边形AECF的周长.26. 如图,过点C在正方形的外部作直线 , 点D关于直线的对称点为 , 连接交直线于点G,过点B作交直线于点F,连接交直线于点E. (1)、求证: .(2)、求证:(3)、若 , 求的长.27. 如图,菱形的对角线 , 相交于点 , 在上截取 , 顺次连接 , , , 四点.求证:四边形是正方形,
(1)、求证: .(2)、求证:(3)、若 , 求的长.27. 如图,菱形的对角线 , 相交于点 , 在上截取 , 顺次连接 , , , 四点.求证:四边形是正方形, 28. 如图,已知平行四边形中,对角线交点O,E是延长线上的点,且是等边三角形.
28. 如图,已知平行四边形中,对角线交点O,E是延长线上的点,且是等边三角形. (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.29. 如图,已知是等边三角形,过点作(),且 , 连接、 .
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.29. 如图,已知是等边三角形,过点作(),且 , 连接、 . (1)、求证:四边形是等腰梯形;(2)、点在腰上,连接交于点 , 若 , 求证: .30. 如图,在正方形中,线段绕点C逆时针旋转到处,旋转角为 , 点F在直线上,且 , 连接 .
(1)、求证:四边形是等腰梯形;(2)、点在腰上,连接交于点 , 若 , 求证: .30. 如图,在正方形中,线段绕点C逆时针旋转到处,旋转角为 , 点F在直线上,且 , 连接 . (1)、如图1,当时,
(1)、如图1,当时,①求的大小(用含的式子表示).
②求证: .
(2)、如图2,取线段的中点G , 连接 , 已知 , 请直接写出在线段旋转过程中()面积的最大值.31. 如图,点E在正方形内,且满足 , , , 求图中阴影部分的面积.
四、综合题
-
32. 如图

 (1)、如图所示,小迪用四根长度分别为a,b,c,d的木条和直角尺按照如示搭了一个四边形木框,搭出的木框(木框的宽度忽略不计)的形状是;(2)、用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是.33. 已知:如图,平行四边形的对角线相交于点O, , , 且 .
(1)、如图所示,小迪用四根长度分别为a,b,c,d的木条和直角尺按照如示搭了一个四边形木框,搭出的木框(木框的宽度忽略不计)的形状是;(2)、用(1)中的四根木条重新组合,搭出(1)中形状的木框的最大面积是.33. 已知:如图,平行四边形的对角线相交于点O, , , 且 . (1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.(3)、在(2)的条件下,若点F为边上的一个动点,点F到与的距离之和为a,则 . (直接写出答案)34. 如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,表格列举的是直线l上的点的取值情况.
(1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.(3)、在(2)的条件下,若点F为边上的一个动点,点F到与的距离之和为a,则 . (直接写出答案)34. 如图,在平面直角坐标系中,直线l交x轴于点A,交y轴于点B,表格列举的是直线l上的点的取值情况.x
…
0
1
2
3
4
5
…
y
…
5
4
3
2
1
0
…
 (1)、观察表格,直接写出直线l上的点的横坐标x与纵坐标y之间的数量关系为;(2)、若点在第一象限,且满足的面积为6,求点的横、纵坐标满足的数量关系;(3)、在(2)的条件下,直线与直线相交于点D,若三角形的面积不大于三角形的面积,求点的横坐标m的取值范围.
(1)、观察表格,直接写出直线l上的点的横坐标x与纵坐标y之间的数量关系为;(2)、若点在第一象限,且满足的面积为6,求点的横、纵坐标满足的数量关系;(3)、在(2)的条件下,直线与直线相交于点D,若三角形的面积不大于三角形的面积,求点的横坐标m的取值范围.

