中考数学第一轮复习:三角形综合
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 如图,在矩形中, , 对角线与相交于点O,于E,若 , 则的长是( )
 A、 B、 C、2 D、32. 如图,在正方形网格中,网格线的交点称为格点.已知A , B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A、 B、 C、2 D、32. 如图,在正方形网格中,网格线的交点称为格点.已知A , B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( ) A、6 B、7 C、8 D、93. 如图,在▱ABCD中,AE⊥BC,AF⊥CD,∠EAF=45°,且AE=AF= , 则平行四边形ABCD的周长是( )
A、6 B、7 C、8 D、93. 如图,在▱ABCD中,AE⊥BC,AF⊥CD,∠EAF=45°,且AE=AF= , 则平行四边形ABCD的周长是( ) A、 B、 C、 D、84. 已知菱形的对角线的长度恰为方程的两个实数根,则菱形的周长为( )A、12 B、16 C、20 D、245. 如图,在中, , 在同一平面内,将绕点逆时针方向旋转到 , 点恰好落在边的延长线上,则( )
A、 B、 C、 D、84. 已知菱形的对角线的长度恰为方程的两个实数根,则菱形的周长为( )A、12 B、16 C、20 D、245. 如图,在中, , 在同一平面内,将绕点逆时针方向旋转到 , 点恰好落在边的延长线上,则( )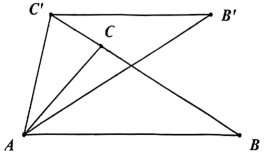 A、 B、 C、 D、6. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( )
A、 B、 C、 D、6. 如图,在中,对角线、相交于点 , 平分 , 分别交、于点、 , 连接 , , , 则下列结论:① , ② , ③ , ④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个7. 如果正整数a、b、c满足等式 , 那么正整数a、b、c叫做勾股数.某同学将自探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
A、1个 B、2个 C、3个 D、4个7. 如果正整数a、b、c满足等式 , 那么正整数a、b、c叫做勾股数.某同学将自探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )a
b
c
3
4
5
8
6
10
15
8
17
24
10
26
…
…
…
x
14
y
A、67 B、34 C、98 D、738. 如图, , 在射线 , 上分别截取 , 连接 , 的平分线交于点D , 点E为线段上的动点,作交于点F , 作交射线于点G , 过点G作于点H , 点E沿方向运动,当点E与点B重合时停止运动.设点E运动的路程为x , 四边形与重叠部分的面积为S , 则能大致反映S与x之间函数关系的图象是( )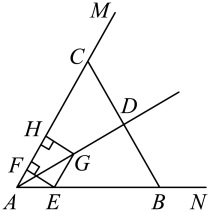 A、
A、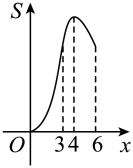 B、
B、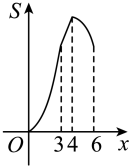 C、
C、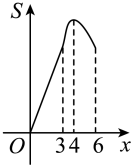 D、
D、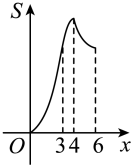 9. 如图,在△ABC中, , , , △ABD , △ACE , △BCF都是等边三角形,下列结论中:①;②四边形AEFD是平行四边形;③;④ . 正确的个数是( )
9. 如图,在△ABC中, , , , △ABD , △ACE , △BCF都是等边三角形,下列结论中:①;②四边形AEFD是平行四边形;③;④ . 正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )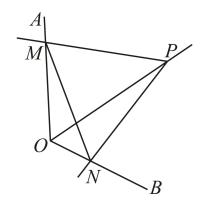 A、的值不变 B、 C、的长不变 D、四边形的面积不变
A、的值不变 B、 C、的长不变 D、四边形的面积不变二、填空题
-
11. 如图,在等腰梯形中, , 对角线 , , , 则梯形的面积为 .
 12. 矩形的对角线 , 相交于 , , , 则 .13. 在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.3世纪,汉代赵爽在注解《周髀算经》时,通过对图形的切割、拼接、巧妙地利用面积关系证明了勾股定理:直角三角形的两条直角边的平方和等于斜边的平方.在△ABC中,∠C=90°,斜边AB=13,AC=12,则BC的长度为.14. 我国汉代数学家赵爽证明勾股定理时创制了“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成,如图,直角三角形的直角边长为a,b,斜边长为c,若 , 每个直角三角形的面积为15,则c的长为 .
12. 矩形的对角线 , 相交于 , , , 则 .13. 在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.3世纪,汉代赵爽在注解《周髀算经》时,通过对图形的切割、拼接、巧妙地利用面积关系证明了勾股定理:直角三角形的两条直角边的平方和等于斜边的平方.在△ABC中,∠C=90°,斜边AB=13,AC=12,则BC的长度为.14. 我国汉代数学家赵爽证明勾股定理时创制了“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成,如图,直角三角形的直角边长为a,b,斜边长为c,若 , 每个直角三角形的面积为15,则c的长为 . 15. 在中, , , 的对边分别是 , , , 下列条件:①与互余;②;③ , 其中可以判定是直角三角形的有个.16. 如图是一个三级台阶,每一级的长,宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,若一只壁虎从A点出发沿着台阶面爬到B点,则壁虎爬行的最短路线的长是 .
15. 在中, , , 的对边分别是 , , , 下列条件:①与互余;②;③ , 其中可以判定是直角三角形的有个.16. 如图是一个三级台阶,每一级的长,宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,若一只壁虎从A点出发沿着台阶面爬到B点,则壁虎爬行的最短路线的长是 . 17. 如图, , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动.它们运动的时间为 . 当与全等时,的值为 .
17. 如图, , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动.它们运动的时间为 . 当与全等时,的值为 . 18. 如图,在中,将绕点A顺时针旋转至 , 将绕点A逆时针旋转至 , 得到 , 使 , 我们称是的“旋补三角形”,的中线叫做的“旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .
18. 如图,在中,将绕点A顺时针旋转至 , 将绕点A逆时针旋转至 , 得到 , 使 , 我们称是的“旋补三角形”,的中线叫做的“旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .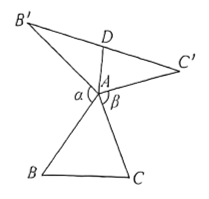
①与面积相同;
②;
③若 , 连接和 , 则;
④若 , , , 则 .
19. 在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A , C重合),且∠ABP=30°,则CP的长为 .20. 如图,一次函数的图象过点 , 且与x轴相交于点B . 若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是 .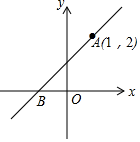 21. 如图,在矩形中, , 将矩形绕点B旋转一定角度后得矩形 , 交于点E,且 , 则的长为 .
21. 如图,在矩形中, , 将矩形绕点B旋转一定角度后得矩形 , 交于点E,且 , 则的长为 . 22. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
22. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
三、作图题
-
23. 如图,已知△ABC,∠C=90°,∠A=30°,用尺规作图法在AC上确定一点P,使PB+PC=AC.(不写作法,保留作图痕迹.)

四、解答题
-
24. 如图,与相交于点O , , , , 连接 , 求证;垂直平分 .
 25. 如图,在中,点E在上,点F在上,且 .
25. 如图,在中,点E在上,点F在上,且 .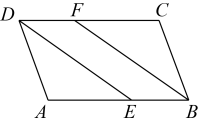 (1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.26. 在中,、分别是、的中点,连接、 .
(1)、求证:四边形是平行四边形;(2)、若为的平分线,且 , , 求的周长.26. 在中,、分别是、的中点,连接、 .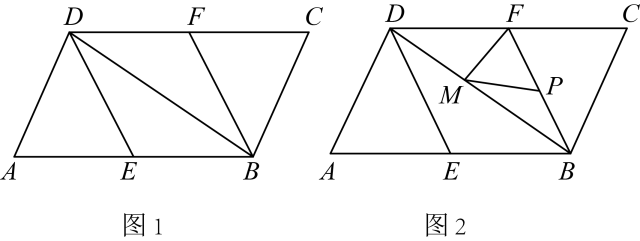 (1)、求证:;(2)、如图 , 当满足什么条件时,四边形是菱形,并说明理由;(3)、如图 , 为的中点,是线段上一动点,在(2)的条件下,若 , , 求的最小值.27. 已知:如图,在▱ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)、求证:;(2)、如图 , 当满足什么条件时,四边形是菱形,并说明理由;(3)、如图 , 为的中点,是线段上一动点,在(2)的条件下,若 , , 求的最小值.27. 已知:如图,在▱ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G. (1)、求证:AE⊥DF;(2)、若AD=10,AB=6,AE=4,求DF的长.28. 如图,在菱形中,对角线 , 相交于点 , 延长到点 , 使得 . 连接 . 过点作 , 交于点 , 连接 .
(1)、求证:AE⊥DF;(2)、若AD=10,AB=6,AE=4,求DF的长.28. 如图,在菱形中,对角线 , 相交于点 , 延长到点 , 使得 . 连接 . 过点作 , 交于点 , 连接 . (1)、求证:四边形是矩形;(2)、若 , , 求的长.29. 在矩形中, , , E、F是直线上的两个动点,分别从A、C两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为t秒,其中 .
(1)、求证:四边形是矩形;(2)、若 , , 求的长.29. 在矩形中, , , E、F是直线上的两个动点,分别从A、C两点同时出发相向而行,速度均为每秒2个单位长度,运动时间为t秒,其中 .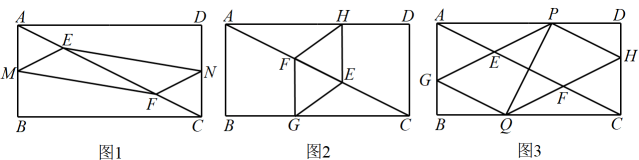 (1)、如图1,M、N分别是中点,当四边形是矩形时,求t的值;(2)、若G、H分别从点A、C沿折线 , 运动,与相同的速度同时出发.
(1)、如图1,M、N分别是中点,当四边形是矩形时,求t的值;(2)、若G、H分别从点A、C沿折线 , 运动,与相同的速度同时出发.①如图2,若四边形为菱形,求t的值;
②如图3,作的垂直平分线交于点P、Q,当四边形的面积是矩形面积的时,则t的值是 ▲ .
五、综合题
-
30. 如图
 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.31. 如图,在中, , , . 动点P从点A出发,沿着A→C→B→A的路径,以每秒的速度运动,当P回到A点时运动结束,设点P运动的时间为t秒.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= , 其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.31. 如图,在中, , , . 动点P从点A出发,沿着A→C→B→A的路径,以每秒的速度运动,当P回到A点时运动结束,设点P运动的时间为t秒. (1)、当时,求的面积;(2)、若平分 , 求t的值;(3)、深入探索:若点P运动到边 , 且是等腰三角形,求t的值.32. 如图,在等腰中, , , 点D是直线上一动点,以为边,在下方作等边 .
(1)、当时,求的面积;(2)、若平分 , 求t的值;(3)、深入探索:若点P运动到边 , 且是等腰三角形,求t的值.32. 如图,在等腰中, , , 点D是直线上一动点,以为边,在下方作等边 . (1)、直接写出的长,;(2)、当点D从点B运动到点C时,求点E的运动路径长;(3)、当时,求出的值.
(1)、直接写出的长,;(2)、当点D从点B运动到点C时,求点E的运动路径长;(3)、当时,求出的值.六、实践探究题
-
33. 在平面直角坐标系中,已知点 , , 根据勾股定理,我们可以求得这两个这点间的距离 . 当点在坐标轴上或平行(垂直)于坐标轴的直线上时,两点间的距离可简化为 , 或 .
请利用以上结论,回答下列问题:
(1)、已知 , , 则两点间的距离为;(2)、已知在平行于轴的直线上,点的横坐标为5,点的横坐标为-2,则点两之间的距离为;(3)、已知一个三角形各顶点的坐标为 , , , 请判定此三角形的形状,并说明理由.34.(1)、问题提出在平面内,已知线段 , , 则线段的最小值为 .
(2)、问题探究如图1,在平行四边形中, , , , P是边的中点,Q是边上一动点,将三角形沿所在直线翻折,得到三角形 , 连接 , 求的最小值.
(3)、问题解决如图2,平行四边形为某公园平面示意图,扇形为该公园的人口广场,已知 , , , . 为了提升游客体验感,工作人员准备在弧上找一点P , 沿 , 修两条绿色通道,并在上方和右方区域种植花卉供游客观赏,其余地方修建其他设施,求其他设施区域面积的最小值.
 35. 综合与实践
35. 综合与实践问题情境:在数学活动课上,数学老师让同学们用一张矩形纸片进行探究活动.
小亮准备了矩形纸片 , 其中是的中点,将沿折叠,点的对应点为 .
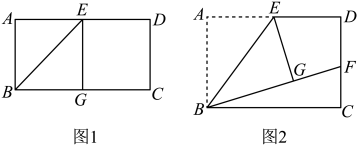 (1)、观察发现:如图1,当点恰好在边上时,小亮发现与存在一定的数量关系,其数量关系是 .(2)、探索猜想:如图2,当点在矩形内部时,延长交边于点 . 试猜想线段与之间的数量关系,并说明理由.(3)、拓展延伸:当点在矩形内部时,若 , 直接写出线段与的数量关系.
(1)、观察发现:如图1,当点恰好在边上时,小亮发现与存在一定的数量关系,其数量关系是 .(2)、探索猜想:如图2,当点在矩形内部时,延长交边于点 . 试猜想线段与之间的数量关系,并说明理由.(3)、拓展延伸:当点在矩形内部时,若 , 直接写出线段与的数量关系.
-