中考数学第一轮复习:二次函数
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 下列函数中,是二次函数的是( )A、 B、 C、 D、2. 对于抛物线 , 下列判断正确的是( )A、抛物线的开口向上 B、抛物线的顶点坐标是 C、对称轴为直线 D、当时,3. 表中列出的是一个二次函数的自变量x与函数y的几组对应值:
x
…
0
1
3
…
y
…
6
…
下列各选项中,正确的是( )
A、这个函数的最小值为 B、这个函数的图象开口向下 C、这个函数的图象与x轴无交点 D、当时,y的值随x值的增大而增大4. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )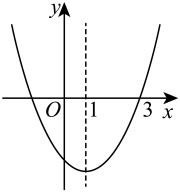 A、 B、 C、 D、点在函数图象上5. 已知二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若点在该函数图象上,则;⑤若方程的两根为和 , 且 , 则 . 其中正确的结论有( )
A、 B、 C、 D、点在函数图象上5. 已知二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:①;②;③;④若点在该函数图象上,则;⑤若方程的两根为和 , 且 , 则 . 其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个6. 二次函数的对称轴是直线( )A、 B、 C、 D、7. 如图,抛物线()的对称轴为直线 , 与x轴的一个交点坐标为( , 0),其部分图象如图所示,下列结论;①;②方程的两个根是 , ;③;④当时,x的取值范围是;⑤当时,y随x增大而增大,其中结论正确的个数是( )
A、2个 B、3个 C、4个 D、5个6. 二次函数的对称轴是直线( )A、 B、 C、 D、7. 如图,抛物线()的对称轴为直线 , 与x轴的一个交点坐标为( , 0),其部分图象如图所示,下列结论;①;②方程的两个根是 , ;③;④当时,x的取值范围是;⑤当时,y随x增大而增大,其中结论正确的个数是( ) A、4个 B、3个 C、2个 D、1个8. 已知二次函数 , 与的部分对应值为:
A、4个 B、3个 C、2个 D、1个8. 已知二次函数 , 与的部分对应值为:-2
-1
0
1
2
-1
2
3
2
?
关于此函数的图象和性质,下列说法正确的是( )
A、当时,函数图象从左到右上升 B、抛物线开口向上 C、方程的一个根在-2与-1之间 D、当时,9. 用总长为a米的材料做成如图所示的矩形窗框,设窗框的宽为x米,窗框的面积为y平方米,y关于x的函数图象如图,则a的值是( ) A、16 B、12 C、8 D、410. 为了使居住环境更加美观,某小区建造了一个小型喷泉,水流从地面上的点O喷出,在各个方向上沿形状相同的抛物线落到地面,某方向上抛物线的形状如图所示,落点A到点O的距离为4,水流喷出的高度与水平距离之间近似满足函数关系式 , 则水流喷出的最大高度为( )
A、16 B、12 C、8 D、410. 为了使居住环境更加美观,某小区建造了一个小型喷泉,水流从地面上的点O喷出,在各个方向上沿形状相同的抛物线落到地面,某方向上抛物线的形状如图所示,落点A到点O的距离为4,水流喷出的高度与水平距离之间近似满足函数关系式 , 则水流喷出的最大高度为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 抛物线的顶点坐标为 .12. 某学校航模组设计制作的火箭升空后离地面的高度与飞行时间满足函数关系式为 . 如果火箭在点火升空到最高点时打开降落伞,那么降落伞将在离地面m处打开.13. 关于的方程的两根均小于 , 则取值范围是.14. 在国家政策的宏观调控下,某市的商品房成交均价由前年的元下降到今年的元 , 则这两年平均每年降价的百分率是 .15. 规定:如果两个函数的图象关于轴对称,那么称这两个函数互为“函数”例如:函数与互为“函数”若函数的图象与轴只有一个交点,则它的“函数”图象与轴的交点坐标为 .
三、作图题
-
16. 已知抛物线上部分点的横坐标与纵坐标的对应值如表所示
…
0
1
2
3
…
…
0
…
 (1)、 ▲ ;并在如图所给的平面直角坐标系中画出该抛物线;(2)、若直线与两坐标轴分别交于点和 , 请直接写出抛物线在直线上方时对应的的取值范围.
(1)、 ▲ ;并在如图所给的平面直角坐标系中画出该抛物线;(2)、若直线与两坐标轴分别交于点和 , 请直接写出抛物线在直线上方时对应的的取值范围.四、解答题
-
17. 如图,抛物线y=2(x-2)2与平行于x轴的直线交于点A,B,抛物线顶点为C,△ABC为等边三角形,求S△ABC;
 18. 如图,在平面直角坐标系中,二次函数的图象与轴交于点和点 , 与y轴交于点C .
18. 如图,在平面直角坐标系中,二次函数的图象与轴交于点和点 , 与y轴交于点C . (1)、求这个二次函数的表达式.(2)、如图1,二次函数图象的对称轴与直线交于点D , 若点M是直线上方抛物线上的一个动点,求面积的最大值.(3)、如图2,点是直线上的一个动点,过点的直线与平行,则在直线上是否存在点 , 使点与点关于直线对称?若存在,请直接写出点的坐标;若不存在,请说明理由.19. 如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米.
(1)、求这个二次函数的表达式.(2)、如图1,二次函数图象的对称轴与直线交于点D , 若点M是直线上方抛物线上的一个动点,求面积的最大值.(3)、如图2,点是直线上的一个动点,过点的直线与平行,则在直线上是否存在点 , 使点与点关于直线对称?若存在,请直接写出点的坐标;若不存在,请说明理由.19. 如图,长为25米,宽为12米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作草地,如果将两条小路铺上地砖,选用地砖的价格是45元/平方米. (1)、写出买地砖需要的费用y(元)与m(米)之间的关系式.(2)、计算当m=2时,买地砖需要的费用.20. 根据以下素材,探索完成任务
(1)、写出买地砖需要的费用y(元)与m(米)之间的关系式.(2)、计算当m=2时,买地砖需要的费用.20. 根据以下素材,探索完成任务如何设计拱桥上救生圈的悬挂方案?
素材1
图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示.
某时测得水面宽 , 拱顶离水面最大距离为10m,抛物线拱形最高点与x轴的距离为5m.据调查,该河段水位在此基础上再涨1m达到最高.

素材2
为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)

问题解决
任务1
确定桥拱形状
根据图2,求抛物线的函数表达式.
任务2
拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3
探究救生绳长度
当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
21. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , , 与轴交于点 .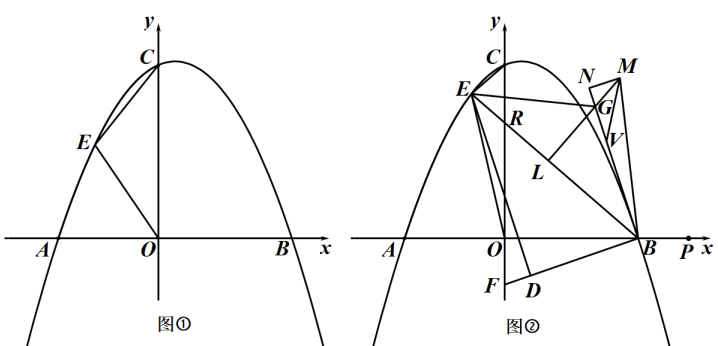 (1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.
(1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.五、综合题
-
22. 在平面直角坐标系中,将二次函数的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与轴交于点、(点在点的左侧), , 经过点的一次函数的图象与轴正半轴交于点 , 且与抛物线的另一个交点为 , 的面积为 .
 (1)、求抛物线和一次函数的解析式;(2)、抛物线上的动点在一次函数的图象下方,当面积的最大值时,求出此时点的坐标;(3)、点是直线上的一动点,连接 , , 设外接圆的圆心为 , 当最大时,求点M的坐标(直接写答案).23. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表:
(1)、求抛物线和一次函数的解析式;(2)、抛物线上的动点在一次函数的图象下方,当面积的最大值时,求出此时点的坐标;(3)、点是直线上的一动点,连接 , , 设外接圆的圆心为 , 当最大时,求点M的坐标(直接写答案).23. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表: (1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.24. 如图,在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C , 且 .
(1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.24. 如图,在平面直角坐标系中,O为坐标原点,抛物线与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C , 且 . (1)、求抛物线的解析式;(2)、如图①,若点P为第一象限的抛物线上一点,直线交x轴于点D , 且平分 , 求点P的坐标;(3)、如图②,点Q为第四象限的抛物线上一点,直线BQ交y轴于点M , 过点B作直线 , 交y轴于点N , 当Q点运动时,线段MN的长度是否会变化?若不变,请求出其长度;若变化,请求出其长度的变化范围.25. 若函数在上的最大值记为 , 最小值记为 , 且满足 , 则称函数是在的“美好函数”.(1)、函数①;②;③ . 其中函数是在上的“美好函数”;(填序号)(2)、已知函数: .
(1)、求抛物线的解析式;(2)、如图①,若点P为第一象限的抛物线上一点,直线交x轴于点D , 且平分 , 求点P的坐标;(3)、如图②,点Q为第四象限的抛物线上一点,直线BQ交y轴于点M , 过点B作直线 , 交y轴于点N , 当Q点运动时,线段MN的长度是否会变化?若不变,请求出其长度;若变化,请求出其长度的变化范围.25. 若函数在上的最大值记为 , 最小值记为 , 且满足 , 则称函数是在的“美好函数”.(1)、函数①;②;③ . 其中函数是在上的“美好函数”;(填序号)(2)、已知函数: .①函数是在上的“美好函数”,求的值;
②当时,函数是在上的“美好函数”,请直接写出的值;
(3)、已知函数: , 若函数是在(为整数)上的“美好函数”,且存在整数 , 使得 , 求的值.26. 已知二次函数(为常数,且).(1)、若点 , 在函数图象上,则 (填“>”、“<”或“=”);(2)、当时, , 则的取值范围是 .27. 已知抛物线(a为常数,)的图象经过原点,点A在抛物线上运动. (1)、求a的值.(2)、若点和点都是这个抛物线上的点,且有 , 求t的取值范围.(3)、设点A位于x轴的下方且在这个抛物线的对称轴的左侧运动,过点A作x轴的平行线交抛物线于另一点D , 过点A作轴,垂足为点B , 过点D作轴,垂足于点C , 试问四边形的周长是否存在最大值?如果存在,请求出这个最大值和对应的x值,如果不存在,请说明理由.28. 已知:在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点 .
(1)、求a的值.(2)、若点和点都是这个抛物线上的点,且有 , 求t的取值范围.(3)、设点A位于x轴的下方且在这个抛物线的对称轴的左侧运动,过点A作x轴的平行线交抛物线于另一点D , 过点A作轴,垂足为点B , 过点D作轴,垂足于点C , 试问四边形的周长是否存在最大值?如果存在,请求出这个最大值和对应的x值,如果不存在,请说明理由.28. 已知:在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点 . (1)、求抛物线的解析式;(2)、如图1,如果把抛物线x轴下方的部分沿x轴翻折 , 抛物线的其余部分保持不变,得到一个新图象.当平面内的直线与新图象有三个公共点时,求k的值;(3)、如图2,如果把直线沿y轴向上平移至经过点 , 与抛物线的交点分别是 , , 直线交于点 , 过点作于点 , 若 . 求点的坐标.29. 阅读下面方框内的内容,并完成相应的任务.
(1)、求抛物线的解析式;(2)、如图1,如果把抛物线x轴下方的部分沿x轴翻折 , 抛物线的其余部分保持不变,得到一个新图象.当平面内的直线与新图象有三个公共点时,求k的值;(3)、如图2,如果把直线沿y轴向上平移至经过点 , 与抛物线的交点分别是 , , 直线交于点 , 过点作于点 , 若 . 求点的坐标.29. 阅读下面方框内的内容,并完成相应的任务.小丽学习了方程、不等式、函数后提出如下问题:如何求不等式的解集?
通过思考,小丽得到以下3种方法:
方法1:方程的两根为 , , 可得函数的图象与x轴的两个交点横坐标为、 , 画出函数图象,观察该图象在x轴下方的点,其横坐标的范围是不等式的解集.
方法2:不等式可变形为 , 问题转化为研究函数与的图象关系.画出函数图象,观察发现:两图象的交点横坐标也是、3;的图象在的图象下方的点,其横坐标的范围是该不等式的解集.
方法3:当时,不等式一定成立;当时,不等式变为;当时,不等式变为 . 问题转化为研究函数与的图象关系…
任务:
(1)、不等式的解集为;(2)、3种方法都运用了____数学思想方法(从下面选项中选1个序号即可);A、分类讨论 B、转化思想 C、特殊到一般 D、数形结合30. 端午节前夕,某批发部购入一批进价为8元/袋的粽子,销售过程中发现:日销量y(袋)与售价x(元/袋)满足如图所示的一次函数关系. (1)、求y与x之间的函数关系式;(2)、每袋粽子的售价定为多少元时,所获日销售利润最大,最大日销售利润是多少元?31. 如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)、求y与x之间的函数关系式;(2)、每袋粽子的售价定为多少元时,所获日销售利润最大,最大日销售利润是多少元?31. 如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化. (1)、在这个变化过程中,自变量、因变量各是什么?(2)、若小正方形的边长为 , 图中阴影部分的面积为 , 请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.32. 某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.(1)、求两种商品的销售单价.(2)、经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?33. 一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为 .
(1)、在这个变化过程中,自变量、因变量各是什么?(2)、若小正方形的边长为 , 图中阴影部分的面积为 , 请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.32. 某商场销售两种商品,每件进价均为20元.调查发现,如果售出种20件,种10件,销售总额为840元;如果售出种10件,种15件,销售总额为660元.(1)、求两种商品的销售单价.(2)、经市场调研,种商品按原售价销售,可售出40件,原售价每降价1元,销售量可增加10件;种商品的售价不变,种商品售价不低于种商品售价.设种商品降价元,如果两种商品销售量相同,求取何值时,商场销售两种商品可获得总利润最大?最大利润是多少?33. 一名运动员在高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面的高度与离起跳点A的水平距离之间的函数关系如图所示,运动员离起跳点A的水平距离为时达到最高点,当运动员离起跳点A的水平距离为时离水面的距离为 . (1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.34. 如图,抛物线与x轴交于点A和点 , 与y轴交于点 , 点P为第一象限内抛物线上的动点过点P作轴于点E,交于点F.
(1)、求y关于x的函数表达式;(2)、求运动员从起跳点到入水点的水平距离的长.34. 如图,抛物线与x轴交于点A和点 , 与y轴交于点 , 点P为第一象限内抛物线上的动点过点P作轴于点E,交于点F. (1)、求抛物线的解析式;(2)、如图1,当的周长是线段长度的2倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线顶点时,点Q是y轴上的动点,连接 , 过点B作直线 , 连接并延长交直线于点M.当时,请直接写出点Q的坐标.35. 在平面直角坐标系中,抛物线经过点和 , 其顶点的横坐标为 .
(1)、求抛物线的解析式;(2)、如图1,当的周长是线段长度的2倍时,求点P的坐标;(3)、如图2,当点P运动到抛物线顶点时,点Q是y轴上的动点,连接 , 过点B作直线 , 连接并延长交直线于点M.当时,请直接写出点Q的坐标.35. 在平面直角坐标系中,抛物线经过点和 , 其顶点的横坐标为 . (1)、求抛物线的表达式.(2)、若直线与轴交于点 , 在第一象限内与抛物线交于点 , 当取何值时,使得有最大值,并求出最大值.(3)、若点为抛物线的对称轴上一动点,将抛物线向左平移个单位长度后,为平移后抛物线上一动点在的条件下求得的点 , 是否能与、、构成平行四边形?若能构成,求出点坐标;若不能构成,请说明理由.36. 抛物线与轴交于点 , 与直线交于点、点 .
(1)、求抛物线的表达式.(2)、若直线与轴交于点 , 在第一象限内与抛物线交于点 , 当取何值时,使得有最大值,并求出最大值.(3)、若点为抛物线的对称轴上一动点,将抛物线向左平移个单位长度后,为平移后抛物线上一动点在的条件下求得的点 , 是否能与、、构成平行四边形?若能构成,求出点坐标;若不能构成,请说明理由.36. 抛物线与轴交于点 , 与直线交于点、点 . (1)、求抛物线的解析式;(2)、若抛物线与轴交于点、点 , 连接 , 是线段上的任意一点,当为等腰三角形时,请你直接写出点的坐标;(3)、若点是直线的下方该抛物线上的一点不与点、点重合 , 使得的面积最大,请你求出点的坐标,并求出的面积最大值;(4)、如图,线段在线段上移动点与点不重合,点与点不重合 , 且 , 若点的横坐标为 , 过点作轴的垂线与轴交于点 , 过点作轴的垂线与抛物线交于点以点、、、为顶点的四边形能否为平行四边形?若能,请你直接写出的值;若不能,请说明理由.
(1)、求抛物线的解析式;(2)、若抛物线与轴交于点、点 , 连接 , 是线段上的任意一点,当为等腰三角形时,请你直接写出点的坐标;(3)、若点是直线的下方该抛物线上的一点不与点、点重合 , 使得的面积最大,请你求出点的坐标,并求出的面积最大值;(4)、如图,线段在线段上移动点与点不重合,点与点不重合 , 且 , 若点的横坐标为 , 过点作轴的垂线与轴交于点 , 过点作轴的垂线与抛物线交于点以点、、、为顶点的四边形能否为平行四边形?若能,请你直接写出的值;若不能,请说明理由.
-