中考数学第一轮复习:反比例函数
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 下列式子中,y是 的反比例函数的是 ( )A、 B、 C、 D、2. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为 , 设土石方日平均运送量为V(单位:/天),完成运送任务所需要的时间为t(单位:天),则V与t满足( )A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系3. 函数与在同一平面直角坐标系中的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,正比例函数与反比例函数的图象交于、两点,当时,的取值范围是( )
4. 如图,正比例函数与反比例函数的图象交于、两点,当时,的取值范围是( ) A、或 B、或 C、或 D、或5. 如图,A、B是函数的图像上关于原点对称的任意两点,轴,轴,的面积记为S,则( )
A、或 B、或 C、或 D、或5. 如图,A、B是函数的图像上关于原点对称的任意两点,轴,轴,的面积记为S,则( ) A、 B、 C、 D、6. 若点、、在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、7. 如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A、 B、 C、 D、6. 若点、、在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、7. 如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( ) A、3 B、-6 C、6 D、-38. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A、3 B、-6 C、6 D、-38. 某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )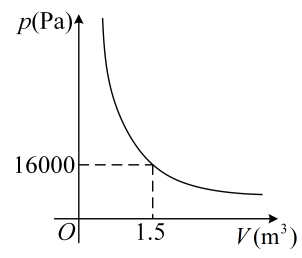 A、不小于 B、不大于 C、不小于 D、不大于9. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、不小于 B、不大于 C、不小于 D、不大于9. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、410. 如图,在平面直角坐标系中,的边在x轴正半轴上,其中 , , 点C为斜边的中点,反比例函数的图象过点C且交线段于点D,连接 , , 若 , 则的值为( )
A、1 B、 C、2 D、410. 如图,在平面直角坐标系中,的边在x轴正半轴上,其中 , , 点C为斜边的中点,反比例函数的图象过点C且交线段于点D,连接 , , 若 , 则的值为( ) A、 B、 C、 D、311. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、 B、 C、 D、311. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )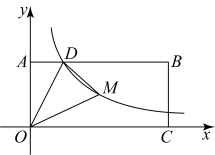 A、2 B、3 C、4 D、512. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板人的质量m之间的函数关系式为 , 其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( )
A、2 B、3 C、4 D、512. 一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻 , 与踏板人的质量m之间的函数关系式为 , 其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( ) A、用含I的代数式表示为 B、电子体重秤可称的最大质量为120千克 C、当时,若电源电压U为12(伏),则定值电阻最小为70(欧) D、当时,若定值电阻为40(欧),则电源电压U最大为10(伏)
A、用含I的代数式表示为 B、电子体重秤可称的最大质量为120千克 C、当时,若电源电压U为12(伏),则定值电阻最小为70(欧) D、当时,若定值电阻为40(欧),则电源电压U最大为10(伏)二、填空题
-
13. 在函数中,自变量的取值范围是.14. 看一本120页的书,平均每天看的页数和看完全书所需的天数之间的关系式为 , 和成比例.15. 已知反比例函数的图象经过点 , 则a的值为 .16. 如图是反比例函数的图象,则的值可能是.(写出一个可能的值即可).
 17. 如图,已知的顶点分别在反比例函数和的图象上,且轴.若的面积为3,则 .
17. 如图,已知的顶点分别在反比例函数和的图象上,且轴.若的面积为3,则 . 18. 如图,在平面直角坐标系中,点的坐标为 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 点恰好落在反比例函数()的图象上,则的值是 .
18. 如图,在平面直角坐标系中,点的坐标为 , 将线段绕点逆时针旋转 , 得到线段 , 连接 , 点恰好落在反比例函数()的图象上,则的值是 .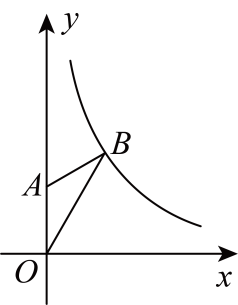 19. 正比例函数的图象与反比例函数的图象相交于A , B两点,过点A作轴,垂足为点C , 连接 , 则的面积是 .20. 如图,在矩形中, , F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= .
19. 正比例函数的图象与反比例函数的图象相交于A , B两点,过点A作轴,垂足为点C , 连接 , 则的面积是 .20. 如图,在矩形中, , F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= . 21. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则.
21. 如图,矩形的顶点在反比例函数的图像上,顶点在第一象限,对角线轴,交轴于点.若矩形的面积是 , 则. 22. 如图,在平面直角坐标系中,反比例函数是常数)在第一象限部分的图象与矩形OABC的两边AB和BC分别交于D,F两点,将沿OD翻折得到的延长线恰好经过点.若 , 则的值是.
22. 如图,在平面直角坐标系中,反比例函数是常数)在第一象限部分的图象与矩形OABC的两边AB和BC分别交于D,F两点,将沿OD翻折得到的延长线恰好经过点.若 , 则的值是.
三、计算题
-
23. 如图,在正方形ABCD中,点A的坐标为( , ),点D的坐标为( , ),且AB∥y轴,AD∥x轴. 点P是抛物线 上一点,过点P作PE⊥x轴于点E , PF⊥y轴于点 F .
 (1)、直接写出点 的坐标;(2)、若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;(3)、以点E为顶点的抛物线 经过点F , 当点P在正方形ABCD内部(不包含边)时,求a的取值范围.24. 如图,抛物线L: (常数t>0)与x轴从左到右的交点为B , A , 过线段OA的中点M作MP⊥x轴,交双曲线 于点P , 且OA·MP=12.
(1)、直接写出点 的坐标;(2)、若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;(3)、以点E为顶点的抛物线 经过点F , 当点P在正方形ABCD内部(不包含边)时,求a的取值范围.24. 如图,抛物线L: (常数t>0)与x轴从左到右的交点为B , A , 过线段OA的中点M作MP⊥x轴,交双曲线 于点P , 且OA·MP=12.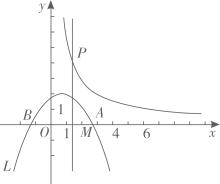 (1)、求k值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G , 用t表示图象G最高点的坐标;(4)、设L与双曲线有个交点的横坐标为x0 , 且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
(1)、求k值;(2)、当t=1时,求AB长,并求直线MP与L对称轴之间的距离;(3)、把L在直线MP左侧部分的图象(含与直线MP的交点)记为G , 用t表示图象G最高点的坐标;(4)、设L与双曲线有个交点的横坐标为x0 , 且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.四、解答题
-
25. 如图,一次函数与反比例函数的图象交于、两点,与轴交于点.
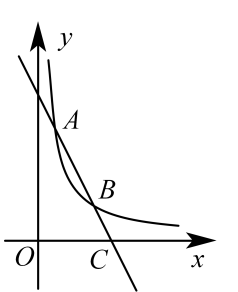 (1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.26. 如图,直线与双曲线相交于点 , 轴于点 , 以为边在右侧作正方形 , 与双曲线相交于点 , 连结、 .
(1)、求一次函数与反比例函数的解析式;(2)、若点在轴上,且的面积为 , 求点的坐标.26. 如图,直线与双曲线相交于点 , 轴于点 , 以为边在右侧作正方形 , 与双曲线相交于点 , 连结、 .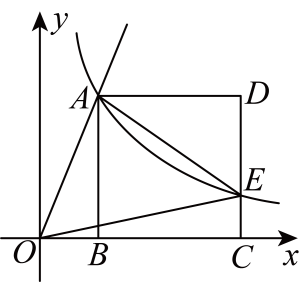 (1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.27. 实验数据显示,一般情况下,成人喝低度白酒后,小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;小时后(包括小时)y与x成反比例.根据图中提供的信息,解答下列问题:
(1)、当时,求点的坐标;(2)、当时,求的值;(3)、是否存在实数 , 满足 , 若存在,求出的值;若不存在,请说明理由.27. 实验数据显示,一般情况下,成人喝低度白酒后,小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;小时后(包括小时)y与x成反比例.根据图中提供的信息,解答下列问题: (1)、写出一般情况下,成人喝低度白酒后,y与x之间的函数关系式及相应的自变量取值范围.(2)、按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
(1)、写出一般情况下,成人喝低度白酒后,y与x之间的函数关系式及相应的自变量取值范围.(2)、按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完低度白酒,第二天早上7:00能否驾车去上班?请说明理由.五、实践探究题
-
28. 类比一次函数和反比例函数的学习经验,某数学实验小组尝试探究“的函数图象与性质”,进行了如下活动.(1)、【小组合作 讨论交流】
同学甲说:“我们可以从表达式分析,猜想图像位置.”
同学乙回应道:“是的,因为自变量x的取值范围是 , 所以图像与y轴不相交.”
同学丙补充说:“又因为函数值y大于0,所以图像一定在第象限.”
……
(2)、【独立操作 探究性质】在平面直角坐标系中,画出的图像.

结合图像,描述函数图象与性质:
①函数的图像是两条曲线;
②该函数图象关于 ▲ 对称;
③图像的增减性是 ▲ ;
④同学丁说:“将第二象限的曲线绕原点顺时针旋转后,与第一象限的曲线重合.”请你判断同学丁的说法是否正确?若错误,举出反例;若正确,请说明理由.
(3)、【拓展探究 综合应用】直接写出不等式的解集是.
29. 阅读理解题:阅读材料:
如图1,四边形是矩形,是等腰直角三角形,记为、为 , 若 , 则 .

证明:设 , ∵ , ∴ ,
易证
∴ ,
∴
∴ ,
若时,当 , 则 .
同理:若时,当 , 则 .
根据上述材料,完成下列问题:
如图2,直线与反比例函数的图象交于点 , 与轴交于点 . 将直线绕点顺时针旋转后的直线与轴交于点 , 过点作轴于点 , 过点作轴于点 , 已知 .
 (1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.30. 【定义】在平面直角坐标系xOy中,对于点和点 , 给出如下定义:若 , 则称点Q为点P的限变点,例如:点的限变点的坐标是 , 点的限变点的坐标是 .
(1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.30. 【定义】在平面直角坐标系xOy中,对于点和点 , 给出如下定义:若 , 则称点Q为点P的限变点,例如:点的限变点的坐标是 , 点的限变点的坐标是 .【应用】
(1)、①点的限变点的坐标是;②以下三个选项中的点是反比例函数图象上某一个点的限变点的是()
A. B. C.
(2)、若点P在一次函数的图象上,请在下图平面直角坐标系中,画出点P的限变点Q的函数图象,并根据图象直接写出点Q的纵坐标的取值范围为 . (3)、【拓展】
(3)、【拓展】我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休”.若点P在关于x的二次函数的图象上,其限变点Q的纵坐标的取值范围是或 , 其中 , 令 , 求s关于t的函数解析式.
六、综合题
-
31. 如图,点A在反比例函数的图象上,点C是点A关于y轴的对称点,的面积是8.
 (1)、求反比例函数的解析式;(2)、当点A的横坐标为2时,过点C的直线与反比例函数的图象相交于点P,求交点P的坐标.32. 如图,在平面直角坐标系中,四边形是边长为的正方形.点 , 在坐标轴上.反比例函数的图象经过点 .
(1)、求反比例函数的解析式;(2)、当点A的横坐标为2时,过点C的直线与反比例函数的图象相交于点P,求交点P的坐标.32. 如图,在平面直角坐标系中,四边形是边长为的正方形.点 , 在坐标轴上.反比例函数的图象经过点 . (1)、求反比例函数的表达式;(2)、点D在反比例函数图象上,且横坐标大于2, . 求直线的函数表达式.33. 一次函数与反比例函数的图象交于 , 两点,点的坐标为 .
(1)、求反比例函数的表达式;(2)、点D在反比例函数图象上,且横坐标大于2, . 求直线的函数表达式.33. 一次函数与反比例函数的图象交于 , 两点,点的坐标为 . (1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.34. 在学习反比例函数后,小华在同一个平面直角坐标系中画出了和的图像,两个函数图象交于两点,在线段上选取一点P,过点P作y轴的平行线交反比例函数图象于点Q(如图1),在点P移动的过程中,发现的长度随着点P的运动而变化.为了进一步研究的长度与点P的横坐标之间的关系,小华提出了下列问题:
(1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.34. 在学习反比例函数后,小华在同一个平面直角坐标系中画出了和的图像,两个函数图象交于两点,在线段上选取一点P,过点P作y轴的平行线交反比例函数图象于点Q(如图1),在点P移动的过程中,发现的长度随着点P的运动而变化.为了进一步研究的长度与点P的横坐标之间的关系,小华提出了下列问题: (1)、设点P的横坐标为x,的长度为y,则y与x之间的函数关系式为;(2)、为了进一步研究(1)中的函数关系,决定运用列表,描点,连线的方法绘制函数的图象:
(1)、设点P的横坐标为x,的长度为y,则y与x之间的函数关系式为;(2)、为了进一步研究(1)中的函数关系,决定运用列表,描点,连线的方法绘制函数的图象:①列表:
x
1
2
3
4
6
9
y
0
m
4
n
0
表中m= ▲ , n= ▲ ;
②描点:根据上表中的数据,在图2中描出各点;
③连线:请在图2中画出该函数的图象.观察函数图象,当 ▲ 时,y的最大值为 ▲ .
(3)、①已知某矩形的一组邻边长分别为m,n,且该矩形的周长W与n存在函数关系 , 求m取最大值时矩形的对角线长.②如图3,在平面直角坐标系中,直线与坐标轴分别交于点A、B,点M为反比例函数上的任意一点,过点M作轴于点C,轴于点D.求四边形面积的最小值.
35. 给某气球充满一定质量的气体,在温度不变时,气球内气体的气压是气体体积()的反比例函数,其图象如图所示.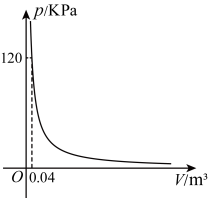 (1)、当气球内的气压超过时,气球会爆炸.若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 , 取3);(2)、请你利用与的关系试解释为什么超载的车辆容易爆胎.36. 如图1,在平面直角坐标系中,点 , 点 , 直线与反比例函数的图象在第一象限交于点 .
(1)、当气球内的气压超过时,气球会爆炸.若将气球近似看成一个球体,试估计气球的半径至少为多少时气球不会爆炸(球体的体积公式 , 取3);(2)、请你利用与的关系试解释为什么超载的车辆容易爆胎.36. 如图1,在平面直角坐标系中,点 , 点 , 直线与反比例函数的图象在第一象限交于点 . (1)、求反比例函数的解析式(2)、如图2,点是反比例函数图象上一点,连接 , 。试问在轴上是否存在一点 , 使△ACD的面积与△ACE的面积相等,若存在,请求出点的坐标;若不存在,请说明理由。(3)、在(2)的条件下,坐标原点O关于点的对称点为 , 且点在轴的正半轴上,若点是反比例函数的第一象限图象上一个动点,连接MG,以MG为边作正方形 , 当顶点恰好落在直线上时,求点M的坐标。
(1)、求反比例函数的解析式(2)、如图2,点是反比例函数图象上一点,连接 , 。试问在轴上是否存在一点 , 使△ACD的面积与△ACE的面积相等,若存在,请求出点的坐标;若不存在,请说明理由。(3)、在(2)的条件下,坐标原点O关于点的对称点为 , 且点在轴的正半轴上,若点是反比例函数的第一象限图象上一个动点,连接MG,以MG为边作正方形 , 当顶点恰好落在直线上时,求点M的坐标。