中考数学第一轮复习：无理方程

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列方程中，属于无理方程的是（）

A、 $x^{2} - \sqrt{2} = 0$ B、 $\sqrt{2 x} = 1$ C、 $\frac{\sqrt{2}}{x} = 1$ D、 $\sqrt{2} x = 0$

查看试题解析
2. 在下列方程中，有实数根的方程的个数有（）
① $\sqrt{x + 2} + 3 = 0$ ；
② $\sqrt{x - 4} + \sqrt{3 - x} = 0$ ；
③ $\sqrt{x + 1} = - x$ ；
④ $\sqrt{2 x - 3} + \sqrt{3 - 2 x} = 0$ ；
⑤ $x^{2} - 2 x + 4 = 0$ ；
⑥ $\frac{2}{x + 1} + \frac{3}{x - 1} = \frac{6}{x^{2} - 1}$ ．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 下列方程中，有实数根的是（　　）

A、 $x^{4} + 2 = 0$ B、 $\sqrt{x - 2} + 1 = 0$ C、 $\sqrt{x - 1} + \sqrt{1 - x} = 0$ D、 $\frac{x}{x^{2} - 1} = \frac{1}{x^{2} - 1}$

查看试题解析
4. 如果关于x的方程 $\sqrt{2 x - 1} + 3 = m$ 没有实数根，那么m的取值范围是（　　）

A、 $m \geq 0$ B、 $m \geq 3$ C、 $m < 0$ D、 $m < 3$

查看试题解析
5. 已知实数a满足 $| 2000 - a | + \sqrt{a - 2001} = a$ ，那么 $a - 2000^{2}$ 的值是（）

A、1999 B、2000 C、2001 D、2002

查看试题解析
6. 下列关于x的方程中，一定有实数根的是（）

A、 $\sqrt{x + 1} + 1 = 0$ B、 $\sqrt{x - 3} = 2 - x$ C、 $\sqrt{x + 1} = 0$ D、 $\sqrt{x + 2} + \sqrt{2 - x} = - 1$

查看试题解析
7. 下列方程，有实数解的是（）

A、 $\sqrt{x - 2} + 1 = 0$ B、 $\frac{x}{x - 2} = \frac{2}{x - 2}$ C、 ${(x + 2)}^{4} - 1 = 0$ D、 $\sqrt{x - 4} + \sqrt{x - 3} = 0$

查看试题解析
8. 下列方程中，有实数解的是（）

A、 $\sqrt{2 x + 1} + 1 = 0$ ； B、 $x^{2} + 3 x + 4 = 0$ ； C、 $2 x^{4} - 1 = 0$ ； D、 $\frac{2}{x - 2} = \frac{x}{x - 2}$ ．

查看试题解析
9. 下列方程中，有实数根的方程是（）

A、 $\sqrt{x} + 1 = 0$ B、 $x^{2} + 1 = 0$ C、 $\sqrt{x} = x$ D、 $x^{2} - x + 1 = 0$

查看试题解析
10. 下列方程中，有一个根是x=2的方程是（）

A、 $\frac{x}{x - 2} = \frac{2}{x - 2}$ B、 $\frac{x - 2}{2} + \frac{2 - x}{x} = 0$ C、 $\sqrt{x - 2} \cdot \sqrt{x - 3} = 0$ D、 $\sqrt{x - 6} = 2$

查看试题解析
11. 如果关于 $x$ 的方程 $\sqrt{2 x + m} = x$ 有实数根 $x = 1$ ，那么m的值是（）

A、 $- 1$ B、 $\frac{1}{3}$ C、 $0$ D、 $2$

查看试题解析
12. 下列方程中有实数解的方程是（）

A、 $\frac{2}{x - 2} = \frac{x}{x - 2}$ ； B、 $\sqrt{3 - x} + \sqrt{x - 5} = 2$ ； C、 $x^{3} + 1 = 0$ ； D、 $x^{2} + x + 1 = 0$ ．

查看试题解析
13. 下列方程中，有实数解的是（）

A、 $x^{2} + 1 = 0$ B、 $x + \frac{1}{x} = 1$ C、 $\sqrt{2 x + 3} = - x$ D、 $\frac{x + 2}{x^{2} + 2 x} = 0$

查看试题解析

二、填空题

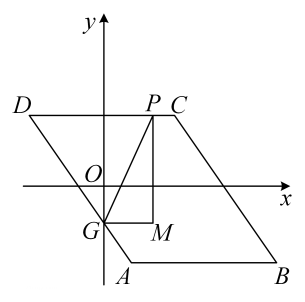
14. 如图， $▱ A B C D$ 中， $A B$ // $x$ 轴， $A B = 12$ ．点A的坐标为 $(2 ， - 8)$ ，点D的坐标为 $(- 6 ， 8)$ ，点B在第四象限，点G是AD与y轴的交点，点P是CD边上不与点C，D重合的一个动点，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，点P的坐标为．

查看试题解析
15. 如果关于 $x$ 的无理方程 $\sqrt{2 x + m} = x$ 有实数根 $x = 1$ ，那么 $m$ 的值为．

查看试题解析
16. 方程 $\sqrt{x + 1} = 2$ 的根是．

查看试题解析
17. 方程 $(x + 1) \sqrt{x - 1} = 0$ 的根是．

查看试题解析
18. 方程 $\sqrt{2 x + 3} = - x$ 的解为．

查看试题解析
19. 已知关于 $x$ 的方程 $\sqrt{x - 14} = 2$ ，则 $x =$

查看试题解析
20. 方程 $\sqrt{x + 7}$ - x=1的根是．

查看试题解析
21. 方程 $\sqrt{x + 2} = x$ 的根是．

查看试题解析
22. 已知 $| 2022 - a | + \sqrt{a - 2023} = a$ ，则 $a - 2022^{2} =$ .

查看试题解析
23. 方程 $\sqrt{x + 6} = 3$ 的解是．

查看试题解析
24. 方程 $\sqrt{2 x - 5} ＝$ 1的解是．

查看试题解析

三、计算题

25. $\sqrt{2 x + 1} + \sqrt{x} = 1$

查看试题解析
26. 解方程： $\sqrt{2 x - 3} + x = 3$

查看试题解析
27. 解方程： $\sqrt{x + 1} - 1 = x$ ．

查看试题解析

四、解答题

28. 解方程： $y - \sqrt{3 - y} = 1$

查看试题解析
29. 小颖利用平方差公式，自己探究出一种解某一类根式方程的方法.下面是她解方程 $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ＝5的过程.
解：设 $\sqrt{x - 2}$ ﹣ $\sqrt{x - 7}$ ＝m，与原方程相乘得：

（ $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ）×（ $\sqrt{x - 2} - \sqrt{x - 7}$ ）＝5m，

x﹣2﹣（x﹣7）＝5m，解之得m＝1，

∴ $\sqrt{x - 2}$ ﹣ $\sqrt{x - 7}$ ＝1，与原方程相加得：

（ $\sqrt{x - 2}$ ＋ $\sqrt{x - 7}$ ）+（ $\sqrt{x - 2} - \sqrt{x - 7}$ ）＝5＋1，

2 $\sqrt{x - 2}$ ＝6，解之得，x＝11，经检验，x＝11是原方程的根.

学习借鉴解法，解方程 $\sqrt{x - 3}$ ﹣ $\sqrt{x - 6}$ ＝1.

查看试题解析
30. 解方程 $\sqrt{3 x - 2} + \sqrt{x + 3} = 3$

查看试题解析

五、综合题

31.

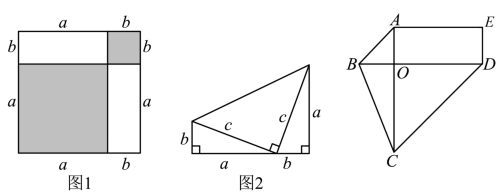(1)、用不同的方法计算图1中阴影部分的面积得到的等式：

(2)、图2是由两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成，试用不同的方法计算这个图形的面积，你能发现什么？说明理由；

(3)、根据上面两个结论，解决下面问题：
① 在直角 $△ A B C$ 中， $∠ C = 90 °$ ，三边分别为a、b、c， $a + b = 7$ ， $a b = 12$ ，求c的值：

② 如图3，五边形ABCDE中，线段AC⊥BD，AC=BD=2，四边形ODEA为长方形，在直角△BOC中，OB=x，OC=y，其周长为n，当n为何值时，长方形AODE的面积为定值，并说明理由.

查看试题解析
32. 类比和转化是数学中解决新的问题时最常用的数学思想方法.
【回顾旧知，类比求解】

解方程： $\sqrt{x + 1} = 2$ .

解：去根号，两边同时平方得一元一次方程 ▲ ，解这个方程，得 $x =$ ▲ .

经检验， $x =$ ▲ 是原方程的解.

(1)、 $\sqrt{x - 2} - 3 = 0$ ；

(2)、 $\sqrt{4 x^{2} + 5 x} - 2 x = 1$ .

查看试题解析
33.

(1)、方程|4x-8|+ $\sqrt{x - y - m}$ =0，当y>0 时，m的取值范围是（）

A、0<m<1 B、m≥2 C、m<2 D、m≤2

(2)、方程(x- 3) $\sqrt{2 - x}$ =0的解是

查看试题解析

六、实践探究题

34. 阅读材料，并回答问题：
小亮在学习分式过程中，发现可以运用“类比”的方法，达成事半功倍的学习效果，比如学习异分母分式加减可以类比异分母分数的加减，先通分，转化为同分母分式加减进行运算，解分式方程可以类比有分母的一元一次方程，先去分母，转化为整式方程求解；比较分式的大小，可以类比整式比较大小运用的“比差法”……

问题：

(1)、材料中分式“通分”的依据是；“将分式方程转化为整式方程”的“去分母”的依据是；

(2)、类比解分式方程的思想方法，解方程： $\sqrt{1 - 2 x} = 3$ ；

(3)、数学家斐波那契编写的《算经》中有如下问题：甲、乙两组人各自平分钱，已知两组人数相同，相关信息如表：

组别

人数（人）

总金额（元）

甲

$b^{2}$

乙

$2 b - 5$

试比较甲乙两组哪组人均分的钱多？

查看试题解析
35. 阅读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式.求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组.求解一元二次方程，把它转化为两个一元一次方程来解.求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验.各类方程的解法不尽相同，但是它们有一个共同的基本数学思想 $- -$ 转化，把未知转化为已知.

用“转化”的数学思想，我们还可以解一些新的方程.例如，一元三次方程x³+x²-2x=0，可以通过因式分解把它转化为x(x²+x-2)=0，解方程x=0和x²+x-2=0，可得方程x³+x²-2x=0的解.

(1)、问题：方程x³+x²-2x=0的解是x₁=0，x₂= ， x₃=；

(2)、拓展：用“转化”思想求方程 $\sqrt{2 x + 3} = x$ 的解；

(3)、应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C.求AP的长.

查看试题解析

组别	人数（人）	总金额（元）
甲		$b^{2}$
乙		$2 b - 5$