中考数学第一轮复习：一元二次方程

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列方程中，一定为一元二次方程的是（　　）

A、 $x + 3 y = 4$ B、 $5 y = 5 y^{2}$ C、 $4 x - 4 = 0$ D、 $a x^{2} - x = 1$

查看试题解析
2. 某车间有26名工人，每人每天能生产螺栓12个或螺母18个. 若要使每天生产的螺栓和螺母按1：2配套，则分配几人生产螺栓？设分配x名工人生产螺栓，其他工人生产螺母，所列方程正确的是（　）

A、12x=18（26-x） B、18x=12（26-x） C、2×18x=12（26-x） D、2×12x=18（26-x）

查看试题解析
3. 下列方程中，有实数根的方程是（）

A、 $\sqrt{x + 1} = - 1$ B、 $x^{3} + 2 = 0$ C、 $\frac{x}{x^{2} - 1} = \frac{1}{x^{2} - 1}$ D、 $x^{2} - 2 x + 3 = 0$

查看试题解析

4. 根据下列表格对应值：

$x$	$3.24$	$3.25$	$3.26$
$a x^{2} + b x + c$	$- 0.02$	$0.01$	$0.03$

判断关于 $x$ 的方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的一个解 $x$ 的范围是（）

A、

x < 3.24

B、

3.24 < x < 3.25

C、

3.25 < x < 3.26

D、

3.25 < x < 3.28

查看试题解析

5. 利用公式法求解可得一元二次方程式 $3 x^{2} - 11 x - 1 = 0$ 的两解为 $a$ 、 $b$ ，且 $a > b$ ，求a值为何（）

A、 $\frac{- 11 + \sqrt{109}}{6}$ B、 $\frac{- 11 + \sqrt{133}}{6}$ C、 $\frac{11 + \sqrt{109}}{6}$ D、 $\frac{11 + \sqrt{133}}{6}$

查看试题解析
6. 若方程 $3 x^{2} - 10 x + m = 0$ 有两个同号不等的实数根，则 $m$ 的取值范围是（）

A、 $m \geq 0$ B、 $m > 0$ C、 $0 < m < \frac{25}{3}$ D、 $0 < m \leq \frac{25}{3}$

查看试题解析
7. 某商店将进货价格为20元的商品按单价36元售出时，能卖出200个．已知该商品单价每上涨1元，其销售量就减少5个．设这种商品的售价上涨 $x$ 元时，获得的利润为1200元，则下列关系式正确的是（　　）

A、 $(x + 16) (200 - 5 x) = 1200$ B、 $(x + 16) (200 + 5 x) = 1200$ C、 $(x - 16) (200 + 5 x) = 1200$ D、 $(x - 16) (200 - 5 x) = 1200$

查看试题解析
8. 一次聚会，每个参加聚会的人互送一件不同的小礼物，有人统计一共送了 $56$ 件小礼物，如果参加这次聚会的人数为 $x$ ，根据题意可列方程为（）

A、 $x (x + 1) = 56$ B、 $x (x - 1) = 56$ C、 $2 x (x + 1) = 56$ D、 $x (x - 1) = 56 \times 2$

查看试题解析
9. 要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A、 $\frac{1}{2} x (x + 1) = 4 \times 7$ B、 $\frac{1}{2} x (x - 1) = 4 \times 7$ C、 $x (x + 1) = 28$ D、 $x (x - 1) = 28$

查看试题解析
10. 如果关于x的一元二次方程 $x^{2} + 2 (m - 1) x + 16 = 0$ 有两个相等的实数根，那么m的值可为（）

A、5 B、 $- 3$ C、 $- 5$ 或3 D、5或 $- 3$

查看试题解析

二、填空题

11. 方程 ${(x - 1)}^{2} = 27$ 的根是．

查看试题解析
12. 方程 $\sqrt{x - 1} = 1 - x$ 的解为．

查看试题解析
13. 若 $m = \sqrt{2023} + 2$ ，则式子 $m^{2} - 4 m + 5$ 的值为．

查看试题解析
14. 新型冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将会有225人感染，若设1人平均感染x人，则x的值为。

查看试题解析
15. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为15m的住房墙，另外三边用27m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，则所围矩形猪舍的长为宽为时面积为96 $m^{2}$ ．

查看试题解析
16. 有学者认为，阿拉伯数学家花拉子米的《代数学》关于一元二次方程的几何求解法与中国古代数学的“出入相补原理”相近，可能受到中国传统数学思想的影响，花拉子米关于 $x^{2} + 10 x = 39$ 的几何求解方法如图1，在边长为x的正方形的四个边上向外做边长为x和 $\frac{5}{2}$ 的矩形，再把它补充成一个边长为 $x + 5$ 的大正方形，我们得到大正方形的面积为 ${(x + 5)}^{2} = x^{2} + 10 x + 25 = 39 + 25 = 64$ （因为 $x^{2} + 10 x = 39$ ）．所以大正方形边长为 $x + 5 = 8$ ，得到 $x = 3$ ．思考：当我们用这种方法寻找 $x^{2} + 6 x = 7$ 的解时，如图2中间小正方形的边长x为；阴影部分每个正方形的边长为．

查看试题解析
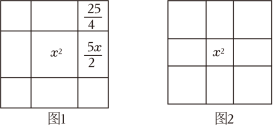17. 已知实数 $a \neq b \neq c$ ，且满足 $\frac{c}{a} = a + 3$ ， $\frac{c}{b} = b + 3$ ．请解决下列问题：

(1)、当 $c = - 1$ 时， $a + b$ 的值为；

(2)、当 $c > 0$ 时， $\frac{a^{2} + b^{2} - 9}{c}$ 的值为．

查看试题解析
18. 有一个正方形的花园，如果它的边长增加 $2 m$ ，那么花园面积将增加 $16 m^{2}$ ，则原花园的面积为．

查看试题解析
19. 定义：若x，y满足 $x^{2} = 4 y + t ， y^{2} = 4 x + t$ 且 $x \neq y$ （t为常数），则称点 $M (x ， y)$ 为“和谐点”．

(1)、若 $P (3 ， m)$ 是“和谐点”，则 $m =$ ．

(2)、若双曲线 $y = \frac{k}{x} (- 3 < x < - 1)$ 存在“和谐点”，则k的取值范围为．

查看试题解析
20. 若 $W = 5 x^{2} - 4 x y + y^{2} - 2 y + 8 x + 3$ （ $x 、 y$ 为实数），则 $W$ 的最小值为.

查看试题解析

三、计算题

21. 用适当方法解方程：

(1)、 $y^{2} - 15 = 2 y$ ；

(2)、x2+23x+3=0；

(3)、 ${(x - 2)}^{2} + {(x + 2)}^{2} = 4 x - 6$ ；

(4)、 $4 (x + 2) (x - 3) = {(x - 3)}^{2}$ ．

查看试题解析
22. 解关于y的方程：by²﹣1＝y²+2．

查看试题解析
23. 已知关于x的方程 $x^{2} + 2 (a - 1) x + a^{2} - 7 a - 4 = 0$ 的两根为 $x_{1} ， x_{2}$ ，且满足 $x_{1} x_{2} - 3 x_{1} - 3 x_{2} - 2 = 0$ ，求 $(1 + \frac{4}{a^{2} - 4}) \frac{a + 2}{a}$ 的值．

查看试题解析

四、解答题

24. 已知关于 $x$ 的一元二次方程 $x^{2} - (2 k - 1) x + k^{2} = 0$ 有两个不相等的实数根

(1)、求 $k$ 的取值范围；

(2)、若此方程的两实数根 $x_{1} . x_{2}$ 满足 $(x_{1} - 1) (x_{2} - 1) = 5$ ，求 $k$ 的值

查看试题解析
25. 已知关于x的一元二次方程 $x^{2} - (2 m + 1) x + m^{2} + m = 0$ ．

(1)、求证：无论m取何值，方程都有两个不相等的实数根；

(2)、如果方程的两个实数根为 $x_{1}$ ， $x_{2} (x_{1} > x_{2})$ ，且 $\frac{x_{2} + 3}{x_{1}}$ 为整数，求整数m所有可能的值．

查看试题解析
26. 已知关于x的一元二次方程 $x^{2} - (2 k + 1) x + k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1}$ 、 $x_{2}$ ．

(1)、求k的取值范围；

(2)、若（填序号），求k的值．（从①x₁•x₂＝2；②x₁+x₂＝3；③x₁-x₂＝1中选择一个作为条件，补充完整题目，并完成解答．）

查看试题解析
27. 台风“杜苏芮”牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动，第一天收到捐款3000元，第三天收到捐款4320元．

(1)、如果第二天、第三天收到捐款的增长率相同，求捐款增长率；

(2)、按照（1）中收到的捐款的增长速度，第四天该单位能收到多少捐款？

查看试题解析
28. 如图，有一块长为30米，宽为20米的矩形场地，计划在该场地上修建两条互相垂直的小道，横向小道与坚向小道的宽比为 $2 ： 3$ ，余下矩形场地建成草坪，草坪的面积为486平方米，请求出横向小道的宽．

查看试题解析
29. 在 $△ A B C$ 中， $∠ A C B = 90 ° ， A C = 16 c m ， B C = 12 c m$ ，动点M、N分别从点A和点C同时开始移动，点M的速度为 $2 c m$ /秒，点N的速度为 $3 c m$ /秒，点M移动到点C后停止，点N移动到点B后停止．问经过几秒钟， $△ M C N$ 的面积为 $36 c m^{2}$ ？

查看试题解析

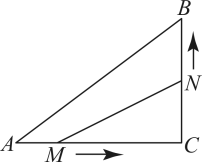
五、综合题

30. 已知，一辆汽车在笔直的公路上刹车后，该车的速度 $v ($ 米 $/$ 秒 $)$ 与时间 $t ($ 秒 $) (0 < t \leq 15)$ 之间满足一次函数关系，其图象如图所示；

(1)、求 $v$ 与 $t$ 之间的函数关系式；

(2)、已知汽车在该运动状态下，一段时间内向前滑行的距离等于这段时间内的平均速度乘以时间 $($ 该运动状态下的平均速度 $v =$ $\frac{v_{1} + v_{2}}{2}$ ， $v_{1}$ 表示这段时间起始时刻的速度， $v_{2}$ 表示这段时间结束时刻的速度 $)$ ．若该车刹车后 $t$ 秒内向前滑行了 $378$ 米，求 $t$ 的值．

查看试题解析
31. 请阅读下列材料：
问题：已知方程 $x^{2} + x - 1 = 0$ ，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为 $y$ ，则 $y = 2 x$ ，所以 $x = \frac{y}{2}$ ，把 $x = \frac{y}{2}$ 代入已知方程，得 ${(\frac{y}{2})}^{2} + \frac{y}{2} - 1 = 0$ ；化简，得 $y^{2} + 2 y - 4 = 0$ ；故所求方程为 $y^{2} + 2 y - 4 = 0$ ．
这种利用方程根的代换求新方程的方法，我们称为“换根法”；
请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：

(1)、已知方程 $x^{2} + 3 x - 2 = 0$ ，求一个一元二次方程，使它的根分别为已知方程根的相反数；

(2)、已知关于 $x$ 的一元二次方程 $a x^{2} - b x + c = 0 (a \neq 0)$ 有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

查看试题解析
32. 若我们规定：在平面直角坐标系中，点 $P$ 的坐标为 $(x ， y_{1})$ ，点 $Q$ 的坐标为 $(x ， y_{2})$ ， $y_{1}$ 和 $y_{2}$ 的差构成一个新函数 $y$ ，即 $y = y_{1} - y_{2}$ ．称 $y$ 是 $y_{1} - y_{2}$ 的“数天数函数”， $P$ 为“天数点 $1$ ”， $Q$ 为“天数点 $2$ ”．（亲爱的同学们：愿你们在“数天数”中不负韶华，一次次交上自己满意的答卷．）

(1)、已知“天数点 $1$ ”为点 $A (x$ ， $k x + 4$ $)$ ， “天数点 $2$ ”为点 $B (x$ ， $2 x)$ ．点 $C (2$ ， $3)$ 在“数天数函数” $y = y_{1} - y_{2}$ 图像上，求 $y$ 的解析式；

(2)、已知“天数点 $1$ ”为点 $M (x$ ， $x^{2} + 3$ $)$ ， “天数点 $2$ ”为点 $N (x$ ， $3 x)$ ， $y$ 是“数天数函数，求 $x + y$ 的最小值．

(3)、关于 $x$ 的方程 $x^{2} + (m - 2) x + \frac{1}{2} m - 3 = 0$ 的两个实数根 $x_{1}$ 、 $x_{2}$ ， “数天数函数” $S = S_{1} - S_{2}$ ．若 $S_{1} = 2 x_{1}$ ， $S_{2} = - x_{2}$ ，且 $S = m + 1$ ，求 $m$ 的值．

查看试题解析

六、实践探究题

33. 先阅读下面的内容，再解答问题．
【阅读】例题：求多项式 $m^{2} + 2 m n + n^{2} + 4$ 的最小值．

解： $m^{2} + 2 m n + n^{2} + 4 = (m^{2} + 2 m n + n^{2}) + 4 = {(m + n)}^{2} + 4$ ，

∵ ${(m + n)}^{2} \geq 0$ ， ∴ ${(m + n)}^{2} + 4 \geq 4$

∴多项式 $m^{2} + 2 m n + n^{2} + 4$ 的最小值是4

(1)、请写出例题解答过程中把一个三项二次式转化为一个二项式的平方运用的公式是；

(2)、求多项式 $- 2 x^{2} + 4 x y - 2 y^{2} + 30$ 的最大值．

查看试题解析

34. 综合实践：

项目主题	“亚运主题”草坪设计
项目情境	为了迎亚会，同学们参与一块长为40米，宽为30米的矩形“亚运主题”草坪方案设计的项目学习．以下为项目学习小组对草坪设计的研究过程．
活动任务一	请设计两条相同宽度的小路连接矩形草坪两组对边．小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一	（1）项目小组设计出来的四种方案小路面积的大小关糸？ ①直观猜想：我认为 ▲ ；（请用简洁的语言或代数式表达你的猜想） ②具体验证：选择最简单的甲、乙方案，假设小路宽为1米，则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ； ③一般验证：若小路宽为x米，则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ ．
活动任务二	为施工方便，学校选择甲种方案设计，并要求除小路后草坪面积约为1064平方米．
驱动问题二	（2）请计算两条小路的宽度是多少？
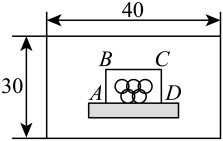
活动任务三	为了布置五环标志等亚运元素，将在草坪上的亚运宣传主题墙前，用篱笆围（三边）成面积为100平方米的矩形 $A B C D$ ，如图．
驱动问题三	（3）为了使篱笆恰好用完同时围住三面，项目小组的同学对下列问题展开探究，其中矩形宽 $A B = x$ ，长 $B C = y$ ． ①若30米长的篱笆，请用两种不同的函数表示y关于x的函数关系． ②数学之星小明提出一个问题：若a米长的篱笆恰好用完，且有两种不同方案可以选择，使得两种方案的宽之和小于15米，甲同学说“篱笆的长可以是28米”，乙同学说“篱笆的长可以是32米”，你认为他们俩的说法对吗？请说明理由．

查看试题解析

35. 阅读材料，解答问题：材料1为了解方程（x²）²－13x²＋36＝0，如果我们把x²看作一个整体，然后设y＝x² ，则原方程可化为y²－13y＋36＝0，经过运算，原方程的解为 $x_{1 ， 2} = \pm 2$ ， $x_{3 ， 4} = \pm 3$ ．我们把以上这种解决问题的方法通常叫做换元法．
材料2已知实数m，n满足m²－m－1＝0，n²－n－1＝0，且m≠n，显然m，n是方程x²－x－1＝0的两个不相等的实数根，由韦达定理可知m＋n＝1，mn＝－1．

根据上述材料，解决以下问题：

(1)、直接应用：解方程：x⁴－x²－6＝0．

(2)、间接应用：已知实数m，n满足：m²－7m＋2＝0，n²－7n＋2＝0，求 $\frac{n}{m} + \frac{m}{n}$ 的值．

(3)、拓展应用：已知实数x，y满足： $\frac{4}{x^{4}} - \frac{2}{x^{2}} = 3 ， y^{4} + y^{2} = 3$ ，求 $\frac{4}{x^{4}} + y^{4}$ 的值．

查看试题解析
36. 材料一：我们定义：如果两个多项式A与B的差为常数，且这个常数为正数，则称A是B的“雅常式”，这个常数称为A关于B的“雅常值”．如多项式 $A = a^{2} + 2 a + 1$ ， $B = (a + 4) (a - 2)$ ， $A - B = (a^{2} + 2 a + 1) - (a + 4) (a - 2) = (a^{2} + 2 a + 1) - (a^{2} + 2 a - 8) = 9$ ，则A是B的“雅常式”，A关于B的“雅常值”为9．
材料二：把形如 $a x^{2} + b x + c$ 的二次三项式配成完全平方式的方法叫做配方法，配方法的基本形式是完全平方公式的逆写，即 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$ ．
例如：我们可以将代数式 $a^{2} + 6 a + 10$ 进行变形，其过程如下：
$a^{2} + 6 a + 10 = (a^{2} + 6 a) + 10 = (a^{2} + 6 a + 9) + 10 - 9 = (a + 3)^{2} + 1$
∵ $(a + 3)^{2} \geq 0$ ， ∴ $(a + 3)^{2} + 1 \geq 1$ ，因此，该式有最小值1．

(1)、已知多项式M是多项式N的“雅常式”，如果 $M = a^{2} + 2 a - 1$ ， $N = (a + 3) (a - 1)$ ，请求出M关于N的“雅常值”；

(2)、多项式 $Q = x^{2} + 2 x - n$ 的最小值为 $- 3$ ，求出n的值；若 $P = (x + m)^{2}$ （m为常数）是Q的“雅常式”，求P关于Q的“雅常值”．

查看试题解析