中考数学第一轮复习：二元一次方程组

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列方程中，是二元一次方程的是（）

A、 $x y = 1$ B、 $y = 3 x - 1$ C、 $x + \frac{1}{y} = 2$ D、 $x^{2} + x - 1 = 0$

查看试题解析
2. 把方程 $x + y = 3$ 改写成用含x的式子表示y的形式，正确的是（）

A、 $y = x + 3$ B、 $y = - x + 3$ C、 $y = x - 3$ D、 $y = - x - 3$

查看试题解析
3. 下列不是二元一次方程组的是（）

A、 ${\begin{array}{l} 3 x + 2 y = 10 \\ 2 x - 3 y = 5 \end{array}$ B、 ${\begin{array}{l} 3 x + 5 y = 1 \\ 2 x - y = 4 \end{array}$ C、 ${\begin{array}{l} x + 5 y = 1 \\ x - 5 y = 2 \end{array}$ D、 ${\begin{array}{l} x - y = 1 \\ y + \frac{1}{x} = 3 \end{array}$

查看试题解析
4. 若关于x ， y的二元一次方程组 ${\begin{array}{l} 2 x - y = 3 k + 4 \\ x + 4 y = 2 k - 5 \end{array}$ 的解满足 $x + y \leq \frac{4}{3}$ ，则k的取值范围是（）

A、 $k \leq 1$ B、 $k \leq 2$ C、 $k \leq - 1$ D、 $k \leq - 2$

查看试题解析
5. 用代入法解方程组 ${\begin{cases} y = 1 - x \\ x - 2 y = 4 \end{cases}$ 时，代入正确的是（）

A、x－2－x＝4 B、x－2－2x＝4 C、x－2＋2x＝4 D、x－2＋x＝4

查看试题解析
6. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - 2 y = 2 k \\ 2 x + y = k + 1 \end{array}$ ，以下结论： $①$ 当 $k = 2$ 时，方程组的解也是方程 $3 x + y = 5$ 的解； $②$ 存在实数 $k$ ，使得 $x + y = 0$ ； $③$ 不论 $k$ 取什么实数， $3 x + 4 y$ 的值始终不变； $④$ 若 $2 x + 3 y = 3$ ，则 $k = 8 .$ 其中正确的是（）

A、①②③ B、①②④ C、①③④ D、①④

查看试题解析
7. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，鸡兔各几何?"设鸡有 $x$ 只，兔有 $y$ 只，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 35 \\ 2 x + y = 94 \end{array}$ B、 ${\begin{array}{l} x + y = 35 \\ 2 x + 4 y = 94 \end{array}$ C、 ${\begin{array}{l} x + y = 35 \\ 4 x + 2 y = 94 \end{array}$ D、 ${\begin{array}{l} 2 x + 4 y = 35 \\ x + y = 94 \end{array}$

查看试题解析
8. 用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒、现有m张正方形纸板和n张长方形纸板，如果做两种纸盒若干个，恰好将纸板用完，则 $m + n$ 的值可能是（）

A、2025 B、2024 C、2023 D、2022

查看试题解析
9. 如图①，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长方形，如图②．这个拼成的长方形的长为30，宽为20，则图②中Ⅱ部分的面积是（）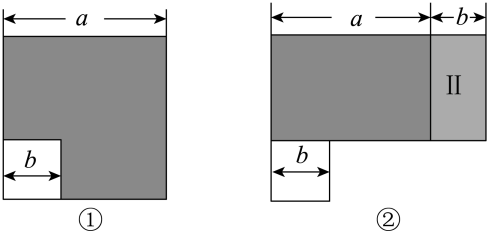

A、60 B、100 C、125 D、150

查看试题解析
10. 栖树一群鸦，鸦树不知数；三个坐一棵，五个地上落；五个坐一棵，闲了一棵树．请你动脑筋，鸦树各几何？歌谣大意是：一群乌鸦落在一片树上，如果三个乌鸦落在一棵树上，那么就有五个乌鸦没有树可落；如果五个乌鸦落在一棵树上，那么就有一棵树没有落乌鸦，请问乌鸦和树各多少？若设乌鸦有x只，树有y棵，由题意可列方程组（）

A、 ${\begin{array}{l} 3 y + 5 = x \\ 5 y - 1 = x \end{array}$ B、 ${\begin{array}{l} 3 y - 5 = x \\ 5 y = x - 1 \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} + 5 = y \\ 5 y = x - 5 \end{array}$ D、 ${\begin{array}{l} \frac{x - 5}{3} = y \\ \frac{x}{5} = y - 1 \end{array}$

查看试题解析
11. 将1，2，3，4，5，6，7，8，9，10这个10个自然数填到图中的10个格子里，每个格子中只填一个数，使得田字形的4个格子中所填数字之和都等于m．则m的最大值是（）

A、23 B、24 C、25 D、26

查看试题解析
12. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = 6 - 3 a \\ x - y = 6 a \end{array}$ ，给出下列说法：
①当 $a = 1$ 时，方程组的解也是 $x + y = a + 3$ 的解；
②若 $2 x + y = 3$ ，则 $a = - 1$ ；
③无论a取何值，x，y的值不可能互为相反数；
④x，y都为自然数的解有5对．
以上说法中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 非负数 $x$ ， $y$ 满足 $\frac{x - 1}{2} = \frac{2 - y}{3}$ ，记 $W = 3 x + 4 y$ ， $W$ 的最大值为 $m$ ，最小值 $n$ ，则 $m + n =$ ．

查看试题解析
14. 陕西全民阅读工作深入推进，书香社会建设进展明显，读书学习蔚然成风．某校为加强爱读书、读好书、善读书的阅读氛围，准备用720元购买图书展示架，可供选择的有A种展示架120元/个，B种展示架180元/个，在资金用尽且可以只买其中一种展示架的情况下，一共有种购买方案．

查看试题解析
15. 一组从小到大排列的数据：2，5，x，y，11，2x的平均数与中位数都是8，则 $x - y =$ ．

查看试题解析
16. 一个两位数数位上的数字之和是8，将它的十位数字和个位数字交换后，得到新的两位数，若新两位数比原两位数小18，则原两位数为．

查看试题解析
17. 用如图 $1$ 中的长方形和正方形纸板作侧面和底面，做成如图 $2$ 的竖式和横式两种无盖纸盒 $.$ 现在仓库里有 $1000$ 张正方形纸板和 $■$ 张长方形纸板 $.$ 若做了竖式纸盒 $x$ 个，横式纸盒 $y$ 个，恰好将库存的纸板用完 $.$ 小聪在做作业时，发现题中长方形纸板数字被墨水污染了，只记得这个数字比 $2000$ 略大些，是 $2001$ ， $2002$ ， $2003$ ， $2004$ ， $2005$ 中某个数字，则这个数字是，按照上述条件，最后做成的横式纸盒比竖式纸盒多个 $.$

查看试题解析
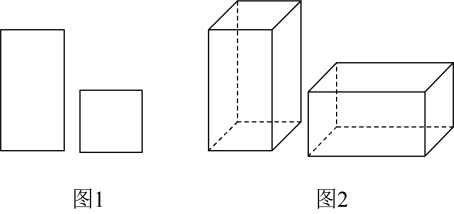18. 《孙子算经》中有这样一道题：今有木，不知长短．引绳度之，余绳四尺五，屈绳量之，不足一尺．问木长几何？大意是：用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条长度多一尺，则木条长尺．

查看试题解析
19. 我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念．如图是一个简单的二阶幻圆模型，若内外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等，则 $a =$ ； $b - c =$ ．

查看试题解析
20. 已知a ， b ， c为三角形的三边，且满足 $\sqrt{(2 a - 10)^{2}} + | b - 12 | + (13 - c)^{2} = 0$ ，这个三角形是三角形．

查看试题解析
21. 如图，在平面直角坐标系中，对正方形 $A B C D$ 及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数a，将得到的点先向右平移m个单位长度，再向上平移n个单位长度 $(m > 0 ， n > 0)$ ，得到正方形 $A^{'} B^{'} C^{'} D^{'}$ 及其内部的点，其中点A，B的对应点分别为 $A^{'}$ ， $B^{'}$ ．已知正方形 $A B C D$ 内部的一点F经过上述操作后得到的对应点 $F^{'}$ 与点F重合．

(1)、 $m =$ ， $n =$ ．

(2)、点F的坐标是．

查看试题解析
22. 对于一个三位数m，若其各个数位上的数字都不为0且互不相等，则称这样的数为“快乐数”．将“快乐数”m任意两个数位上的数字取出组成两位数，则一共可以得到6个两位数，将这6个两位数的和记为 $F (m)$ ．例如， $F (123) = 12 + 21 + 13 + 31 + 23 + 32 = 132$ ．记 $G (m) = \frac{F (m)}{22}$ ，则 $G (135) =$ ，若“快乐数”m满足百位上的数字是个位上数字的2倍，且 $G (m)$ 能被7整除，求满足条件的“快乐数”m的最大值为．

查看试题解析

三、计算题

23. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x + y = 2 \\ 8 x + 3 y = 9 \end{array}$ ；

(2)、 ${\begin{array}{l} 10 - 4 (x - 3) \geq 2 (x - 1) \\ x - 1 > \frac{1 - 2 x}{3} \end{array}$ ．

查看试题解析

四、解答题

24. 已知关于x ， y的方程组 ${\begin{array}{l} a x - 3 y = 17 \\ 5 x + b y = 4 \end{array}$ ，小明在解方程组时看错a ，解得 ${\begin{array}{l} x = - 2 \\ y = 7 \end{array}$ ，小红在解方程组时看错b ，解得 ${\begin{array}{l} x = 5 \\ y = 1 \end{array}$ ．

(1)、求a ， b的值．

(2)、求原方程组正确的解．

查看试题解析
25. “鸡兔同笼”是我国古代著名的数学趣题之一，大约在1500年前成书的《孙子算经》中就有“鸡兔同笼”的记载：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡兔关在一个笼子里，从上面数，有35个头；从下面数，有94条腿，问笼中各有几只鸡和兔？（要求列方程或方程组解应用题，否则不给分）

查看试题解析
26. 列方程组解应用题：
我国南宋数学家杨辉在《续古摘奇算法》中的攒九图中提出“幻圆”的概念．如图是一个最简的二阶幻圆的模型，将一些数字分别填入图中的圆圈内，要求：①外、内两个圆周上的四个数字之和相等；②外圆两直径上的四个数字之和相等，请你求出图中外，内两个圆周上两空白圆圈内应填写的数字是多少?

查看试题解析
27. 阅读材料：
我们知道方程组的解与方程组中每个方程的系数和常数项有联系，系数和常数项经过一系列变形、运算就可以求出方程组的解．因此，在现代数学的高等代数学科将系数和常数项排成一个矩阵的形式，规定：关于x ， y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 可以写成矩阵 $(\begin{array}{l} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array})$ 的形式．例如： ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$ 可以写成矩阵 $(\begin{array}{l} 3 & 4 & 16 \\ 5 & - 6 & 33 \end{array})$ 的形式．

根据以上信息解决下列问题：

(1)、请求出矩阵 $(\begin{array}{l} 4 & 1 & 5 \\ 3 & - 2 & 3 \end{array})$ 对应的方程组的解；

(2)、若矩阵 $(\begin{array}{l} a & - 2 & 3 & 7 \\ 1 & b & 4 & 5 \\ 2 & - 1 & c & 8 \end{array})$ 所对应的方程组的解为 ${\begin{array}{l} x = 1 \\ y = 1 \\ z = 1 \end{array}$ ，求 $a + b + c$ 的值．

查看试题解析

五、综合题

28. 小明与小乐两人共同计算 $(2 x + a) (3 x + b)$ .小明抄错为 $(2 x - a) (3 x + b)$ ，得到的结果为 $6 x^{2} - 13 x + 6$ ；小乐抄错为 $(2 x + a) (x + b)$ ，得到的结果为 $2 x^{2} - x - 6$ .

(1)、式子中的a，b的值各是多少?

(2)、请计算出原题的答案.

查看试题解析
29. 为加紧进行潮汕环线高速公路建设，现有大量的沙石需要运输．某工程队有载重量为8吨和12吨的卡车共12辆，全部车辆运输一次能运输124吨沙石．

(1)、求该工程队载重量为8吨和12吨的卡车各有多少辆？

(2)、为加快进度，该工程队需要一次运输沙石184吨以上，为了完成任务，准备新增购这两种卡车共6辆，工程队有几种购买方案？请一一写出来．

查看试题解析
30. 2023年4月23日是第28个“世界读书日”，长丰县图书馆举行了“阅来悦好书香长丰”阅读服务活动．为满足全县人民的读书需求，假设县图书馆计划采购社科图书和儿童读物两类图书．经了解，20本社科图书和40本儿童读物共需要1600元，20本社科图书比30本儿童读物多200元（注：所采购的社科图书价格都一样，所采购的儿童读物价格都一样）．

(1)、求每本社科图书和儿童读物各多少元．

(2)、若县图书馆要求购买社科图书和儿童读物总数不少于70本，其中儿童读物要比社科图书多20本，且总费用不超过2000元，请列出所有符合条件的购书方案．

查看试题解析
31. 五一假期，小序一家自驾从椒江出发，沿途到A地和B地游玩，已知从椒江到A地的高速公路里程为150公里，非高速公路里程为20公里，共耗油14升；从A地到B地的高速公路里程为100公里，非高速公路里程为40公里，共耗油12升．

(1)、分别求出小序家汽车在高速公路和非高速公路上平均每公里耗油各多少升；

(2)、今年9月23日杭州举行亚运会开幕式，小序一家想去观看，经查询发现从椒江到杭州的动车票是127元一张（假设小序一家所有人都需要购买动车票），从椒江到杭州的高速公路里程为240公里，非高速公路里程为28公里，如果自驾从椒江到杭州的费用由油费和高速公路过路费两部分组成，已知高速公路过路费为120元，预估油费为8元每升，请问小序一家至少有几人去杭州时选择自驾的费用更省？

查看试题解析
32. 现有甲乙两个工程队参加一条道路的改造施工，受条件限制，每天只能由一个工程队施工．若甲工程队先单独施工3天，再由乙工程队单独施工5天，则可以完成380米施工任务；若甲工程队先单独施工2天，再由乙工程队单独施工4天，则可以完成280米的施工任务．

(1)、求甲、乙两个工程队平均每天分别能完成多少米施工任务？

(2)、要改造的道路全长1800米，先由甲工程队先单独施工若干天，再由乙工程队单独完成剩下的施工任务，若工期不能超过40天，那么甲工程队至少要施工多少天？

查看试题解析
33. 新冠疫情期间，我市中学生积极行动起来，每人拿出自己一天的零花钱，筹款为贫困地区捐赠了32吨消毒液，并将消毒液运往该区．已知用3辆A型车和2辆B型车装满货物一次可运货17吨；用2辆A型车和3辆B型车装满货物一次可运货18吨．计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满消毒液．
根据以上信息，解答下列问题：

(1)、1辆A型车和1辆B型车都载满消毒液一次可分别运送多少吨？

(2)、若1辆A型车需租金200元/次，1辆B型车需租金240元/次．请设计租车方案，并选出最省钱的租车方案及最少租金．

查看试题解析
34. 为加强中小学生安全教育，某校组织了“防溺水、交通安全”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格也相同），购买2个足球和3个篮球共需374元；足球单价是篮球单价的2倍少9元．

(1)、请用方程组求足球和篮球的单价各是多少元？

(2)、根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，则学校最多可以购买多少个足球？

查看试题解析
35.

(1)、解决问题：有48支队520名运动员参加男子篮球和女子排球比赛，其中每支男子篮球队10人，每支女子排球队12人，男子篮球、女子排球队各多少支参赛？

(2)、问题拓展：若有a支球队参加男子篮球比赛，b支球队参加女子排球比赛，其中每支男子篮球队m人，每支女子排球队n人，则参加篮球比赛和参加排球比赛的队员共有人．

查看试题解析
36. 某商店销售A、B、C三种型号的饮料．随着夏季来临，天气逐渐炎热，该商店决定从今年5月1日起将A饮料每瓶的价格上调20%，将B饮料每瓶的价格下调10%，C饮料价格不变，是每瓶7元，已知调价前A、B、C三种饮料各买一瓶共花费18元，调价后买A饮料2瓶、B饮料5瓶共花费39元．

(1)、问A、B两种饮料调价前的单价；

(2)、今年6月份，温州某单位花费3367元在该商店购买A、B、C三种饮料共n瓶，其中购得B饮料的瓶数是A饮料的2倍，求n的最大值．

查看试题解析