中考数学第一轮复习：一元一次方程

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 如果方程 $x^{2 n - 5} - 2 = 0$ 是关于x的一元一次方程，则n的值为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 若关于 $x$ 的方程 $x^{2} - 2 x + k - 1 = 0$ 有实数根，则 $k$ 的取值不可以是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 由m=4-x，m=y-3，可得出x与y的关系是（　）

A、x+y=7 B、x+y=-7 C、x+y=1 D、x+y=-1

查看试题解析
4. 在解方程 $3 x + 5 = - 2 x - 1$ 的过程中，移项正确的是（）

A、 $3 x - 2 x = - 1 + 5$ B、 $- 3 x - 2 x = 5 - 1$ C、 $- 3 x - 2 x = - 5 - 1$ D、 $3 x + 2 x = - 1 - 5$

查看试题解析
5. 《九章算术》中记载这样一道题：今有牛、马、羊食人苗．苗主责之粟五斗，羊主曰：“我羊食半马．”马主曰：“我马食半牛．”大意是：现在有一头牛、一匹马、一只羊吃了别人家的禾苗，禾苗的主人要求这些动物的主人共计赔偿五斗粟米．羊的主人说：“我家羊只吃了马吃的禾苗的一半．”马的主人说：“我家马只吃了牛吃的禾苗的一半．”按此说法，羊的主人应当赔偿禾苗的主人多少斗粟米？（　　）

A、 $\frac{5}{7}$ B、 $\frac{4}{7}$ C、 $\frac{3}{7}$ D、 $\frac{2}{7}$

查看试题解析
6. 为了准备期末检测评价，小军去文具店购买了数支单价为2元的笔芯和若干块单价为k元的橡皮（k为正整数），共花费了6元，已知购买笔芯数量是橡皮数量的2倍，则小军购买的笔芯的数量为（）

A、1支 B、2支 C、3支 D、4支

查看试题解析
7. 规定：对于任意实数x，通常用[x]表示不超过x的最大整数，如：[π]=3，[2]=2，[-2.1]=-3给出下列结论：①[-x]=-x；②若[x]=n，则x的取值范围是n≤x<n+1；③当-1<x<1时，[1+x]+[1-x]的值为1或2；④x=-2.75是方程4x-2[x]+5=0的唯一解．其中正确结论的序号是（）

A、①② B、②③ C、①③ D、③④

查看试题解析
8. 在平面直角坐标系中有 $A$ ， $B$ ， $C$ 三点，且点 $A (a ， 0)$ ，点 $B (0 ， b)$ ，点 $C (0 ， c)$ ，若 $3 a + 2$ 的立方根是 $2$ ， $3 a - b - 1$ 的算术平方根为 $3$ ， $c$ 是比 $\sqrt{2}$ 小的最大整数，则下列结论：
① $a = 2 c$ ；

② $\sqrt{- 2 a b c}$ 的平方根为 $\pm 4$ ；

③ $O A = 2 O B$ ；

④c是关于 $x$ 的方程 $a x + b = 0$ 的解；

⑤若线段 $C E ∥ A O$ ，且 $C E = A O$ ，则点 $E$ 的坐标为 $(a ， c)$ 或 $(\frac{b}{2} ， c)$ ．

其中正确的个数有（　　）

A、5个 B、4个 C、3个 D、2个

查看试题解析
9. 如图，点A在数轴上表示的数是-8，点B在数轴上表示的数是16．若点A以6个单位长度/秒的速度向右匀速运动，同时点B以2个单位长度/秒的速度向左匀速运动．问：当AB＝8时，运动时间为多少秒？（）

A、2秒 B、13.4秒 C、2秒或4秒 D、2秒或6秒

查看试题解析
10. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术，其中方程术是其最高的代数成就．《九章算术》中有这样一个问题：“今有善行者行一百步，不善行者行六十步．今不善行者先行一百步，善行者追之，问几何步及之？”译文：“相同时间内，走路快的人走100步，走路慢的人只走60步．若走路慢的人先走100步，走路快的人要走多少步才能追上？(注：步为长度单位)”设走路快的人要走x步才能追上，根据题意可列出的方程（）
60

A、x=100- $\frac{60}{100}$ x B、x=100+ $\frac{60}{100}$ x C、 $\frac{100}{60}$ x=100+x D、 $\frac{100}{60}$ x=100-x

查看试题解析
11. 方程 $| x | + | x - 2022 | = | x - 1011 | + | x - 3033 |$ 的整数解共有（）

A、1010 B、1011 C、1012 D、2022

查看试题解析
12. 已知正整数a，b，c，d满足 $a < b < c < d$ ，且 $a + b + c + d = d^{2} - c^{2} + b^{2} - a^{2}$ ，关于这个四元方程下列说法正确的个数是（）
① $a = 1$ ， $b = 2$ ， $c = 3$ ， $d = 4$ 是该四元方程的一组解；
②连续的四个正整数一定是该四元方程的解；
③若 $a < b < c < d < 10$ ，则该四元方程有21组解；
④若 $a + b + c + d = 2022$ ，则该四元方程有504组解．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 王勇买了一张

30

元的租书卡，每租一本书后卡中剩余金额

y

（元）与租书本数

x

（本）之间的关系式为.

租书数 $/$ 本	卡中余额 $/$ 元
$1$	$30 - 0.8$
$2$	$30 - 1.6$
$3$	$30 - 2.4$
……	……

查看试题解析

14. 在直角三角形中，一个锐角比另一个锐角小 $10 °$ ，则较大的锐角的大小是．

查看试题解析
15. 斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路．某人行横道全长24米，小明以 $1.2 m / s$ 的速度过该人行横道，行至 $\frac{1}{3}$ 处时，9秒倒计时灯亮了．小明要在红灯亮起前通过马路，他的速度至少要提高到原来的倍．

查看试题解析
16. 某多边形内角和是外角和的2倍，则该多边形的边数.

查看试题解析
17. 为保证安全，某两段铁路 $M N ， P Q$ 两旁安置了两座可旋转探照灯A，B，探照灯的光线可看作射线如图，灯A的光线 $A C$ 从射线 $A M$ 开始，绕点A顺时针旋转至射线 $A N$ 上便立即回转，灯B光线 $B D$ 从射线 $B P$ 开始，绕点B顺时针旋转至射线 $B Q$ 便立即回转，两灯不停交叉照射巡视．已知 $P Q ∥ M N$ ，连接 $A B$ ， $∠ B A M ： ∠ B A N = 2 ： 1$ ，则 $∠ B A N =$ $°$ ；若灯B的光线先转动，每秒转动 $1 °$ ， 45秒后灯A的光线才开始转动，每秒转动 $2 °$ ，在灯B的光线第一次到达 $B Q$ 之前，灯A的光线转动秒时，两灯的光线互相平行．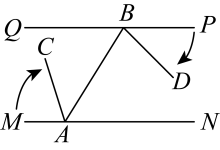

查看试题解析
18. $[a]$ 表示不大于a的最大整数，例如 $[- 2.3] = - 3 ， [2.5] = 2 ， [3] = 3$ ，那么方程 $[2 x + 1] = 3 x - 1$ 的解是．

查看试题解析
19. 若 $| a - 3 | + | a + 2 | = 6$ ，则a= ．

查看试题解析
20. 如图1所示，已知甲、乙为两把不同刻度的直尺，且同一把直尺上的刻度之间距离相等，小研将此两把直尺紧贴，并将两直尺上的刻度0彼此对准后，发现甲尺的刻度36会对准乙尺的刻度48．

(1)、如图2，若将甲尺向右平移且平移过程中两把直尺维持紧贴，使得甲尺的刻度0对准乙尺的刻度4，则此时甲尺的刻度21会对准乙尺的刻度是；

(2)、如图3，若将甲尺向右平移且平移过程中两把直尺维持紧贴，使得甲尺的刻度0会对准乙尺的刻度m，如图3所示，则此时甲尺的刻度n会对准乙尺的刻度是．（用含m，n的式子表示）

查看试题解析
21. 阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是【A，B】的好点．

(1)、如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是【A，B】的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D【A，B】的好点，但点D【B，A】的好点．（请在横线上填是或不是）

(2)、知识运用：
如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为-2．数所表示的点是【M，N】的好点；

(3)、如图3，A、B为数轴上两点，点A所表示的数为-20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过秒时，P、A和B中恰有一个点为其余两点的好点？

查看试题解析

22. 下表是某市居民出行方式以及收费标准：（不足1千米按1千米算）

打车方式	出租车	3千米以内8元；超过3千米的部分2.4元/千米
打车方式	滴滴快车	路程：1.4元/千米；时间：0.6元/分钟
说明	打车的平均车速40千米/时

假设乘坐8千米，耗时：8÷40×60＝12分钟；出租车收费：8＋（8－3）×2.4＝20元；滴滴快车收费：8×1.4＋12×0.6＝18.4元．

为了提升市场竞争力，出租车公司推出行使里程超过10千米立减4.8元活动．小聪乘坐出租车从甲地到达乙地支付车费22.4元，若改乘滴滴快车从甲地到乙地，则需支付元．

查看试题解析

三、计算题

23. 解方程： $x - 2 (2 - x) = 8$

查看试题解析
24. 按要求计算下列各题

(1)、解方程： $\frac{x - 3}{2} - \frac{2 x + 1}{3} = 1$

(2)、求不等式组 ${\begin{array}{l} 2 - 3 x > - 2 x \\ 4 + \frac{x}{2} > \frac{5}{2} \end{array}$ 的所有整数解．

查看试题解析

四、综合题

25. 先阅读绝对值不等式 $| x | < 6$ 和 $| x | > 6$ 的解法，再解答问题．
①因为 $| x | < 6$ ，从数轴上（如图1）可以看出只有大于 $- 6$ 而小于6的数的绝对值小于6，所以 $| x | < 6$ 的解集为 $- 6 < x < 6$ ．
②因为 $| x | > 6$ ，从数轴上（如图2）可以看出只有小于 $- 6$ 的数和大于6的数的绝对值大于6．所以 $| x | > 6$ 的解集为 $x < - 6$ 或 $x > 6$ ．

(1)、 $| x | < 2$ 的解集为， $| x | > 5$ 的解集为；

(2)、已知关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} 2 x - y = 9 m + 4 \\ x + 4 y = - 8 m + 2 \end{array}$ 的解满足 $| x + y | \leq 3$ ，其中 $m$ 是负整数，求 $m$ 的值．

查看试题解析
26. 某地计划修建一条长36千米的乡村公路，已知甲工程队修路的速度是乙工程队修路速度的 $1.5$ 倍，乙工程队单独完成本次修路任务比甲工程队单独完成多20天．

(1)、求甲、乙两个工程队每天各修路多少千米？

(2)、已知甲工程队修路费用为25万元/千米，乙工程队修路费用为20万元/千米．甲工程队先单独修路若干天后，接到其它任务需要离开，剩下的工程由乙工程队单独完成．若要使修路总时间不超过55天，总费用不超过820万元，且甲工程队所修路程需为整数，请问共有几种修路方案？哪种方案最省钱？

查看试题解析
27. 某商场第1次用39万元购进 $A$ ， $B$ 两种商品，销售完后获得利润6万元，它们的进价和售价如表（总利润=单价利润×销售量）：

价格商品

进价（元/件）

售价（元/件）

$A$

1200

1350

$B$

1000

1200

(1)、该商场第1次购进 $A$ ， $B$ 两种商品各多少件？

(2)、商场第2次以原进价购进 $A$ ， $B$ 两种商品，购进 $A$ 商品的件数不变，而购进 $B$ 商品的件数是第1次的2倍， $A$ 商品按原售价销售，而 $B$ 商品打折销售，若两种商品销售完毕，要使得第2次经营活动获得利润等于5.4万元，则 $B$ 种商品是按几折销售的？

查看试题解析
28. 我校举行数学竞赛，一共有25道题，满分100分，每答对一题得4分，答错扣一分，不答记0分。

(1)、某同学只有一道题未作答，最后得分86分，则该生一共答对多少题?

(2)、若规定参赛者每题必须作答，得分大于或等于90分，才可以评为一等奖，则参赛者至少答对多少题才能获评一等奖?

查看试题解析

29. “闪送”是

1

小时同城速递服务领域的开拓者和一对一急送服务标准的制定者．客户下单后，订单全程只由唯一的“闪送员”专门派送，平均送达时间在

60

分钟以内，同时避免传统快递服务的中转、分拣、配送过程当中存在的诸多安全性问题．某闪送公司每月给闪送员的工资为：底薪

2000

元，超过

300

单后另加送单补贴（每送一个包裹称为一个单），送单补贴的具体方案如下：

送单数量	补贴（元/单）
每月超过 $300$ 单且不超过 $500$ 单的部分	$5$
每月超过 $500$ 单的部分	$7$

(1)、若某月甲﹑乙两位闪送员分别送了

450

单和

580

单，你能帮忙算算他们分别可以拿到多少工资？

(2)、设闪送员小金在

6

月份送了

x

单（

x > 300

），所得工资为

y

元，则

y

与

x

的函数关系式是什么？

(3)、如果小金想在

7

月份获得不低于

4000

元的工资，他至少需要送多少单才能完成目标？

查看试题解析

30. 某公司要生产若干件新产品，需要精加工后，才能投放市场．现在甲、乙两个加工厂都想加工这批产品，已知甲工厂单独加工这批产品比乙工厂单独加工这批产品多用20天，甲工厂每天可加工16件产品，乙工厂每天可加工24件产品．

(1)、求这个公司要加工新产品的件数．

(2)、在加工过程中，公司需支付甲工厂每天加工费80元，乙工厂每天加工费120元．公司还需另派一名工程师每天到厂家进行技术指导，并负担每天5元的午餐补助费．公司制定产品加工方案如下：可由一个工厂单独加工完成，也可由两个工厂合作同时完成．当两个工厂合作时，这名工程师轮流去这两个工厂．请你通过计算帮助公司从所有可供选择的方案中选择一种既省钱，又省时间的加工方案．

查看试题解析
31. 列方程解应用题：
暑假，某校七年级（1）班组织学生去公园游玩，该班有50名同学组织了划船活动，如图是划船须知.他们一共租了10条船，并且每条船都坐满了人，

(1)、大、小船各租了几条？

(2)、他们租船一共花了多少元钱？

查看试题解析

价格商品	进价（元/件）	售价（元/件）
$A$	1200	1350
$B$	1000	1200