中考数学第一轮复习：二次根式

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列式子中，是二次根式的是（）

A、 $- \sqrt{6}$ B、 $\sqrt[3]{6}$ C、 $\sqrt{x}$ D、 $\sqrt{- 6}$

查看试题解析
2. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是 $($ $)$

A、x<1 B、x≤1 C、x>1 D、x≥1

查看试题解析
3. 若实数 $a$ ， $b$ 满足 $\sqrt{a - 2} + | b + 3 | = 0$ ，则 $b^{a}$ 的值是（）

A、 $- 3$ B、3 C、 $- 9$ D、9

查看试题解析
4. 下列计算正确的是(　　)

A、 $2 \sqrt{3} + 4 \sqrt{2} = 6 \sqrt{5}$ B、 $\sqrt{8} = 4 \sqrt{2}$ C、 $\sqrt{27} \div \sqrt{3} = 3$ D、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$

查看试题解析
5. 下列式子中，最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{7}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
6. 下列二次根式中，能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
7. 按如图所示运算程序，输入 $x = - \sqrt{2}$ ， $y = - 2 \sqrt{2}$ ，则输出结果为（）

A、 $- 6$ B、6 C、 $- \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
8. 下列算式的计算结果不为0的是（）

A、 $- 2 + \sqrt{{(- 2)}^{2}}$ B、 $- 2 + \sqrt[3]{- 8}$ C、 $- 2 + {(- \sqrt{2})}^{2}$ D、 ${(\sqrt{2})}^{2} - \sqrt{2^{2}}$

查看试题解析
9. 下列各式计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt{3} + \sqrt{12} = \sqrt{15}$ C、 $\sqrt{a^{2}} = a$ D、 $2 \sqrt{a} - \sqrt{4 a} = 0$

查看试题解析
10. 记 $S_{n} = \sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \dots + \sqrt{1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}}$ ，则 $\frac{S_{2016}}{2016} =$ （）

A、 $\frac{2016}{2017}$ B、 $\frac{2017}{2016}$ C、 $\frac{2017}{2018}$ D、 $\frac{2018}{2017}$

查看试题解析
11. 与 $\sqrt{18}$ -3最接近的整数是（）

A、4 B、3 C、2 D、1

查看试题解析
12. 已知a= $\frac{1}{\sqrt{2} + 1}$ ，b= $\frac{1}{\sqrt{2} - 1}$ ，则a与b的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、平方值相等

查看试题解析

二、填空题

13. 当 $x = 5$ 时，二次根式 $\sqrt{x - 3}$ 的值是．

查看试题解析
14. 如果式子 $\sqrt{x - 7}$ 有意义，则 $x$ 的取值范围为．

查看试题解析
15. 已知： $m^{2} < \sqrt{21}$ ，若 $\sqrt{m + 2}$ 是整数，则 $m^{2} - 1 =$ ．

查看试题解析
16. 请写出一个能与 $\sqrt{18}$ 合并的最简二次根式，你的答案是．

查看试题解析
17. 若最简二次根式 $\sqrt[m - 1]{7}$ 与最简二次根式 $\sqrt{4 n - 1}$ 是同类二次根式，则 $m + n =$ ．

查看试题解析
18. 计算 $\sqrt{63} - 7 \sqrt{\frac{1}{7}}$ 的结果是．

查看试题解析
19. 若 $\sqrt{x - 2023} + \sqrt{y + 2023} = 2$ ，其中 $x$ ， $y$ 均为整数，则 $x + y =$ ．

查看试题解析
20. $\sqrt{5 n}$ 为整数，则正整数n的最小值为．

查看试题解析

三、计算题

21. 计算： $\sqrt{\frac{1}{6}} \times \sqrt{96} \div \sqrt{6}$

查看试题解析
22. 计算： $\sqrt{9} + \sqrt{8} - 4 \sqrt{\frac{1}{2}}$

查看试题解析
23. 解决如下问题：

(1)、分母有理化： $\frac{1}{\sqrt{2} + 1}$ ．

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2025} + \sqrt{2024}}$ ．

(3)、若a＝ $\frac{1}{\sqrt{5} - 2}$ ，求2a²-8a+1的值．

查看试题解析
24.

(1)、计算： $\sqrt{12} \times (\sqrt{75} + 3 \sqrt{\frac{1}{3}} - \sqrt{48})$

(2)、解方程 $x^{2} - 4 x - 5 = 0$

查看试题解析
25. 先化简，再求值： $\sqrt{4 a^{4}} - (a + \sqrt{2}) (a - \sqrt{2})$ ，其中 $a = \frac{\sqrt{3}}{3}$ ．

查看试题解析
26. 计算： $(\sqrt{3} + 1) \times (\sqrt{3} - 1) + \sqrt{48} + {(π - 1)}^{0} + {(- \frac{1}{3})}^{- 1}$ ．

查看试题解析

四、解答题

27. 如图，木工师傅在一块矩形木料上截出两块面积分别为 $18 d m^{2}$ 和 $32 d m^{2}$ 的正方形木板．

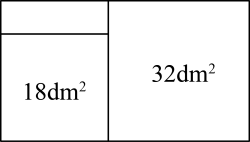(1)、截出的两块正方形木板中，小正方形木板的边长为dm，大正方形木板的边长为dm；（填最简二次根式）

(2)、求原矩形木料的面积；

(3)、木工师傅想从剩余矩形木料中截出一块正方形木板，这块正方形木板的边长为2dm．（填“能”或“不能”）

查看试题解析
28. 如图，已知 $B$ 地在 $A$ 地的正东方向，两地相距 $28 \sqrt{2} k m ， A ， B$ 两地之间有一条东北走向的高速公路，且A，B两地到这条高速公路的距变相等.上午8：00测得一辆在高速公路上行驶的汽车位于 $A$ 地的正南方向 $P$ 处，至上午8：20，发现该车在 $B$ 地的西北方向 $Q$ 处，该段高速公路限速为110km/h，判断该车是否超速行驶.

查看试题解析
29. 若 $\frac{| 16 - a^{2} | + \sqrt{a + 4 b}}{a + 4} = 0$ ，则 $a^{b}$ 的平方根．

查看试题解析
30. 若 $[x]$ 表示不超过x的最大整数（如 $[π] = 3 ， [- 2 \frac{2}{3}] = - 3$ 等），求 $[\frac{1}{2 - \sqrt{1 \times 2}}] + [\frac{1}{3 - \sqrt{2 \times 3}}]$ $+ [\frac{1}{3 - \sqrt{2 \times 3}}] + \dots + [\frac{1}{2014 - \sqrt{2013 \times 2014}}]$ 的值．

查看试题解析
31. 已知 $\frac{1}{1 \sqrt{2} + 2 \sqrt{1}}$ + $\frac{1}{2 \sqrt{3} + 3 \sqrt{2}}$ + $\frac{1}{3 \sqrt{4} + 4 \sqrt{3}}$ +…+ $\frac{1}{n \sqrt{n + 1} + (n + 1) \sqrt{n}}$ ＝ $\frac{49}{50}$ ，求n的值.

查看试题解析

五、综合题

32. 如图，在平面直角坐标系中，已知 $A (0 ， a)$ ， $B (b ， 0)$ ， $C (4 ， c)$ 三点，其中 $a 、 b 、 c$ 满足关系式： $| a - 3 | + {(b - 4)}^{2} + \sqrt{c - 5} = 0$ ．

(1)、求 $a 、 b 、 c$ 的值；

(2)、请直接判断 $B C$ 与y轴的位置关系；

(3)、若平面内有一点 $P (m ， \frac{1}{3})$ ，且点P到 $B C$ 的距离为5，请求出 $△ A O P$ 的面积；

(4)、如果点 $P (m ， \frac{1}{3})$ 在第二象限内，是否存在负整数m ，使四边形 $A B O P$ 的面积不小于 $△ A O P$ 面积的3倍？若存在，请直接写出所有满足条件的点P的坐标，若不存在，请说明理由．

查看试题解析
33. 观察下列等式及验证，解答后面的问题：
第1个等式： $\sqrt{2 + \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ，验证： $\sqrt{2 + \frac{2}{3}} = \sqrt{\frac{8}{3}} = 2 \sqrt{\frac{2}{3}}$ ；

第2个等式： $\sqrt{3 + \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ，验证： $\sqrt{3 + \frac{3}{8}} = \sqrt{\frac{27}{8}} = 3 \sqrt{\frac{3}{8}}$ ；

第3个等式： $\sqrt{4 + \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ，验证： $\sqrt{4 + \frac{4}{15}} = \sqrt{\frac{64}{15}} = 4 \sqrt{\frac{4}{15}} ， ⋯$ ．

(1)、请写出第4个等式，并验证；

(2)、按照以上各等式反映的规律，猜想第 $n - 1$ 个 $(n$ 为正整数，且 $n \geq 2)$ 等式，并通过计算验证你的猜想．

查看试题解析
34. 阅读材料：像 $(\sqrt{3} + 1) (\sqrt{3} - 1) = 2$ ， $\sqrt{a} \times \sqrt{a} = a (a \geq 0)$ …这种两个含二次根式的代数式相乘，积不含二次根式，我们称这两个代数式互为有理化因式．在进行二次根式运算时，利用有理化因式可以化去分母中的根号．
例如： $\frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{2 \sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{4}$ ； $\frac{\sqrt{3} + 1}{\sqrt{3} - 1} = \frac{(\sqrt{3} + 1)}{(\sqrt{3} - 1) (\sqrt{3} + 1)} = 2 + \sqrt{3}$ ．
解答下列问题：

(1)、 $\sqrt{6}$ 的有理化因式是， $\sqrt{3} + 2$ 的有理化因式是．

(2)、观察下面的变形规律，请你猜想： $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ．
$\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ， $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ …

(3)、利用上面的方法，请化简：
$\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + ⋯ ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2023}}$ ．

查看试题解析