中考数学第一轮复习：分式

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列各式： $\frac{1}{x}$ ， $\frac{1}{2} (x + y)$ ， $\frac{x}{π}$ ， $\frac{2}{x - y}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 函数 $y = \frac{1}{x + 2}$ 中自变量 $x$ 的取值范围是（）

A、 $x > - 2$ B、 $x \neq - 2$ C、 $x = - 2$ D、 $x \geq - 2$

查看试题解析
3. 分式 $\frac{x^{2} - 25}{x + 5}$ 的值是零，则 $x$ 的值为（）

A、5 B、 $\pm 5$ C、 $- 5$ D、 $\pm \sqrt{5}$

查看试题解析
4. 下列分式中，是最简分式的是（）

A、 $\frac{x y}{2 x^{2}}$ B、 $\frac{x - 1}{x^{2} - 1}$ C、 $\frac{x + y}{x}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
5. 要把分式方程 $\frac{3}{2 x - 4} = \frac{1}{x}$ 化为整式方程，方程两边要同时乘以（）

A、 $x$ B、 $2 x - 4$ C、 $2 (x - 2)$ D、 $2 x (x - 2)$

查看试题解析
6. 计算 $\frac{3}{a} + \frac{2}{a}$ 的结果为（）

A、 $\frac{1}{a}$ B、 $\frac{6}{a^{2}}$ C、 $\frac{5}{a}$ D、 $\frac{6}{a}$

查看试题解析
7. 2023年4月24日中国航天日在合肥盛大举行，大会以“格物致知，叩问苍穹”为主题，展示了中国航天领域的最新成果．当前航天器测距精度已达0.0000002毫米，该数用科学记数法表示为（）

A、 $2 \times 1 0^{- 7}$ B、 $0.2 \times 1 0^{- 7}$ C、 $2 \times 1 0^{- 8}$ D、 $0.2 \times 1 0^{- 8}$

查看试题解析
8. 下列说法中：①若 $a^{m} = 6 ， a^{n} = 3$ ，则 $a^{m - n} = 2$ ；②若 $a + b = 3 ， a b = 2$ ，则 $\frac{b}{a} + \frac{a}{b} = \frac{9}{2}$ ；③若 $(t - 2)^{2 t} = 1$ ，则 $t = 3$ 或 $t = 0$ ；④若方程组 ${\begin{array}{l} x + y = 6 \\ m x + y = 4 \end{array}$ 的解也是方程组 $x - 3 y = - 2$ 的解，则 $m = 2$ ；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．下列判断正确的是（）

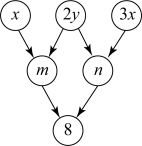
结论 Ⅰ ：若n的值为5，则y的值为1；

结论Ⅱ： $x + y$ 的值为定值；

结论Ⅲ：若 $x^{m - 3 n} = 1$ ，则y的值为4或1．

A、Ⅰ ，Ⅲ均对 B、Ⅱ对，Ⅲ错 C、Ⅱ错，Ⅲ对 D、Ⅰ ，Ⅱ均错

查看试题解析
10. 下列说法中：①若 $a^{m} = 6$ ， $a^{n} = 3$ ，则 $a^{m - n} = 2$ ；②两条直线被第三条直线所截，一组内错角的角平分线互相平行；③若 $(t - 2)^{2 t} = 1$ ，则 $t = 3$ 或 $t = 0$ ；④已知二元一次方程组 ${\begin{array}{l} x + y = 6 \\ a x + y = 4 \end{array}$ 的解也是二元一次方程 $x - 3 y = - 2$ 的解，则a的值是0.5；其中正确的是（）

A、①② B、②③ C、①④ D、③④

查看试题解析
11. 若 $a$ ， $b$ 为实数且满足 $a \neq - 1$ ， $b \neq - 1$ ，设 $M = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $N = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，有以下2个结论： $①$ 若 $a b = l$ ，则 $M = N$ ； $②$ 若 $a + b = 0$ ，则 $M N \leq 0 .$ 下列判断正确的是（）

A、①对②错 B、①错②对 C、①②都错 D、①②都对

查看试题解析
12. 下列结论中： ①若 ${(1 - x)}^{x + 1} = 1$ ，则 $x = - 1$ ；②若 $a^{2} + b^{2} = 3 ， a - b = 1$ ，则 $(2 - a) (2 - b)$ 的值为 $5 - 2 \sqrt{5}$ ； ③若规定：当 $a b \neq 0$ 时， $a \otimes b = a + b - a b$ ，若 $a \otimes (4 - a) = 0$ ，则 $a = 2$ ；④若 $4^{x} = a ， 8^{y} = b$ ，则 $2^{4 x - 3 y}$ 可表示为 $\frac{2 a}{b}$ ； ⑤若 $(x + 1) (x - a)$ 的运算结果中不含 $x$ 的一次项，则 $a = 1$ . 其中正确的个数是（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 已知n为整数，当 $n =$ 时，分式 $\frac{2}{n - 1}$ 的值是整数．

查看试题解析
14. 已知分式 $\frac{2 a}{a + b} = 3$ ，若把a，b的值都扩大到原来的3倍，此时分式的值为（填数字）

查看试题解析
15. 分式： $\frac{1}{4 a}$ ， $\frac{2}{3 b^{2}}$ ， $\frac{1}{2 a b}$ 的最简公分母是．

查看试题解析
16. 如图，一个长为l，宽为a的长方形内，铺满了一层半径为r的圆，则长方形的面积利用率（圆形总面积与长方形面积的比）为（结果保留 $π$ ）．

查看试题解析
17. 计算： $\frac{1}{x - 1} + \frac{3}{x - 1} =$ ．

查看试题解析
18. 计算： $202 3^{0} + {(\frac{1}{3})}^{- 1} =$ ．

查看试题解析
19. 若 ${(5 - 2 x)}^{x + 1} = 1$ ，则 $x =$ ．

查看试题解析
20. 当 $x$ 分别取值 $\frac{1}{2020} ， \frac{1}{2019} ， \frac{1}{2018} ， \frac{1}{2017} ， ⋯ ， \frac{1}{2} ， 0 ， 1 ， 2 ， ⋯ ， 2017 ， 2018 ， 2019 ， 2020$ 时，计算代数式 $\frac{x^{2} - 1}{3 x^{2} + 3}$ 的值，将所得结果相加，其和等于．

查看试题解析
21. 若 $a^{3} + 3 a^{2} + a = 0$ ，则 $\frac{2022 a^{2}}{a^{4} + 2015 a^{2} + 1} =$ ．

查看试题解析
22. 欧拉是18世纪瑞士著名的数学家，他的贡献不仅遍及高等数学的各个领域，在初等数学中也留下了他的足迹．下面是关于分式的欧拉公式：
$\frac{a^{r}}{(a - b) (a - c)} + \frac{b^{r}}{(b - c) (b - a)} + \frac{c^{r}}{(c - a) (c - b)} = {\begin{cases} p ， & r = 0 时 \\ 0 ， & r = 1 时 \\ 1 ， & r = 2 时 \\ a + b + c ， & r = 3 时 \end{cases}$

（其中a，b，c均不为零，且两两互不相等）．

(1)、当 $r = 0$ 时，常数p的值为．

(2)、利用欧拉公式计算： $\frac{202 2^{3}}{2} - 202 1^{3} + \frac{202 0^{3}}{2} =$ ．

查看试题解析

三、计算题

23. 先化简，再求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - x}{x^{2} - 4}$ ，其中 $x = - 3$ ．

查看试题解析
24. 先化简，再求值： $\frac{a^{2} - 1}{a^{2} + 2 a} \div \frac{a - 1}{a} - \frac{a}{a + 2}$ ，其中 $a$ 为整数，且满足 $0 < a < \sqrt{5}$ ．

查看试题解析
25. 计算： $(- 1)^{2023} + (π - 3)^{0} - {(- \frac{1}{2})}^{- 2}$ ．

查看试题解析
26. 已知 $| a b + 2 | + | a + 1 | = 0$ ，求下列式子的值： $\frac{1}{(a - 1) (b + 1)} + \frac{1}{(a - 2) (b + 2)} + \dots + \frac{1}{(a - 2018) (b + 2018)}$

查看试题解析
27. 已知 $a + b + c = 0$ ，且 $a b c \neq 0$ ，求： $a (\frac{1}{b} + \frac{1}{c}) + b (\frac{1}{a} + \frac{1}{c}) + c (\frac{1}{a} + \frac{1}{b})$ 的值.

查看试题解析
28. 设 $\frac{x}{x^{2} + x + 1}$ ＝a(a≠0)，求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值．

查看试题解析

四、综合题

29. 已知 $x = 2 - \sqrt{3}$ ， $y = 2 + \sqrt{3}$ ，求下列代数式的值：

(1)、 $x^{2} - y^{2}$ ；

(2)、 $\sqrt{\frac{y}{x}} + \sqrt{\frac{x}{y}}$ ．

查看试题解析

30. 阅读下列材料，完成相应的任务．

真分式与假分式

将两个整数相除（除数不为零）表示成分数，可能得到真分数，也可能得到假分数；类似地，分式也有真、假之分．我们规定，在分式中，当分子中整式的次数大于或等于分母中整式的次数，如 $\frac{x^{2} - 1}{x}$ ， $\frac{2 x^{2} + 1}{x^{2} - x}$ ，称为假分式；当分子中整式的次数小于分母中整式的次数时，如 $\frac{3}{x + 1}$ ， $\frac{x^{2} - 1}{x^{3} + 2 x - 3}$ ，称为真分式．

一些假分数可以化为带分数，即整数与真分数之和，如： $\frac{7}{3} = \frac{2 \times 3 + 1}{3} = 2 + \frac{1}{3} = 2 \frac{1}{3}$ ；类似地，我们也可以把一些假分式化为带分式，即整式与真分式之和（或差）的形式．例： $\frac{x^{2} - 1}{x} = \frac{x^{2}}{x} - \frac{1}{x} = x - \frac{1}{x}$ ； $\frac{2 x^{2} + 1}{x^{2} - x} = \frac{2 (x^{2} - x) + 2 x + 1}{x^{2} - x} = 2 + \frac{2 x + 1}{x^{2} - x}$ ．

任务：

(1)、下列分式中，是假分式（填序号）：

① $\frac{m^{2} + m}{2 m^{2} - 3}$ ；② $\frac{3}{x^{2}}$ ；③ $\frac{x^{3} - 3 x^{2} + 3}{5 x^{2} - 2 x}$ ；

(2)、小彬将一个假分式化成带分式的结果为

x + 1 + \frac{2 x + 1}{x - 1}

，请求出原来的假分式；

(3)、请从下面

A ， B

两题中任选一题作答．我选择． A.将假分式

\frac{2 x - 1}{x + 1}

化成带分式的结果为；B.将假分式

\frac{3 x^{2} - 1}{x - 1}

化成带分式的结果为 ▲ ．

查看试题解析

31. 阅读以下内容，完成问题．

解： $1 - \frac{x - y}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}}$

$= \frac{x + 2 y - (x - y)}{x + 2 y} \div \frac{(x + y) (x - y)}{(x + 2 y) (x + 2 y)}$ ①

$= \frac{y}{x + 2 y} \cdot \frac{(x + 2 y) (x + 2 y)}{(x + y) (x - y)}$ ②

$= \frac{y (x + 2 y)}{(x + y) (x - y)}$ ③

$= \frac{x y + 2 y^{2}}{x^{2} - y^{2}}$ ④

(1)、小明的计算步骤中，从哪一步开始出现错误？（填写序号）

(2)、小明从第①步的运算结果到第②步的运算是否正确？（填“是”或“否”）若不正确，错误的原因是．

(3)、请你帮小明写出此题完整正确的解答过程．

查看试题解析

32. 如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这个分式为“和谐分式”．

(1)、下列分式：① $\frac{x - 1}{x^{2} + 1}$ ；② $\frac{a - 2 b}{a^{2} - b^{2}}$ ；③ $\frac{x + y}{x^{2} - y^{2}}$ ；④ $\frac{a^{2} - b^{2}}{{(a + b)}^{2}}$ ．其中是“和谐分式”是　　（填写序号即可）；

(2)、若a为正整数，且 $\frac{x - 1}{x^{2} + a x + 4}$ 为“和谐分式”，请写出a的值；

(3)、在化简 $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \div \frac{b}{4}$ 时，
小东和小强分别进行了如下三步变形：

小东：原式= $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \times \frac{4}{b}$ = $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{4 a}{b^{2}}$ = $\frac{4 a^{2} b^{2} - 4 a (a b^{2} - b^{3})}{(a b^{2} - b^{3}) b^{2}}$ ，

小强：原式= $\frac{4 a^{2}}{a b^{2} - b^{3}} - \frac{a}{b} \times \frac{4}{b}$ = $\frac{4 a^{2}}{b^{2} (a - b)} - \frac{4 a}{b^{2}} = \frac{4 a^{2} - 4 a (a - b)}{(a - b) b^{2}}$ ，

显然，小强利用了其中的和谐分式，第三步所得结果比小东的结果简单，原因是：　　，

请你接着小强的方法完成化简．

查看试题解析
33. 阅读下面的解题过程：
已知 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值．
解：由已知可得 $x \neq 0$ ，则 $\frac{x^{2} + 1}{x} = 3$ ，即 $x + \frac{1}{x} = 3$ ．
$∵ \frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3^{2} - 2 = 7$ ，
$∴ \frac{x^{2}}{x^{4} + 1} = \frac{1}{7}$ ．
上面材料中的解法叫做“倒数法”．
请你利用“倒数法”解下面的题目：

(1)、已知 $\frac{x}{x^{2} - 3 x + 1} = \frac{1}{2}$ ，求 $\frac{x^{2}}{x^{4} + x^{2} + 1}$ 的值；

(2)、已知 $\frac{x y}{x + y} = 3$ ， $\frac{x z}{x + z} = \frac{4}{3}$ ， $\frac{y z}{y + z} = 1$ ，求 $\frac{x y z}{x y + x z + y z}$ 的值．

查看试题解析
34. 观察下列等式：
第1个等式： $(1 + \frac{1}{2}) \times \frac{1}{3} = 1 - \frac{1}{2}$ ，

第2个等式： $(1 + \frac{1}{3}) \times \frac{2}{4} = 1 - \frac{1}{3}$ ，

第3个等式： $(1 + \frac{1}{4}) \times \frac{3}{5} = 1 - \frac{1}{4}$ ，

第4个等式： $(1 + \frac{1}{5}) \times \frac{4}{6} = 1 - \frac{1}{5}$ ，

……

按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第 $n$ 个等式（用含 $n$ 的式子表示），并说明猜想的正确性．

查看试题解析

五、实践探究题

35. 【阅读学习】阅读下面的解题过程：
已知： $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值．
解：由 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ 知 $x \neq 0$ ，所以 $\frac{x^{2} + 1}{x} = 3$ ，即 $x + \frac{1}{x} = 3$ ，
所以 $\frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3^{2} - 2 = 7$ ，
故 $\frac{x^{2}}{x^{4} + 1}$ 的值为 $\frac{1}{7}$ ．

(1)、上题的解法叫做“倒数法”，请你利用“倒数法”解决下面的题目：
已知 $\frac{x}{x^{2} - 3 x + 1} = - 2$ ，求 $\frac{x^{2}}{x^{4} + 5 x^{2} + 1}$ 的值．

(2)、【拓展延伸】
已知 $\frac{1}{a} + \frac{1}{b} = \frac{1}{2}$ ， $\frac{1}{b} + \frac{1}{c} = \frac{1}{3}$ ， $\frac{1}{a} + \frac{1}{c} = \frac{1}{5}$ ，求 $\frac{a b c}{a b + b c + a c}$ 的值．

查看试题解析
36. 阅读材料：小明发现像 $m + n$ ， $\frac{1}{m} + \frac{1}{n}$ ， $m^{2} + n^{2}$ 等代数式，如果任意交换两个字母的位置，式子的值都不变.太神奇了！于是他把这样的式子命名为神奇对称式，他还发现像 $m^{2} + n^{2}$ ， $\frac{1}{m} + \frac{1}{n}$ 等神奇对称式都可以用 $m + n$ ， $m n$ 表示.
例如： $m^{2} + n^{2} = {(m + n)}^{2} - 2 m n$ ， $\frac{1}{m} + \frac{1}{n} = \frac{m + n}{m n}$ .

请根据以上材料解决下列问题：

(1)、① $\frac{1}{m n}$ ， ② $m^{2} - n^{2}$ ， ③ $\frac{n}{m}$ ， ④ $x y + y z + x z$ 中，是神奇对称式的有（填序号）；

(2)、已知 $(x - m) (x - n) = x^{2} - p x + q$ .
①若 $p = 3$ ， $q = 2$ ，则神奇对称式 $\frac{1}{m} + \frac{1}{n} =$ ；

②若 $q = \frac{1}{4}$ ，且神奇对称式 $m^{2} + n^{2} + \frac{1}{m} + \frac{1}{n}$ 的值为 $- \frac{1}{2}$ ，求 $p$ 的值.

查看试题解析