中考数学第一轮复习:整式(2)
试卷更新日期:2023-09-05 类型:一轮复习
一、选择题
-
1. 下列代数式:① , ② , ③5,④ , ⑤a,⑥ . 其中单项式有( )A、1个 B、2个 C、3个 D、4个2. 观察下列关于的单项式,探究其规律: , , , , , …按照上述规律,第2023个单项式是( )A、 B、 C、 D、3. 下列说法正确的是( )A、的次数是2 B、是单项式 C、是三次三项式 D、的系数是4. 若 , 下列计算正确的是( )A、 B、 C、 D、5. 下列方程的变形正确的是( )A、 , 去分母,得 B、 , 去括号,得 C、 , 移项,得 D、 , 系数化为1,得6. 下列运算正确的是( )A、 B、 C、 D、7. 关于多项式3x2-y-3xy3+x5-1,下列说法错误的是( )A、这个多项式是五次五项式 B、常数项是-1 C、四次项的系数是3 D、按x降幂排列为x5+3x2-3xy3-y-18. 有4张长为、宽为的长方形纸片,按如图的方式拼成一个边长为的正方形,图中阴影部分的面积为 , 空白部分的面积为若 , 则、满足( )
 A、 B、 C、 D、9. 计算:的结果是( )A、 B、 C、 D、10. 下列运算正确的是( )A、 B、 C、 D、11. 下列运算正确的是( )A、 B、 C、 D、12. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( )
A、 B、 C、 D、9. 计算:的结果是( )A、 B、 C、 D、10. 下列运算正确的是( )A、 B、 C、 D、11. 下列运算正确的是( )A、 B、 C、 D、12. 如图①,从边长为a的正方形中剪去一个边长为b的小正方形,然后将剩余分剪拼成一个长方形(如图②),则上述操作所能验证的公式是( ) A、 B、 C、 D、13. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如:(x- y)-(z-m-n)=x-y-z+m+n,x-y-(z-m)-n=x-y-z+m-n,……
A、 B、 C、 D、13. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简,称之为“加算操作”,例如:(x- y)-(z-m-n)=x-y-z+m+n,x-y-(z-m)-n=x-y-z+m-n,……给出下列说法:
①至少存在一种“加算操作”,使其结果与原多项式相等;②不存在任何“加算操作”,使其结果与原多项式之和为0;
对以上说法判断为( )
A、①②都正确 B、①正确,②错误 C、①错误,②正确 D、①②都错误14. 在“点燃我的梦想,数学皆有可衡”数学创新设计活动中,“智多星”小强设计了一个数学探究活动:对依次排列的两个整式m,n按如下规律进行操作:第1次操作后得到整式串m,n,;
第2次操作后得到整式串m,n, , ;
第3次操作后…
其操作规则为:每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏.
则该“回头差”游戏第2023次操作后得到的整式中各项之和是( )
A、 B、m C、 D、15. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( )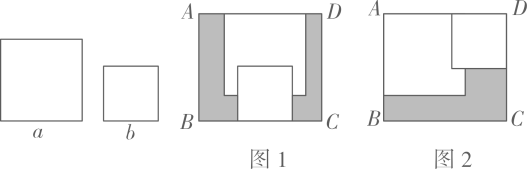 A、 B、 C、BC D、AB
A、 B、 C、BC D、AB二、填空题
-
16. 要使的展开式中不含项,则的值为 .17. F(x)表示关于x的一个五次多项式,F(a)表示x=a时F(x)的值,若F(-2)=F(-1)=F(0)=F(1)=0,F(2)=24,F(3)=360,则F(4)= .18. 表示关于的一个五次多项式,表示时的值,若 , , , 则 .19. 当时,代数式的值为 .20. 计算: .21. 若多项式可以被分解为 , 则 , , .22. ∵ , ∴ , 这说明能被整除,即或是的一个因式.另外,当即时,多项式的值为0;当即时,多项式的值为0.若能被整除,则k的值是 .23. 计算:= .24. 已知关于的多项式是一个完全平方式,则 .25. 观察下列各式的规律:;;;请将发现的规律用含的式子表示为 .
三、计算题
-
26. 化简:27. 计算:(1)、(2)、28. 计算:(1)、;(2)、 .29. 先化简,再求值: , 其中 .30. 化简: .
四、解答题
-
31. 某中学九年级的学生人数比八年级学生多.做广播操时,九年级排成的是一个规范的长方形方阵,每排人,站有排;八年级站的正方形方阵,排数和每排人数都是 , 其中 .(1)、试求该学校九年级比八年级多多少名学生;用a与b的代数式表示.(2)、当 , 时,求该学校九年级比八年级多多少名学生.32. 是否存在正整数x和y,使得 , 若存在,求出满足条件的x和y的值;若不存在,请说明理由.33. 已知实数a,b,c满足 , ,求 的值.
五、综合题
-
34. 将完全平方公式作适当变形,可以用来解决很多数学问题.
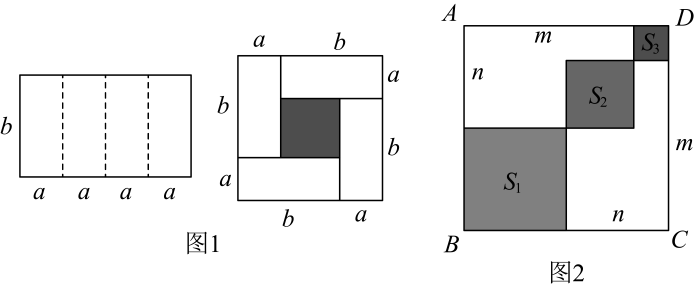 (1)、观察图1,写出代数式 , , 之间的等量关系:;(2)、若 , , 则;;(3)、如图2,边长为5的正方形中放置两个长和宽分别为m , n( , )的长方形,若长方形的周长为12,面积为 , 求图中阴影部分的面积的值.35. 对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如由图1可以得到 , 这样就用图形面积验证了完全平方公式.
(1)、观察图1,写出代数式 , , 之间的等量关系:;(2)、若 , , 则;;(3)、如图2,边长为5的正方形中放置两个长和宽分别为m , n( , )的长方形,若长方形的周长为12,面积为 , 求图中阴影部分的面积的值.35. 对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如由图1可以得到 , 这样就用图形面积验证了完全平方公式. (1)、类似地,写出图2中所表示的数学等式为;(2)、如图3,用不同的代数式表示大正方形的面积,由此得到的数学等式为;(3)、利用上面(2)的结论解决问题:若 , 求的值;(4)、利用此方法也可以求出一些不规则图形的面积.如图4,将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和 , 若这两个正方形的边长满足 , , 请求出阴影部分的面积.36. 如图,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)、类似地,写出图2中所表示的数学等式为;(2)、如图3,用不同的代数式表示大正方形的面积,由此得到的数学等式为;(3)、利用上面(2)的结论解决问题:若 , 求的值;(4)、利用此方法也可以求出一些不规则图形的面积.如图4,将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接和 , 若这两个正方形的边长满足 , , 请求出阴影部分的面积.36. 如图,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.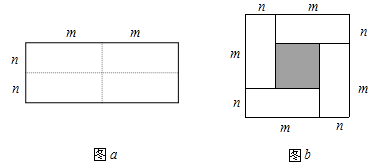 (1)、你认为图b中的阴影部分的正方形的边长等于多少?
(1)、你认为图b中的阴影部分的正方形的边长等于多少?答:
(2)、请用两种不同的方法求图b中阴影部分的面积.方法1:
方法2:
(3)、仔细观察图b,写出下列三个代数式之间的等量关系.代数式:(m+n)2 , (m-n)2 , 4mn
答:
(4)、根据(3)题中所写的等量关系,解决如下问题.若a+b=8,ab=5,则(a-b)2 = .