中考数学第一轮复习：代数式

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 某服装店新上一款运动服，第一天销售了 $m$ 件，第二天的销售量是第一天的两倍少3件，第三天比第二天多销售5件，则第三天的销售量是（）

A、 $(m + 2)$ 件 B、 $(2 m - 2)$ 件 C、 $(2 m + 2)$ 件 D、 $(2 m + 8)$ 件

查看试题解析
2. 运行程序如上图所示从“输入整数x”到“结果是否大于21”为一次程序操作，若输入整数x后程序操作仅进行了1次就停止，则x的值是（）

A、7 B、8 C、9 D、10

查看试题解析
3. 代数式 $- 2 x$ 的意义可以是（）

A、 $- 2$ 与 $x$ 的和 B、 $- 2$ 与 $x$ 的差 C、 $- 2$ 与 $x$ 的积 D、 $- 2$ 与 $x$ 的商

查看试题解析
4. 已知 $x - y = - 2$ ， $x y = 3$ ，则 $x^{2} y - x y^{2}$ 的值为（）

A、2 B、-6 C、5 D、-36

查看试题解析
5. 如果一个正整数能表示为两个连续奇数的平方差，那么称这个正整数为“幸福数”，如 $24 = 7^{2} - 5^{2}$ ， $56 = 1 5^{2} - 1 3^{2}$ ．因此24和56都是“幸福数”，则下列结论错误的是（）

A、最小的“幸福数”是8 B、520是“幸福数” C、“幸福数”一定是4的偶数倍 D、30以内的所有“幸福数”之和是49

查看试题解析
6. 如图，四边形 $O A B C_{1}$ 是正方形，曲线 $C_{1} C_{2} C_{3} C_{4} C_{5} ⋯$ 叫作“正方形的渐开线”，其中 $\overset{⌢}{C_{1} C_{2}}$ ， $\overset{⌢}{C_{2} C_{3}}$ ， $\overset{⌢}{C_{3} C_{4}}$ ， $\overset{⌢}{C_{4} C_{5}}$ ， …的圆心依次按O ， A ， B， $C_{1}$ 循环．当 $O A = 1$ 时，点 $C_{2023}$ 的坐标是（）

A、 $(- 1 ， - 2022)$ B、 $(- 2023 ， 1)$ C、 $(- 1 ， - 2023)$ D、 $(2022 ， 0)$

查看试题解析
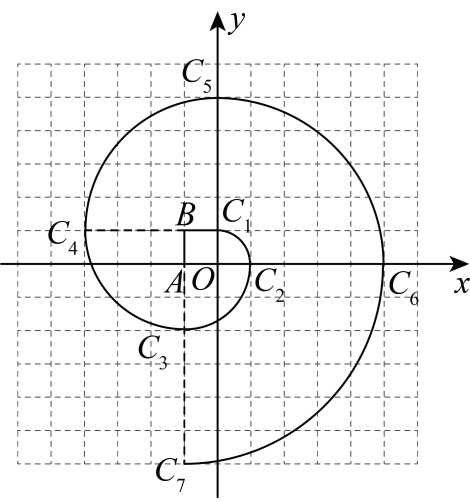7. 在平面直角坐标系中，对于点 $A (x ， y)$ ，若点 $A^{'}$ 坐标为 $(a x + y ， x + a y)$ （其中a常数，且 $a \neq 0$ ），则称点 $A^{'}$ 是点A的“a属派生点”．例如，点 $P (4 ， 3)$ 的“2属派生点”为 $P^{'} (2 \times 4 + 3 ， 4 + 2 \times 3)$ ，即 $P^{'} (11 ， 10)$ ．若点Q的“3属派生点”是点 $Q^{'} (- 7 ， - 5)$ ，则点Q的坐标为（）

A、 $(- 26 ， - 22)$ B、 $(- 22 ， - 26)$ C、 $(- 2 ， - 1)$ D、 $(- 1 ， - 2)$

查看试题解析
8. 一列单项式按以下规律排列： $x$ ， $- 3 x^{2}$ ， $5 x^{2}$ ， $- 7 x$ ， $9 x^{2}$ ， $- 11 x^{2}$ ， $13 x$ ， $⋯$ ，则第 $2023$ 个单项式是（）

A、 $4045 x$ B、 $- 4045 x^{2}$ C、 $4045 x^{2}$ D、 $- 4045 x$

查看试题解析
9. 如图，在平面直角坐标系中，一动点从原点 $O$ 出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点 $A_{1} (0 ， 1)$ ， $A_{2} (1 ， 1)$ ， $A_{3} (1 ， 0)$ ， $A_{4} (2 ， 0)$ ， …那么点 $A_{2023}$ 的坐标为（）

A、 $A_{2023} (1011 ， 1)$ B、 $A_{2023} (1 ， 1011)$ C、 $A_{2023} (1011 ， 0)$ D、 $A_{2023} (0 ， 1011)$

查看试题解析
10. 如图在平面直角坐标系 $x O y$ 中，有一个等腰直角三角形 $A O B$ ， $∠ O A B = 90 °$ ，直角边 $A O$ 在x轴上，且 $A O = 1$ ．将 $R t △ A O B$ 绕原点O顺时针旋转 $90 °$ 得到等腰直角三角形 $A_{1} O B_{1}$ ，且 $A_{1} O = 2 A O$ ，再将 $R t △ A_{1} O B_{1}$ 绕原点O顺时针旋转90°得到等腰三角形 $A_{2} O B_{2}$ ，且 $A_{2} O = 2 A_{1} O$ ……，依此规律，得到等腰直角三角形 $A_{2023} O B_{2023}$ ．则点 $B_{2023}$ 的坐标（）

A、 $(- 2^{2023} ， 2^{2023})$ B、 $(2^{2022} ， - 2^{2022})$ C、 $(2^{2023} ， - 2^{2023})$ D、 $(2^{2022} ， 2^{2022})$

查看试题解析

二、填空题

11. 周末小希跟几位同学在某快餐厅吃饭，如下为此快餐厅的菜单．若他们所点的餐食总共为8份盖饭，x杯饮料，y份凉拌菜．
A套餐：一份盖饭加一杯饮料
B套餐：一份盖饭加一份凉拌菜
C套餐：一份盖饭加一杯饮料与一份凉拌菜

(1)、他们点了份B套餐（用含x或y的代数式表示，其中 $x \neq 0 ， y \neq 0$ ）；

(2)、如果 $x = 5$ ，且A、B、C套餐均至少点了1份，那么最多有种点餐方案．

查看试题解析

12. 如图是某种杆秤．在秤杆的点

A

处固定提纽，点

B

处挂秤盘，点

C

为0刻度点．当秤盘不放物品时，提起提纽，秤砣所挂位置移动到点

C

，秤杆处于平衡．秤盘放入

x

克物品后移动秤砣，当秤砣所挂位置与提扭的距离为

y

毫米时秤杆处于平衡．测得

x

与

y

的几组对应数据如下表：

$x$ /克	0	2	4	6	10
$y$ /毫米	10	14	18	22	30

由表中数据的规律可知，当 $x = 20$ 克时， $y =$ 毫米．

查看试题解析

13. 2023长春马拉松于5月21日在南岭体育场鸣枪开跑，某同学参加了7.5公里健康跑项目，他从起点开始以平均每分钟x公里的速度跑了10分钟，此时他离健康跑终点的路程为公里．（用含x的代数式表示）

查看试题解析
14. 若 $x = \sqrt{5} - 3$ ，则 $\sqrt{x^{2} + 6 x + 9}$ 的值为.

查看试题解析
15. 1261年，我国宋朝数学家杨辉在其著作《详解九章算法》中提到了如图所示的数表，人们将这个数表称为“杨辉三角”．

观察“杨辉三角”与右侧的等式图，根据图中各式的规律， $(a + b)^{7}$ 展开的多项式中各项系数之和为．

查看试题解析
16. 在平面直角坐标系中，一个智能机器人接到的指令是：从原点 $O$ 出发，按“向上→向右→向下→向右→向下→向右→向上→向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示．第一次移动到点 $A_{1}$ ，第二次移动到点 $A_{2}$ ， …，第 $n$ 次移动到点 $A_{n}$ ，则点 $A_{2024}$ 的坐标是．

查看试题解析
17. 如图，第1个图中有1个三角形，第2个图中共有5个三角形，第3个图中共有9个三角形，…，依此类推，则第2023个图中共有个三角形．

查看试题解析
18. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ ，我们把 $P^{'} (- y + 1 ， x + 1)$ 叫做点 P的伴随点，已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ … ，这样依次得到点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， … ， $A_{n}$ …若点 $A_{1}$ 的坐标为 $(4 ， 3)$ ，则点 $A_{2023}$ 的坐标为．

查看试题解析
19. 如图，在平面直角坐标系中，四边形 $A_{1} B_{1} B_{2} C_{1}$ ， $A_{2} B_{2} B_{3} C_{2}$ ， $A_{3} B_{3} B_{4} C_{3}$ ， $A_{4} B_{4} B_{5} C_{4}$ ， …都是平行四边形，顶点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， $B_{4}$ ， $B_{5}$ ， …都在 $x$ 轴上，顶点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， $C_{4}$ ， …都在正比例函数 $y = \frac{1}{4} x$ （ $x \geq 0$ ）的图象上，且 $B_{2} C_{1} = 2 A_{2} C_{1}$ ， $B_{3} C_{2} = 2 A_{3} C_{2}$ ， $B_{4} C_{3} = 2 A_{4} C_{3}$ ， …，连接 $A_{1} B_{2}$ ， $A_{2} B_{3}$ ， $A_{3} B_{4}$ ， $A_{4} B_{5}$ ， …，分别交射线 $O C_{1}$ 于点 $O_{1}$ ， $O_{2}$ ， $O_{3}$ ， $O_{4}$ ， …，连接 $O_{1} A_{2}$ ， $O_{2} A_{3}$ ， $O_{3} A_{4}$ ， …，得到 $Δ O_{1} A_{2} B_{2}$ ， $Δ O_{2} A_{3} B_{3}$ ， $Δ O_{3} A_{4} B_{4}$ ， …．若 $B_{1} (2 ， 0)$ ， $B_{2} (3 ， 0)$ ， $A_{1} (3 ， 1)$ ，则 $Δ O_{2023} A_{2024} B_{2024}$ 的面积为．

查看试题解析
20. 如图，在单位为1的方格纸上， $△ A A_{1} A_{2}$ ， $△ A_{2} A_{3} A_{4}$ ， $△ A_{4} A_{5} A_{6}$ ， …，都是斜边在x轴上，斜边长分别为2，4，6，8，10，…的等腰直角三角形，若 $△ A A_{1} A_{2}$ 的顶点坐标分别为 $A (1 ， 0)$ ， $A_{1} (0 ， 1)$ ， $A_{2} (- 1 ， 0)$ ．则依图中所示规律， $A_{2024}$ 的坐标为．

查看试题解析
21. 如图，在边长为 $a$ 的等边 $△ A B C$ 中，分别取 $△ A B C$ 三边的中点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，得 $△ A_{1} B_{1} C_{1}$ ；再分别取 $△ A_{1} B_{1} C_{1}$ 三边的中点 $A_{2}$ ， $B_{2}$ ， $C_{2}$ ，得 $△ A_{2} B_{2} C_{2}$ ；这样依次下去 $\dots$ ，经过第 $2022$ 次操作后得 $△ A_{2023} B_{2023} C_{2023}$ ，则 $△ A_{2023} B_{2023} C_{2023}$ 的面积为．

查看试题解析
22. 如图，在平面直角坐标系中，函数 $y = 2 x$ 和 $y = - x$ 的图象分别为直线 $l_{1}$ 和 $l_{2}$ ，过点 $(1 ， 0)$ 作 $x$ 轴的垂线交 $l_{1}$ 于点 $A_{1}$ ，过点 $A_{1}$ 作y轴的垂线交 $l_{2}$ 于点 $A_{2}$ ，过点 $A_{2}$ 作x轴的垂线交 $l_{1}$ 于点 $A_{3}$ ，过点 $A_{3}$ 作y轴的垂线交 $l_{2}$ 于点 $A_{4}$ ， …依次进行下去，则点 $A_{2023}$ 的坐标为．

查看试题解析

三、计算题

23. 已知 $y = \sqrt{x - 3} + \sqrt{3 - x} + 4$ ，求 ${(x - y)}^{2023}$ 的值．

查看试题解析

四、解答题

24. 某地粮库需要把晾晒场上的120吨小麦入库封存，受设备影响，平均每天入库15吨，入库所用的时间为x(单位：天)，未入库小麦的质量为y(单位：吨)

(1)、写出未入库小麦的质量y与入库所用的时间x之间的关系式；

(2)、当 $x = 6$ 时，未入库小麦的质量有多少吨?

(3)、当x为多少时，未入库小麦的质量为45吨?

查看试题解析
25. 一个正方体的棱长是x ，体积是1．一个正方形的边长是y ，面积是16，求 $\sqrt{4 x + 3 y}$ 的值．

查看试题解析
26. 观察下列等式，然后用你发现的规律解答下列问题．
第1个等式 $1 - \frac{1}{3} = \frac{2}{1 \times 3}$
第2个等式 $\frac{1}{2} - \frac{1}{4} = \frac{2}{2 \times 4}$
第3个等式 $\frac{1}{3} - \frac{1}{5} = \frac{2}{3 \times 5}$
第4个等式 $\frac{1}{4} - \frac{1}{6} = \frac{2}{4 \times 6}$
……

(1)、请写出第7个等式；

(2)、请写出第 $n$ 个等式；

(3)、计算 $\frac{1}{1 \times 3} + \frac{1}{2 \times 4} + \frac{1}{3 \times 5} + \dots + \frac{1}{8 \times 10}$ ．

查看试题解析
27. 定义新运算：对于任意实数a和b ，都有 $a ※ b = a b - 2 a + b - 3$ ，例如 $1 ※ 4 = 1 \times 4 - 2 \times 1 + 4 - 3 = 3$ ．若 $3 ※ x$ 的值是非负数，求x的取值范围．

查看试题解析

五、实践探究题

28. 观察下列各式，回答问题：
① $\sqrt{2 \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ ；② $\sqrt{3 \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ ；③ $\sqrt{4 \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$ ．

(1)、上述式子中，正确的是；

(2)、类比上述式子，可得第④个式子是；

(3)、从（1），（2）的结论中，你能看出其中的规律吗？用字母表示这一规律，并给出证明．

查看试题解析
29. 定义一种新运算 $x \otimes y = a x + y$ ．

(1)、若 $a = 2$ ，求满足 ${\begin{cases} （ x - 1) \otimes y = 7 \\ x \otimes (- 3 y) = 1 \end{cases}$ 的x、y的解；

(2)、若关于 $x$ 的不等式 $x \otimes 1 > 0$ 的解集为x＜3，求 $a$ 的值．

查看试题解析

六、综合题

30. 小明爸爸想锻炼小明的独立生活能力并提高用数学知识解决实际问题的能力，让小明周末期间去姑姑家，到姑姑家后，下面是一段对话：
小明：坐出租车价格怎么计费？

姑姑：2公里以内6元，还要加1元的燃油补贴，超过2公里，超出部分每公里2元，超出部分不再出燃油补贴，但不足1公里按1公里计费，例如 $3.1$ 公里按4公里收费．

根据对话解答下列问题：

(1)、小明乘出租车去 $2.6$ 公里处的风景点A处要付司机元．

(2)、小明乘出租车去x公里( $x > 2$ 且x为整数)的风景点B处，要付钱元（用含x的代数式表示）

(3)、小明从风景点B处去C处，下了出租车交给司机师傅13元，说：“师傅，这些钱够不够？”师傅说：“钱数恰好，且路程也刚好为整数．”小明回家后告诉爸爸，我知道从风景点B到风景点C处有多少公里了．请你帮小明算一算．

查看试题解析
31. 有 $7$ 个如图 $1$ 的边长分别为 $a$ ， $b$ 的小长方形，拼成如图 $2$ 的大长方形．

(1)、观察图 $2$ ，请你写出 $a$ ， $b$ 满足的等量关系（用含 $a$ 的代数式表示 $b$ ）；

(2)、将这 $7$ 个图 $1$ 的小长方形放入一个大长方形中，摆放方式如图 $3$ 所示（小长方形都呈水平或竖直摆放），图中的阴影部分分别记为Ⅰ、Ⅱ、Ⅲ．
$①$ 记阴影部分Ⅰ、Ⅱ的周长分别为 $m_{1}$ ， $m_{2}$ ，试求 $\frac{m_{1}}{m_{2}}$ 的值；

$②$ 若阴影部分Ⅰ、Ⅱ、Ⅲ的面积之和为 $86$ ，求 $a$ ， $b$ 的值．

查看试题解析

32. 阅读下列材料，完成相应的任务：

三角形数

古希腊著名数学家的毕达哥拉斯学派把1，3，6，10，．．．，这样的数称为“三角形数”，第n个“三角形数”可表示为： $1 + 2 + 3 + \cdot \cdot \cdot + n = \frac{n (n + 1)}{2}$ ．

发现：每相邻两个“三角形数”的和有一定的规律．如： $1 + 3 = 4$ ； $3 + 6 = 9$ ； $6 + 10 = 16$ ；…

(1)、第5个“三角形数”与第6个“三角形数”的和为；

(2)、第n个“三角形数”与第

(n + 1)

个“三角形数”的和的规律可用下面等式表示：+= ，请补全等式并说明它的正确性．

查看试题解析

33. 通过一次数学活动我们发现，如果两个两位数的十位数字相同，个位数字的和为10，那么这样的两位数相乘会有如下规律：
      $24 \times 26 = (2 \times 3) \times 100 + 4 \times 6 = 624$

      $52 \times 58 = (5 \times 6) \times 100 + 2 \times 8 = 3016$

      $84 \times 86 = (8 \times 9) \times 100 + 4 \times 6 = 7224$

这组计算蕴含着简算规律：十位数字相同，个位数字和为10的两个两位数相乘，积的末两位数是个位数字的乘积，前几位是十位数字与十位数字加一的乘积．

(1)、若有两个两位数的十位数字相同，个位数字的和为10的两个数的乘积为4221，请你利用小组发现的规律写出这两个数×；

(2)、若设这两个两位数相同的十位数字为a，个位数字分别设为b、d，请你用学过的知识证明十位数字相同，个位数字的和为10的这样的两位数的乘积的一般规律．
证明： $\bar{a b} \cdot \bar{a d} = (10 a + b) (10 a + d)$

      $= 100 a^{2} + 10 a b + 10 a d + b d$

      $= 100 a^{2} +_____+ b d$

      $∵ b + d =$ ，

      $∴ \bar{a b} \cdot \bar{a d} =$

查看试题解析
34. 定义一种幂的新运算： $x^{a} \oplus x^{b} = x^{a b} + x^{a + b}$ ，请利用这种运算规则解决下列问题：

(1)、求 $2^{2} \oplus 2^{3}$ 的值；

(2)、若 $2^{p} = 3$ ， $2^{q} = 5$ ， $3^{q} = 6$ ，求 $2^{p} \oplus 2^{q}$ 的值；

(3)、若运算 $9 \oplus 3^{2 t}$ 的结果为810，则t的值是多少？

查看试题解析