中考数学第一轮复习：有理数

试卷更新日期：2023-09-05 类型：一轮复习

进入出卷网下载

一、选择题

1. 负数的概念最早出现在我国古代著名的数学专著《九章算术》中，如果把收入5元记作+5元，那么支出5元记作（）

A、 $- 5$ 元 B、0元 C、 $+ 5$ 元 D、 $+ 10$ 元

查看试题解析
2. 在实数 $\sqrt[3]{8}$ ， $\sqrt{3}$ ， $\frac{4}{3}$ 中，有理数有（　　）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 如图，数轴上A、B两点到原点的距离是三角形两边的长，则该三角形第三边长可能是（）

A、1 B、4 C、7 D、8

查看试题解析
4. 下面各数中最小的是（）

A、 $2023^{0}$ B、 $- 2023$ C、 ${(\frac{1}{2023})}^{- 1}$ D、 $- \frac{1}{2023}$

查看试题解析
5. $- 2023$ 的相反数是（）

A、 $- 2023$ B、2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
6. $- \frac{1}{10}$ 的绝对值是（）

A、 $\frac{1}{10}$ B、10 C、 $- \frac{1}{10}$ D、 $- 10$

查看试题解析
7. 在下列计算中，正确的是（）

A、 $5 + (- 6) = - 1$ B、 $\frac{1}{\sqrt{2}} = \sqrt{2}$ C、 $3 \times (- 2) = 6$ D、 $s i n 30 ° = \frac{\sqrt{3}}{3}$

查看试题解析
8. 计算： $2 - (- 3)$ 的结果是（　　）

A、5 B、1 C、-1 D、-5

查看试题解析
9. $\sqrt{2}$ 的倒数是（　　）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{2}}{2}$ D、 $- \frac{\sqrt{2}}{2}$

查看试题解析
10. 计算 $3 \div (- \frac{1}{3})$ 的结果等于（　　）

A、 $- 9$ B、9 C、 $- 1$ D、1

查看试题解析
11. 下列运算正确的是（）

A、 ${(- a)}^{3} = a^{3}$ B、 ${(x - y)}^{2} = x^{2} - y^{2}$ C、 ${(a^{2})}^{3} = a^{3}$ D、 $(b + a) (b - a) = b^{2} - a^{2}$

查看试题解析
12. 下列运算结果正确的是（）

A、 $(x + 3)^{2} = x^{2} + 9$ B、 $x^{12} \div x^{6} = x^{6}$ C、 $2 x + 3 y = 5 x y$ D、 $x^{12} - x^{6} = x^{6}$

查看试题解析
13. 下列近似数，精确到 $0.001$ 且有三个有效数字的是（）

A、 $8.010$ B、 $8.01$ C、 $0.801$ D、 $0.081$

查看试题解析
14. 下列说法正确的是（）

A、 $\frac{\sqrt{2}}{2}$ 是分数 B、16的平方根是±4，即 $\sqrt{16} = \pm 4$ C、8.30万精确到百分位 D、若 $\sqrt{a - 2022} + | b + 1 | = 0$ ，则 $b^{a} = 1$

查看试题解析

二、填空题

15. 在数1，2，3，…，2022前添加“＋”“－”并依次计算，所得的结果中最小的非负数是．

查看试题解析
16. 已知二次三项式 $x^{2} + b x + c$ 可以因式分解为 $(x - 1) (x - 5)$ ，则 $b + c$ 的值为．

查看试题解析
17. 如图，利用课本上的计算器进行计算，其按键顺序及结果如下：

①按键的结果为4；
②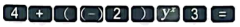按键的结果为8；
③按键的结果为 $0.5$ ；
④按键的结果为25．
以上说法正确的序号是．

查看试题解析
18. 船闸是我国劳动人民智慧的结晶，三峡船闸的“人”字闸门是目前世界上最大的巨型闸门，重867000千克，用科学记数法表示为千克．

查看试题解析
19. 10位裁判给一位运动员打分,每个人给的分数都是整数,去掉一个最高分,再去掉一个最低分,其余得分的平均数为该运动员的得分。若用四舍五入取近似值的方法精确到十分位,该运动员得9.4分,如果精确到百分位,该运动员得分应当是分.

查看试题解析
20. 2023年3月12日是我国第45个植树节，某林业部门为了考察某种幼树在一定条件下的移植成活率，在同等条件下，对这种幼树进行大量移植，并统计成活情况，下表是这种幼树移植过程中的一组统计数据：
幼树移植数（棵）
100
1000
5000
8000
10000
15000
20000
幼树移植成活数（棵）
87
883
4455
7209
8983
13519
18044
幼树移植成活的频率
0.8700
0.8820
0.8910
0.9011
0.8983
0.9013
0.9022
估计该种幼树在此条件下移植成活率是.（结果精确到 $1 %$ ）

查看试题解析
21. 用四舍五入法把3.1415926精确到0.01，所得到的近似数为．

查看试题解析

三、计算题

22. 计算

(1)、 $(\frac{1}{4} + \frac{1}{6} - \frac{1}{2}) \times 12$

(2)、 $- 7^{2} + 2 \times {(- 3)}^{2} - (- 6) \div {(- \frac{1}{3})}^{2}$

查看试题解析
23.

(1)、计算： ${(- 2)}^{2} - {(2023 - 2022)}^{0} - {(- \frac{1}{2})}^{- 2}$ ；

(2)、计算： $[{(x + y)}^{2} - {(x - y)}^{2}] \div 2 x y$ ．

查看试题解析
24. 计算： $- 1^{3} - \frac{1}{4} \times [1 - {(- 5)}^{2}] + \sqrt[3]{- 27}$

查看试题解析
25. 利用乘法公式计算：

(1)、 $32 5^{2} - 27 5^{2}$ ；

(2)、 $295 \times 305 - 29 8^{2}$ ．

查看试题解析
26. 用计算器计算，结果保留三位小数：

(1)、 $5^{\frac{1}{3}}$ ；

(2)、 ${(\frac{5}{7})}^{\frac{3}{4}}$ ；

(3)、 $1 0^{\frac{2}{3}}$ ．

查看试题解析

四、解答题

27. 某中学积极倡导阳光体育运动，提高中学生身体素质，开展跳绳比赛，下表为该校（1）班42人参加跳绳比赛的情况，若标准数量为每人每分钟100个．
跳绳个数与标准数量的差值
$- 2$
$- 1$
0
4
5
6
人数
6
12
2
7
10
5
求八（1）班42人一分钟内平均每人跳绳多少个？

查看试题解析
28. 观察：1+2=3=2²-1，1+2+2²=7=2³-1，1+2+2²+2³=15=2⁴-1，….又2³²约为4.3×10⁹ ，则1+2+2²+2³+…+2³¹约为多少?用科学记数法表示为a×10ⁿ的形式，并判断它是几位数.(a的值精确到0.1)

查看试题解析
29. 一个篮球的体积为 $9850 c m^{3}$ ，求该篮球的半径 $r$ （ $π$ 取 $3.14$ ，结果精确到 $0.1 c m$ ）.

查看试题解析
30. 在做浮力实验时，小亮用一根细线将一正方体铁块拴住，完全浸入盛满水的烧杯中，并用一量筒量得被铁块排开的水的体积为 $40.5 c m^{3}$ ，小亮又将铁块从水中提起，量得烧杯中的水位下降了 $0.62 c m$ .求：烧杯内部的底面半径和铁块的棱长各是多少？（用计算器计算，结果精确到 $0.1 c m$ ，排开水的体积与铁块的体积相等）

查看试题解析

五、实践探究题

31. “我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法，配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等问题．例如：

分解因式： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 3 - 1 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ．

求代数式 $2 x^{2} + 4 x - 6$ 的最小值： $2 x^{2} + 4 x - 6 = 2 (x^{2} + 2 x) - 6 = 2 (x^{2} + 2 x + 1) - 6 - 2 = 2 {(x + 1)}^{2} - 8$ ．

∵ ${(x + 1)}^{2} \geq 0$ ， ∴ $2 {(x + 1)}^{2} - 8 \geq - 8$ ， ∴当 $x = - 1$ 时， $2 x^{2} + 4 x - 6$ 有最小值，最小值是 $- 8$ ．

根据材料用配方法解决下列问题：

(1)、分解因式： $x^{2} - 4 x - 5$ ；

(2)、当 $x$ 为何值时，多项式 $- 2 x^{2} - 4 x + 3$ 有最大值？并求出这个最大值．

查看试题解析
32. 阅读材料，完成下列任务：
材料1：因为无理数是无限不循环小数，所以无理数的小数部分我们不可能全部写出来．比如： $π$ ， $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确．
材料2：2.5的整数部分是2，小数部分是0.5，小数部分可以看成是 $2.5 - 2$ 得来的．
材料3：任何一个无理数，都夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ．
根据上述材料，回答下列问题：（参考值： $\sqrt{3} \approx 1.732$ ）

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $5 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 5 + \sqrt{3} < b$ ，求 $a + b$ 的值．

(3)、已知 $3 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x + 4 y$ 的近似值（精确到0.1）．

查看试题解析

六、综合题

33. 如图，在平面直角坐标系中，已知 $A (a ， 0)$ ， $B (b ， 0)$ ，其中a ， b满足 $\sqrt{a + 1} + {(b - 3)}^{2} = 0$ ，

(1)、填空： $a =$ ， $b =$ ．

(2)、若在第三象限内有一点 $M (- 2 ， m)$ ，用含m的式子表示 $△ A B M$ 面积．

(3)、在（2）条件下，当 $m = - \frac{3}{2}$ 时，线段 $B M$ 与y轴相交于 $C (0 ， - \frac{9}{10})$ ，点P是坐标轴上的动点，当满足 $△ P B M$ 面积是 $△ A B M$ 面积的2倍时，直接写出点P的坐标．

查看试题解析
34. 观察下列式子：
第1个式子： $f (1) = \frac{1}{2^{2}} < \frac{1}{1 \times 2} = \frac{1}{1} - \frac{1}{2}$ ；
第2个式子： $f (2) = \frac{1}{3^{2}} < \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ；
第3个式子： $f (3) = \frac{1}{4^{2}} < \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ；
第4个式子： $f (4) = \frac{1}{5^{2}} < \frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ；
……
根据上述规律，解决下列问题：

(1)、写出第5个式子：；

(2)、写出第 $n$ （ $n$ 为正整数）个式子，并说明： $f (1) + f (2) + f (3) + \cdot \cdot \cdot + f (n) < 1$ ．

查看试题解析
35. 阅读理解：已知 $x \neq y$ ， $p = x^{2} - y^{2}$ ， $q = 2 x y - 2 y^{2} .$ 试比较 $p$ 与 $q$ 的大小．
想法：求 $p - q .$ 当 $p - q > 0$ ，则 $p > q$ ；当 $p - q < 0$ ，则 $p < q$ ；当 $p - q = 0$ ，则 $p = q$ ．
解： $∵ p - q = (x^{2} - y^{2}) - (2 x y - 2 y^{2}) = x^{2} - 2 x y + y^{2} = (x - y)^{2} > 0$ ， $∴ p > q$ ．
用你学到的方法解决下列问题：

(1)、已知 $- 1 < x < 1$ 且 $x \neq 0$ ， $m = \frac{x}{1 + x}$ ， $n = \frac{x}{1 - x} .$ 试比较 $m$ 与 $n$ 的大小．

(2)、甲、乙两地相距 $s (k m)$ ，小明和小宇同路往返于甲乙两地．小明去时和返回时的速度分别是 $a (k m / h)$ 、 $b (k m / h)$ ， $a \neq b$ ；小宇去时和返回时的速度都是 $\frac{a + b}{2} (k m / h) .$ 请问二者一个来回中，谁用时更短？

查看试题解析
36. 对非负实数x“四舍五入”到个位的值记作<x>，即：当n为非负整数时，若n－ $\frac{1}{2}$ ≤x＜n＋ $\frac{1}{2}$ ，则<x>=n.如：<0>=<0.48>=0，<0.64>=<1.493>=1，<2>=2，<3.5>=<4.12>=4，….

(1)、填空：
①<π>=；

②如果<2x－1>=3，则实数x的取值范围为；

(2)、举例说明<x＋y>＝<x>＋<y>不恒成立；

(3)、求满足<x>= $\frac{4}{3}$ x的所有非负实数x的值.

查看试题解析

幼树移植数（棵）	100	1000	5000	8000	10000	15000	20000
幼树移植成活数（棵）	87	883	4455	7209	8983	13519	18044
幼树移植成活的频率	0.8700	0.8820	0.8910	0.9011	0.8983	0.9013	0.9022

跳绳个数与标准数量的差值	$- 2$	$- 1$	0	4	5	6
人数	6	12	2	7	10	5