2023年黑龙江省中考数学真题分类汇编9 锐角三角函数与三视图
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 七个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
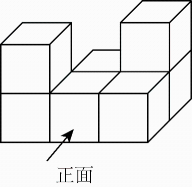 A、
A、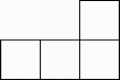 B、
B、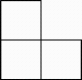 C、
C、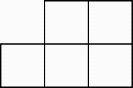 D、
D、 2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )
2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )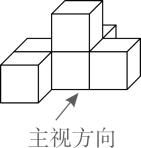 A、2 B、3 C、4 D、53. 一个长方体被截去一部分后,得到的几何体如图水平放置,其俯视图是( )
A、2 B、3 C、4 D、53. 一个长方体被截去一部分后,得到的几何体如图水平放置,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
4. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )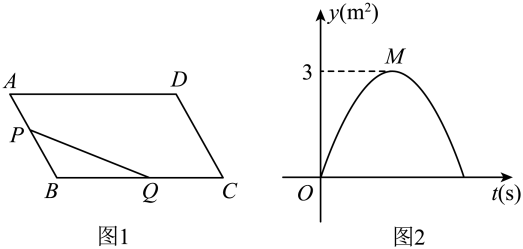 A、 B、 C、 D、5. 由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最多是( )
A、 B、 C、 D、5. 由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最多是( )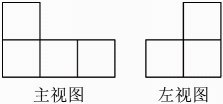 A、6 B、7 C、8 D、96. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( )
A、6 B、7 C、8 D、96. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( ) A、 B、 C、 D、7. 如图是一个正方体,被切去一角,则其左视图是( )
A、 B、 C、 D、7. 如图是一个正方体,被切去一角,则其左视图是( )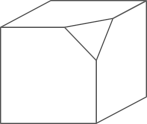 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
8. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤9. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤9. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
① ② ③当时,
A、0个 B、1个 C、2个 D、3个二、填空题
-
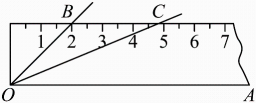
10. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .
 11. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .
11. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .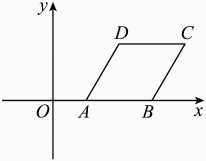 12. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是.
12. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是.
三、计算题
-
13. 先化简,再求代数式的值,其中 .14. 计算: .15. 先化简,再求值: , 其中 .16. 先化简,再求值: , 其中 .17.(1)、计算:(2)、分解因式:
四、作图题
-
18. 在中, , , , D为的中点,以为直角边作含角的 , , 且点E与点A在的同侧,请用尺规或三角板作出符合条件的图形,并直接写出线段的长.
五、解答题
-
19. 某风景区观景缆车路线如图所示,缆车从点出发,途经点后到达山顶 , 其中米,米,且段的运行路线与水平方向的夹角为 , 段的运行路线与水平方向的夹角为 , 求垂直高度 . (结果精确到米,参考数据: , , )

六、综合题
-
20. 如图,是的直径,点是圆上的一点,于点 , 交于点 , 连接 , 若平分 , 过点作于点 , 交于点 , 延长 , 交于点 .
 (1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.21. 如图,在中, , AD平分交BC于点D,点E是斜边AC上一点,以AE为直径的经过点D,交AB于点F,连接DF.
(1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.21. 如图,在中, , AD平分交BC于点D,点E是斜边AC上一点,以AE为直径的经过点D,交AB于点F,连接DF. (1)、求证:BC是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 如图,直线和为河的两岸,且 , 为了测量河两岸之间的距离,某同学在河岸的B点测得 , 从B点沿河岸的方向走40米到达D点,测得.
(1)、求证:BC是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).22. 如图,直线和为河的两岸,且 , 为了测量河两岸之间的距离,某同学在河岸的B点测得 , 从B点沿河岸的方向走40米到达D点,测得.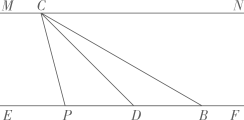 (1)、求河两岸之间的距离是多少米?(结果保留根号)(2)、若从D点继续沿的方向走米到达P点.求的值.23. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表:
(1)、求河两岸之间的距离是多少米?(结果保留根号)(2)、若从D点继续沿的方向走米到达P点.求的值.23. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表: (1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.24. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题:
(1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.24. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题: (1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.
(1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.25. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.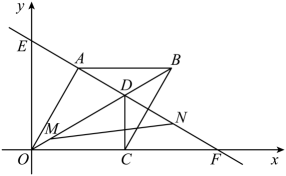 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.26. 如图,为的直径,且 , 与为圆内的一组平行弦,弦交于点H.点A在上,点B在上,.
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.26. 如图,为的直径,且 , 与为圆内的一组平行弦,弦交于点H.点A在上,点B在上,. (1)、求证:.(2)、求证:.(3)、在中,沿弦所在的直线作劣弧的轴对称图形,使其交直径于点G.若 , 求的长.
(1)、求证:.(2)、求证:.(3)、在中,沿弦所在的直线作劣弧的轴对称图形,使其交直径于点G.若 , 求的长.
-
-