2023年黑龙江省中考数学真题分类汇编8 相似
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 七个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
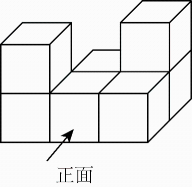 A、
A、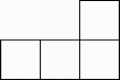 B、
B、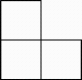 C、
C、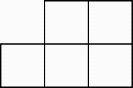 D、
D、 2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )
2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )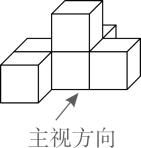 A、2 B、3 C、4 D、53. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( )
A、2 B、3 C、4 D、53. 如图, , 相交于点 , , 是的中点, , 交于点 . 若 , 则的长为( ) A、2 B、4 C、6 D、84. 一个长方体被截去一部分后,得到的几何体如图水平放置,其俯视图是( )
A、2 B、4 C、6 D、84. 一个长方体被截去一部分后,得到的几何体如图水平放置,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最多是( )
5. 由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最多是( )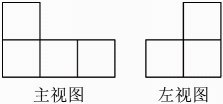 A、6 B、7 C、8 D、96. 如图是一个正方体,被切去一角,则其左视图是( )
A、6 B、7 C、8 D、96. 如图是一个正方体,被切去一角,则其左视图是( )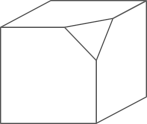 A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
① ② ③当时,
A、0个 B、1个 C、2个 D、3个9. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( ) A、
A、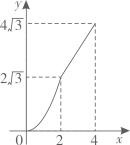 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片如图所示,点在边上,现将矩形折叠,折痕为 , 点对应的点记为点 , 若点恰好落在边上,则图中与一定相似的三角形是 .
 11. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)
11. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)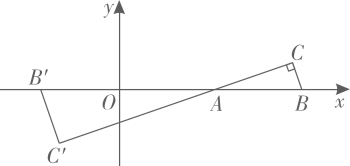 12. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 .
12. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 . 13. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
13. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
三、解答题
-
14. 如图①,和是等边三角形,连接 , 点F,G,H分别是和的中点,连接 . 易证: .
若和都是等腰直角三角形,且 , 如图②:若和都是等腰三角形,且 , 如图③:其他条件不变,判断和之间的数量关系,写出你的猜想,并利用图②或图③进行证明.

四、综合题
-
15. 如图,是的直径,点是圆上的一点,于点 , 交于点 , 连接 , 若平分 , 过点作于点 , 交于点 , 延长 , 交于点 .
 (1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.16. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题:
(1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.16. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题: (1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
(1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.
-

