2023年黑龙江省中考数学真题分类汇编6 圆
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 如图,是的切线,A为切点,连接﹐点C在上, , 连接并延长,交于点D , 连接 . 若 , 则的度数为( )
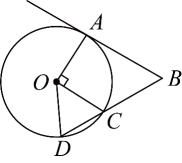 A、 B、 C、 D、2. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )
A、 B、 C、 D、2. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )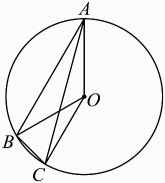 A、 B、 C、 D、12°3. 用一个圆心角为 , 半径为8的扇形作一个圆锥的侧面,则这个圆锥的底面直径是( )A、6 B、5 C、4 D、3
A、 B、 C、 D、12°3. 用一个圆心角为 , 半径为8的扇形作一个圆锥的侧面,则这个圆锥的底面直径是( )A、6 B、5 C、4 D、3二、填空题
-
4. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.5. 如图,是的直径,切于点A,交于点 , 连接 , 若 , 则 .
 6. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .7. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .8. 如图,的半径为2 , 为的弦,点C为上的一点,将沿弦翻折,使点C与圆心O重合,则阴影部分的面积为.(结果保留π与根号)
6. 已知圆锥的母线长 , 侧面积 , 则这个圆锥的高是 .7. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .8. 如图,的半径为2 , 为的弦,点C为上的一点,将沿弦翻折,使点C与圆心O重合,则阴影部分的面积为.(结果保留π与根号)
三、作图题
-
9. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , .
 (1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).10. 已知:点P是外一点.
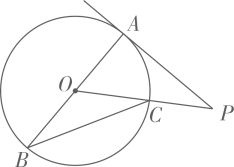
(1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).10. 已知:点P是外一点. (1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.
(1)、尺规作图:如图,过点P作出的两条切线 , , 切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.四、解答题
-
11. 已知内接于 , 为的直径,N为的中点,连接交于点H .
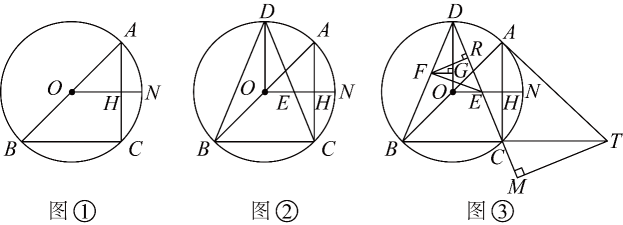 (1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.
(1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.五、综合题
-
12. 如图,是的直径,点是圆上的一点,于点 , 交于点 , 连接 , 若平分 , 过点作于点 , 交于点 , 延长 , 交于点 .
 (1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.
(1)、求证:是的切线;(2)、求证:;(3)、若 , 求的值.
-

