2023年黑龙江省中考数学真题分类汇编5 四边形
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 将两个完全相同的菱形按如图方式放置,若 , , 则( )
 A、 B、 C、 D、2. 下列说法正确的是( )A、一个函数是一次函数就一定是正比例函数 B、有一组对角相等的四边形一定是平行四边形 C、两条直角边对应相等的两个直角三角形一定全等 D、一组数据的方差一定大于标准差3. 如图,正方形的顶点A,B在y轴上,反比例函数的图象经过点C和的中点E,若 , 则k的值是( )
A、 B、 C、 D、2. 下列说法正确的是( )A、一个函数是一次函数就一定是正比例函数 B、有一组对角相等的四边形一定是平行四边形 C、两条直角边对应相等的两个直角三角形一定全等 D、一组数据的方差一定大于标准差3. 如图,正方形的顶点A,B在y轴上,反比例函数的图象经过点C和的中点E,若 , 则k的值是( )
 A、3 B、4 C、5 D、64. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
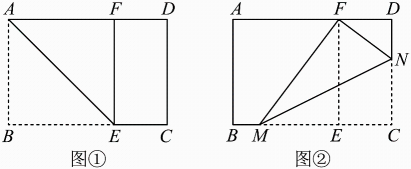
A、3 B、4 C、5 D、64. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折出一个正方形 , 然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕 , 如图②.
根据以上的操作,若 , , 则线段的长是( )
 A、3 B、 C、2 D、15. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( )
A、3 B、 C、2 D、15. 如图,在平面直角坐标中,矩形的边 , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是( ) A、 B、 C、 D、6. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( )
A、 B、 C、 D、6. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、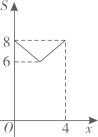 D、
D、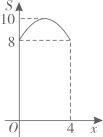 7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( )
7. 如图,在正方形中,点分别是上的动点,且 , 垂足为 , 将沿翻折,得到交于点 , 对角线交于点 , 连接 , 下列结论正确的是:①;②;③若 , 则四边形是菱形;④当点运动到的中点,;⑤ . ( ) A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
A、①②③④⑤ B、①②③⑤ C、①②③ D、①②⑤8. 如图,在正方形中,点E为边的中点,连接 , 过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为( )
① ② ③当时,
A、0个 B、1个 C、2个 D、3个9. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( ) A、
A、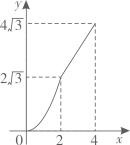 B、
B、 C、
C、 D、
D、 10. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
10. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )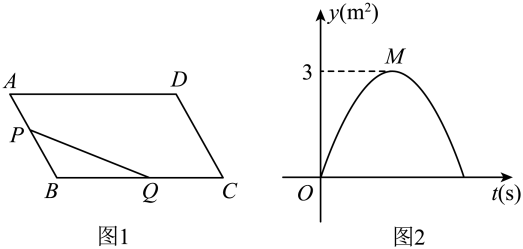 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
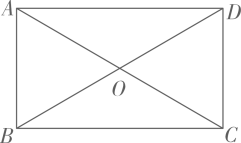
11. 如图,在矩形中对角线 , 交于点 , 请添加一个条件 , 使矩形是正方形(填一个即可)
 12. 如图,在四边形ABCD中, , 于点O.请添加一个条件: , 使四边形ABCD成为菱形.
12. 如图,在四边形ABCD中, , 于点O.请添加一个条件: , 使四边形ABCD成为菱形. 13. 如图在正方形中,点E在上,连接 , , F为的中点连接 . 若 , 则的长为 .
13. 如图在正方形中,点E在上,连接 , , F为的中点连接 . 若 , 则的长为 . 14. 矩形的对角线 , 相交于点 , 点在矩形边上,连接 . 若 , , 则 .15. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .
14. 矩形的对角线 , 相交于点 , 点在矩形边上,连接 . 若 , , 则 .15. 如图,在平面直角坐标系中,菱形的顶点A,B在x轴上, , , , 将菱形绕点A旋转后,得到菱形 , 则点的坐标是 .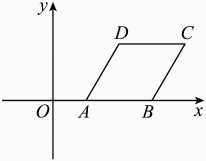 16. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 .
16. 如图,在正方形中,E在边上,交对角线于点F,于M,的平分线所在直线分别交 , 于点N,P,连接 . 下列结论:①;②;③;④若 , , 则 , 其中正确的是 . 17. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .18. 矩形纸片ABCD中, , , 点M在AD边所在的直线上,且 , 将矩形纸片ABCD折叠,使点B与点M重合,折痕与AD,BC分别交于点E,F,则线段EF的长度为.
17. 矩形中, , 将矩形沿过点的直线折叠,使点落在点处,若是直角三角形,则点到直线的距离是 .18. 矩形纸片ABCD中, , , 点M在AD边所在的直线上,且 , 将矩形纸片ABCD折叠,使点B与点M重合,折痕与AD,BC分别交于点E,F,则线段EF的长度为.三、解答题
-
19. 已知四边形是平行四边形,点在对角线上,点在边上,连接 , , .
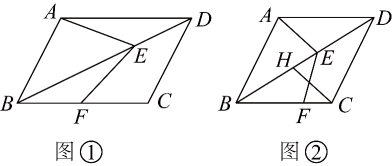 (1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.
(1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.四、综合题
-
20. 如图,在平行四边形中,为线段的中点,连接 , , 延长 , 交于点 , 连接 , .
 (1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.21. 中, , 垂足为E,连接 , 将绕点E逆时针旋转 , 得到 , 连接 .
(1)、求证:四边形是矩形;(2)、若 , , 求四边形的面积.21. 中, , 垂足为E,连接 , 将绕点E逆时针旋转 , 得到 , 连接 . (1)、当点E在线段上,时,如图①,求证:;(2)、当点E在线段延长线上,时,如图②:当点E在线段延长线上,时,如图③,请猜想并直接写出线段AE,EC,BF的数量关系;(3)、在(1)、(2)的条件下,若 , , 则 .22. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题:
(1)、当点E在线段上,时,如图①,求证:;(2)、当点E在线段延长线上,时,如图②:当点E在线段延长线上,时,如图③,请猜想并直接写出线段AE,EC,BF的数量关系;(3)、在(1)、(2)的条件下,若 , , 则 .22. 如图,在平面直角坐标系中,的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程的两个根().请解答下列问题: (1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.23. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.
(1)、求点B的坐标;(2)、若 , 直线分别交x轴、y轴、AD于点E,F,M,且M是AD的中点,直线EF交DC延长线于点N,求的值;(3)、在(2)的条件下,点P在y轴上,在直线EF上是否存在点Q,使是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q的坐标;若不存在,请说明理由.23. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.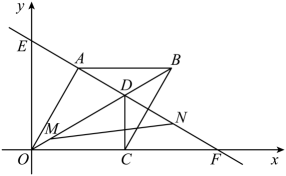 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.24. 已知:四边形为矩形, , , 点F是延长线上的一个动点(点F不与点C重合).连接交于点G.
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.24. 已知:四边形为矩形, , , 点F是延长线上的一个动点(点F不与点C重合).连接交于点G. (1)、如图一,当点G为的中点时,求证:.(2)、如图二,过点C作 , 垂足为E.连接 , 设 , .求y关于x的函数关系式.(3)、如图三,在(2)的条件下,过点B作 , 交的延长线于点M.当时,求线段的长.
(1)、如图一,当点G为的中点时,求证:.(2)、如图二,过点C作 , 垂足为E.连接 , 设 , .求y关于x的函数关系式.(3)、如图三,在(2)的条件下,过点B作 , 交的延长线于点M.当时,求线段的长.
-