2023年黑龙江省中考数学真题分类汇编4 三角形
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 如图,直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 则的度数是( )
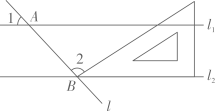 A、 B、 C、 D、2. 将两个完全相同的菱形按如图方式放置,若 , , 则( )
A、 B、 C、 D、2. 将两个完全相同的菱形按如图方式放置,若 , , 则( ) A、 B、 C、 D、3. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( )
A、 B、 C、 D、3. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( ) A、 B、 C、 D、4. 下列命题中叙述正确的是( )A、若方差 , 则甲组数据的波动较小 B、直线外一点到这条直线的垂线段,叫做点到直线的距离 C、三角形三条中线的交点叫做三角形的内心 D、角的内部到角的两边的距离相等的点在角的平分线上5. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )
A、 B、 C、 D、4. 下列命题中叙述正确的是( )A、若方差 , 则甲组数据的波动较小 B、直线外一点到这条直线的垂线段,叫做点到直线的距离 C、三角形三条中线的交点叫做三角形的内心 D、角的内部到角的两边的距离相等的点在角的平分线上5. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )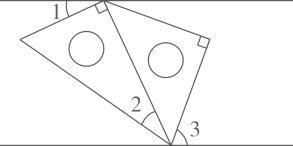 A、55° B、65° C、70° D、75°
A、55° B、65° C、70° D、75°二、填空题
-
6. 如图,在中,将绕点A顺时针旋转至 , 将绕点A逆时针旋转至 , 得到 , 使 , 我们称是的“旋补三角形”,的中线叫做的“旋补中线”,点A叫做“旋补中心”.下列结论正确的有 .
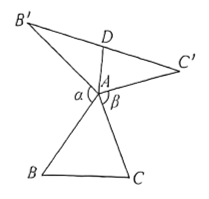
①与面积相同;
②;
③若 , 连接和 , 则;
④若 , , , 则 .
7. 如图, , 与交于点O,请添加一个条件 , 使 . (只填一种情况即可)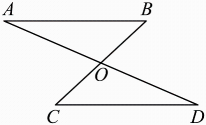 8. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .
8. 如图,将的按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,与尺下沿重合,与尺上沿的交点B在尺上的读数恰为 , 若按相同的方式将的放置在该刻度尺上,则与尺上沿的交点C在尺上的读数为 .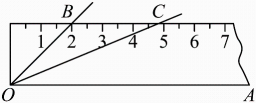 9. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
9. 在中, , 点是斜边的中点,把绕点顺时针旋转,得 , 点 , 点旋转后的对应点分别是点 , 点 , 连接 , , 在旋转的过程中,面积的最大值是 .
 10. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
10. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 . 11. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是.
11. 如图,是边长为6的等边三角形,点E为高上的动点.连接 , 将绕点C顺时针旋转60°得到.连接 , , , 则周长的最小值是. 12. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.
12. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.三、作图题
-
13. 如图,方格纸中每个小正方形的边长均为个单位长度,线段和线段的端点均在小正方形的顶点上.
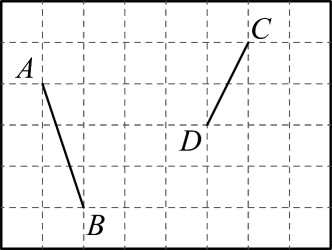 (1)、在方格纸中画出 , 且为钝角(点在小正方形的顶点上);(2)、在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点 , 点的对应点是点),连接 , 请直接写出线段的长.14. 在中, , , , D为的中点,以为直角边作含角的 , , 且点E与点A在的同侧,请用尺规或三角板作出符合条件的图形,并直接写出线段的长.15. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , .
(1)、在方格纸中画出 , 且为钝角(点在小正方形的顶点上);(2)、在方格纸中将线段向下平移个单位长度,再向右平移个单位长度后得到线段(点的对应点是点 , 点的对应点是点),连接 , 请直接写出线段的长.14. 在中, , , , D为的中点,以为直角边作含角的 , , 且点E与点A在的同侧,请用尺规或三角板作出符合条件的图形,并直接写出线段的长.15. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , . (1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).
(1)、将向上平移4个单位,再向右平移1个单位,得到 , 请画出 .(2)、请画出关于轴对称的 .(3)、将着原点顺时针旋转 , 得到 , 求线段在旋转过程中扫过的面积(结果保留).四、解答题
-
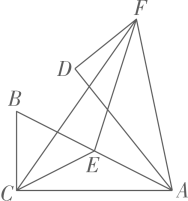
16. 如图①,和是等边三角形,连接 , 点F,G,H分别是和的中点,连接 . 易证: .
若和都是等腰直角三角形,且 , 如图②:若和都是等腰三角形,且 , 如图③:其他条件不变,判断和之间的数量关系,写出你的猜想,并利用图②或图③进行证明.

五、实践探究题
-
17. 综合与实践
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
 (1)、发现问题:如图1,在和中, , , , 连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: , °;(2)、类比探究:如图2,在和中, , , , 连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接BE,CF,且点B,E,F在一条直线上,过点A作 , 垂足为点M.则BF,CF,AM之间的数量关系:;(4)、实践应用:正方形ABCD中, , 若平面内存在点P满足 , , 则.
(1)、发现问题:如图1,在和中, , , , 连接BE,CF,延长BE交CF于点D.则BE与CF的数量关系: , °;(2)、类比探究:如图2,在和中, , , , 连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接BE,CF,且点B,E,F在一条直线上,过点A作 , 垂足为点M.则BF,CF,AM之间的数量关系:;(4)、实践应用:正方形ABCD中, , 若平面内存在点P满足 , , 则.
-