2023年黑龙江省中考数学真题分类汇编3 函数
试卷更新日期:2023-09-04 类型:二轮复习
一、选择题
-
1. 函数中,自变量x的取值范围是( )A、 B、 C、 D、2. 下列说法正确的是( )A、一个函数是一次函数就一定是正比例函数 B、有一组对角相等的四边形一定是平行四边形 C、两条直角边对应相等的两个直角三角形一定全等 D、一组数据的方差一定大于标准差3. 一条小船沿直线从码头向码头匀速前进,到达码头后,停留一段时间,然后原路匀速返回码头.在整个过程中,这条小船与码头的距离s(单位:)与所用时间(单位:)之间的关系如图所示,则这条小船从码头到码头的速度和从码头返回码头的速度分别为( )
 A、 B、 C、 D、4. 如图,正方形的顶点A,B在y轴上,反比例函数的图象经过点C和的中点E,若 , 则k的值是( )
A、 B、 C、 D、4. 如图,正方形的顶点A,B在y轴上,反比例函数的图象经过点C和的中点E,若 , 则k的值是( )
 A、3 B、4 C、5 D、65. 如图,抛物线经过点 , . 下列结论:①;②;③若抛物线上有点 , , , 则;④方程的解为 , , 其中正确的个数是( )
A、3 B、4 C、5 D、65. 如图,抛物线经过点 , . 下列结论:①;②;③若抛物线上有点 , , , 则;④方程的解为 , , 其中正确的个数是( )
 A、4 B、3 C、2 D、16. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( )
A、4 B、3 C、2 D、16. 如图,是等腰三角形,过原点 , 底边轴,双曲线过两点,过点作轴交双曲线于点 , 若 , 则的值是( ) A、 B、 C、 D、7. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( )
A、 B、 C、 D、7. 如图,在正方形ABCD中, , 动点M,N分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为 , 的面积为S,下列图象中能反映S与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、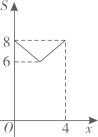 D、
D、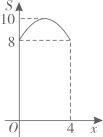 8. 如图,二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论:
8. 如图,二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论: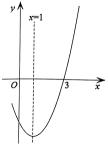
①;②;③;
④关于x的一元二次方程有两个不相等的实数根;
⑤若点 , 均在该二次函数图象上,则.其中正确结论的个数是( )
A、4 B、3 C、2 D、19. 在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B,C的横坐标都是3, , 点D在上,且其横坐标为1,若反比例函数()的图象经过点B,D,则k的值是( )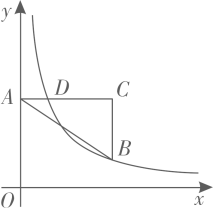 A、1 B、2 C、3 D、10. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( )
A、1 B、2 C、3 D、10. 如图,在菱形中, , , 动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( ) A、
A、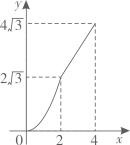 B、
B、 C、
C、 D、
D、 11. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )
11. 如图1,在平行四边形中, , 已知点在边上,以1m/s的速度从点向点运动,点在边上,以的速度从点向点运动.若点 , 同时出发,当点到达点时,点恰好到达点处,此时两点都停止运动.图2是的面积与点的运动时间之间的函数关系图象(点为图象的最高点),则平行四边形的面积为( )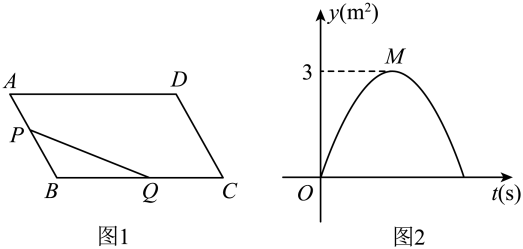 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 在函数中,自变量x的取值范围是 .13. 已知反比例函数的图象经过点 , 则a的值为 .14. 抛物线与y轴的交点坐标 .15. 将抛物线向下平移1个单位长度,再向右平移个单位长度后,得到的新抛物线经过原点.16. 如图,点A在反比例函数图象的一支上,点B在反比例函数图象的一支上,点C,D在x轴上,若四边形ABCD是面积为9的正方形,则实数k的值为.
 17. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)
17. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)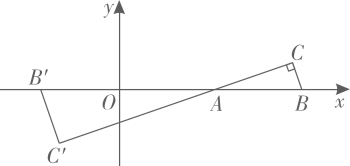 18. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 .
18. 如图,在平面直角坐标系中,的顶点A在直线上,顶点B在x轴上,垂直轴,且 , 顶点在直线上,;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第一个;过点作直线的垂线,垂足为 , 交x轴于 , 过点作垂直x轴,交于点 , 连接 , 得到第二个;如此下去,……,则的面积是 . 19. 如图,在平面直角坐标系中,点A在y轴上,点B在x轴上, , 连接AB,过点O作于点 , 过点作轴于点;过点作于点 , 过点作轴于点;过点作于点 , 过点作轴于点;…;按照如此规律操作下去,则点的坐标为.
19. 如图,在平面直角坐标系中,点A在y轴上,点B在x轴上, , 连接AB,过点O作于点 , 过点作轴于点;过点作于点 , 过点作轴于点;过点作于点 , 过点作轴于点;…;按照如此规律操作下去,则点的坐标为.
三、综合题
-
20. 一次函数与反比例函数的图象交于 , 两点,点的坐标为 .
 (1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.21. 某建筑物的窗户如图所示,上半部分是等腰三角形, , , 点、、分别是边、、的中点;下半部分四边形是矩形, , 制造窗户框的材料总长为16米(图中所有黑线的长度和),设米,米.
(1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、过动点作轴的垂线 , 与一次函数和反比例函数的图象分别交于 , 两点,当在的上方时,请直接写出的取值范围.21. 某建筑物的窗户如图所示,上半部分是等腰三角形, , , 点、、分别是边、、的中点;下半部分四边形是矩形, , 制造窗户框的材料总长为16米(图中所有黑线的长度和),设米,米. (1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.22. 如图,抛物线与x轴交于点 , , 与y轴交于点C.
(1)、求与之间的函数关系式,并求出自变量的取值范围;(2)、当为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.22. 如图,抛物线与x轴交于点 , , 与y轴交于点C. (1)、求抛物线对应的函数解析式,并直接写出顶点P的坐标;(2)、求的面积.
(1)、求抛物线对应的函数解析式,并直接写出顶点P的坐标;(2)、求的面积.注:抛物线的对称轴是直线 , 顶点坐标是 .
23. 在一条高速公路上依次有A,B,C三地,甲车从A地出发匀速驶向C地,到达C地休息后调头(调头时间忽略不计)按原路原速驶向B地,甲车从A地出发后,乙车从C地出发匀速驶向A地,两车同时到达目的地.两车距A地路程与甲车行驶时间之间的函数关系如图所示.请结合图象信息,解答下列问题: (1)、甲车行驶的速度是 , 乙车行驶的速度是 .(2)、求图中线段所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;(3)、乙车出发多少小时,两车距各自出发地路程的差是?请直接写出答案.24. 已知甲,乙两地相距 , 一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距 , 货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离与货车行驶时间之间的函数图象,结合图象回答下列问题:
(1)、甲车行驶的速度是 , 乙车行驶的速度是 .(2)、求图中线段所表示的y与x之间的函数解析式,并直接写出自变量x的取值范围;(3)、乙车出发多少小时,两车距各自出发地路程的差是?请直接写出答案.24. 已知甲,乙两地相距 , 一辆出租车从甲地出发往返于甲乙两地,一辆货车沿同一条公路从乙地前往甲地,两车同时出发,货车途经服务区时,停下来装完货物后,发现此时与出租车相距 , 货车继续出发后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图是两车距各自出发地的距离与货车行驶时间之间的函数图象,结合图象回答下列问题: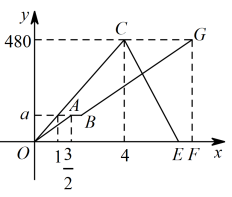 (1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .25. 2023年5月30日上午9点31分,神舟十六号载人飞船在酒泉发射中心发射升空,某中学组织毕业班的同学到当地电视台演播大厅观看现场直播,学校准备为同学们购进A,B两款文化衫,每件A款文化衫比每件B款文化衫多10元,用500元购进A款和用400元购进B款的文化衫的数量相同.(1)、求A款文化衫和B款文化衫每件各多少元?(2)、已知毕业班的同学一共有300人,学校计划用不多于14800元,不少于14750元购买文化衫,求有几种购买方案?(3)、在实际购买时,由于数量较多,商家让利销售,A款七折优惠,B款每件让利m元,采购人员发现(2)中的所有购买方案所需资金恰好相同,试求m值.26. 如图,抛物线与轴交于两点,交轴于点 .
(1)、图中的值是;(2)、求货车装完货物后驶往甲地的过程中,距其出发地的距离与行驶时间之间的函数关系式;(3)、直接写出在出租车返回的行驶过程中,货车出发多长时间与出租车相距 .25. 2023年5月30日上午9点31分,神舟十六号载人飞船在酒泉发射中心发射升空,某中学组织毕业班的同学到当地电视台演播大厅观看现场直播,学校准备为同学们购进A,B两款文化衫,每件A款文化衫比每件B款文化衫多10元,用500元购进A款和用400元购进B款的文化衫的数量相同.(1)、求A款文化衫和B款文化衫每件各多少元?(2)、已知毕业班的同学一共有300人,学校计划用不多于14800元,不少于14750元购买文化衫,求有几种购买方案?(3)、在实际购买时,由于数量较多,商家让利销售,A款七折优惠,B款每件让利m元,采购人员发现(2)中的所有购买方案所需资金恰好相同,试求m值.26. 如图,抛物线与轴交于两点,交轴于点 .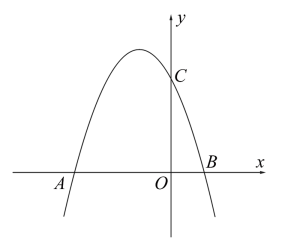 (1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.27. 一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地,小时后,一辆货车从A地出发,沿同一路线每小时行驶80千米匀速驶向B地,货车到达B地填装货物耗时15分钟,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、求抛物线的解析式.(2)、拋物线上是否存在一点 , 使得 , 若存在,请直接写出点的坐标;若不存在,请说明理由.27. 一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地,小时后,一辆货车从A地出发,沿同一路线每小时行驶80千米匀速驶向B地,货车到达B地填装货物耗时15分钟,然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y(千米)与货车出发时间x(小时)之间的函数关系如图所示,请结合图象解答下列问题: (1)、A,B两地之间的距离是千米,;(2)、求线段FG所在直线的函数解析式;(3)、货车出发多少小时两车相距15千米?(直接写出答案即可)28. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表:
(1)、A,B两地之间的距离是千米,;(2)、求线段FG所在直线的函数解析式;(3)、货车出发多少小时两车相距15千米?(直接写出答案即可)28. 如图,二次函数的图象与轴交于A , 两点,且自变量的部分取值与对应函数值如下表: (1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.29. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.
(1)、求二次函数的表达式;(2)、若将线段向下平移,得到的线段与二次函数的图象交于 , 两点(在左边),为二次函数的图象上的一点,当点的横坐标为 , 点的横坐标为时,求的值;(3)、若将线段先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数的图象只有一个交点,其中为常数,请直接写出的取值范围.29. 如图,在平面直角坐标系中,菱形的边在x轴上, , 的长是一元二次方程的根,过点C作x轴的垂线,交对角线于点D,直线分别交x轴和y轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿向终点D运动,动点N从点F以每秒2个单位长度的速度沿向终点E运动.两点同时出发,设运动时间为t秒.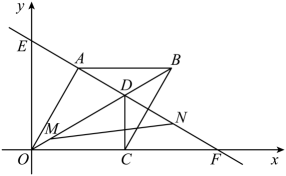 (1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.30. 某校组织师生参加夏令营活动,现准备租用A、B两型客车(每种型号的客车至少租用一辆).A型车每辆租金500元,B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人;3辆A型和4辆B型车坐满后共载客340人.(1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t为何值时两车相距25千米.
(1)、求直线的解析式.(2)、连接 , 求的面积S与运动时间t的函数关系式.(3)、点N在运动的过程中,在坐标平面内是否存在一点Q.使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.30. 某校组织师生参加夏令营活动,现准备租用A、B两型客车(每种型号的客车至少租用一辆).A型车每辆租金500元,B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人;3辆A型和4辆B型车坐满后共载客340人.(1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t为何值时两车相距25千米.
 31. 如图,抛物线的图象经过 , , 三点,且一次函数的图象经过点B.
31. 如图,抛物线的图象经过 , , 三点,且一次函数的图象经过点B.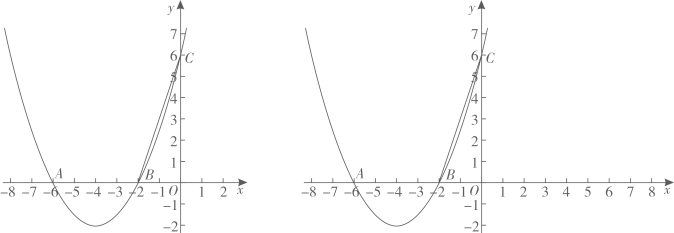 (1)、求抛物线和一次函数的解析式.(2)、点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的E,F两点是否存在?如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.(3)、将抛物线的图象向右平移8个单位长度得到抛物线 , 此抛物线的图象与x轴交于M,N两点(M点在N点左侧).点P是抛物线上的一个动点且在直线下方.已知点P的横坐标为m.过点P作于点D.求m为何值时,有最大值,最大值是多少?32. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , , 与轴交于点 .
(1)、求抛物线和一次函数的解析式.(2)、点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的E,F两点是否存在?如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.(3)、将抛物线的图象向右平移8个单位长度得到抛物线 , 此抛物线的图象与x轴交于M,N两点(M点在N点左侧).点P是抛物线上的一个动点且在直线下方.已知点P的横坐标为m.过点P作于点D.求m为何值时,有最大值,最大值是多少?32. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , , 与轴交于点 .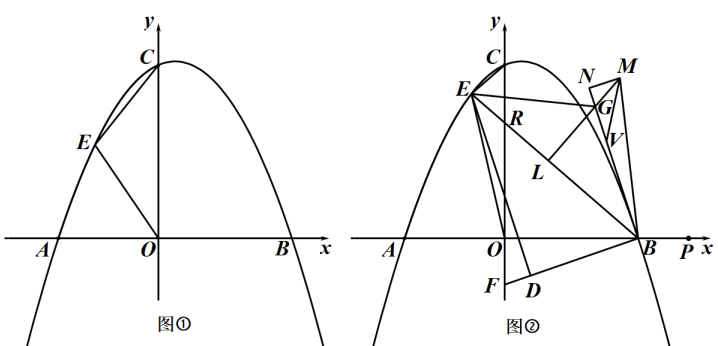 (1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.
(1)、求 , 的值;(2)、如图①,是第二象限抛物线上的一个动点,连接 , , 设点的横坐标为 , 的面积为 , 求关于的函数解析式(不要求写出自变量的取值范围);(3)、如图②,在(2)的条件下,当时,连接交轴于点 , 点在轴负半轴上,连接 , 点在上,连接 , 点在线段上(点不与点重合),过点作的垂线与过点且平行于的直线交于点 , 为的延长线上一点,连接 , , 使 , 是轴上一点,且在点的右侧, , 过点作 , 交的延长线于点 , 点在上,连接 , 使 , 若 , 求直线的解析式.四、实践探究题
-
33. 综合与探究
如图,抛物线上的点A,C坐标分别为 , , 抛物线与x轴负半轴交于点B,点M为y轴负半轴上一点,且 , 连接AC,CM.
 (1)、求点M的坐标及抛物线的解析式;(2)、点P是抛物线位于第一象限图象上的动点,连接AP,CP,当时,求点P的坐标;(3)、点D是线段BC(包含点B,C)上的动点,过点D作x轴的垂线,交抛物线于点Q,交直线CM于点N,若以点Q,N,C为顶点的三角形与相似,请直接写出点Q的坐标;(4)、将抛物线沿x轴的负方向平移得到新抛物线,点A的对应点为点 , 点C的对应点为点 , 在抛物线平移过程中,当的值最小时,新抛物线的顶点坐标为 , 的最小值为.
(1)、求点M的坐标及抛物线的解析式;(2)、点P是抛物线位于第一象限图象上的动点,连接AP,CP,当时,求点P的坐标;(3)、点D是线段BC(包含点B,C)上的动点,过点D作x轴的垂线,交抛物线于点Q,交直线CM于点N,若以点Q,N,C为顶点的三角形与相似,请直接写出点Q的坐标;(4)、将抛物线沿x轴的负方向平移得到新抛物线,点A的对应点为点 , 点C的对应点为点 , 在抛物线平移过程中,当的值最小时,新抛物线的顶点坐标为 , 的最小值为.