2023年黑龙江省中考数学真题分类汇编2 方程与不等式

试卷更新日期：2023-09-04 类型：二轮复习

进入出卷网下载

一、选择题

1. 方程 $\frac{2}{x} = \frac{3}{x + 1}$ 的解为（）

A、 $x = 1$ B、 $x = - 1$ C、 $x = 2$ D、 $x = - 2$

查看试题解析
2. 端午节是我国传统节日，端午节前夕，某商家出售粽子的标价比成本高25%，当粽子降价出售时，为了不亏本，降价幅度最多为（）

A、 $20 %$ B、 $25 %$ C、 $75 %$ D、 $80 %$

查看试题解析
3. 若分式方程 $\frac{a}{x + 2} = 1 - \frac{3}{x + 2}$ 的解为负数，则a的取值范围是（）

A、 $a < - 1$ 且 $a \neq - 2$ B、 $a < 0$ 且 $a \neq - 2$ C、 $a < - 2$ 且 $a \neq - 3$ D、 $a < - 1$ 且 $a \neq - 3$

查看试题解析
4. 某社区为了打造“书香社区”，丰富小区居民的业余文化生活，计划出资500元全部用于采购A，B，C三种图书，A种每本30元，B种每本25元，C种每本20元，其中A种图书至少买5本，最多买6本（三种图书都要买），此次采购的方案有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析
5. 已知关于x的分式方程 $\frac{m}{x - 2} + 1 = \frac{x}{2 - x}$ 的解是非负数，则 $m$ 的取值范围是（）

A、 $m \leq 2$ B、 $m \geq 2$ C、 $m \leq 2$ 且 $m \neq - 2$ D、 $m < 2$ 且 $m \neq - 2$

查看试题解析
6. 如果关于x的分式方程 $\frac{2 x - m}{x + 1} = 1$ 的解是负数，那么实数m的取值范围是（）

A、 $m < - 1$ B、 $m > - 1$ 且 $m \neq 0$ C、 $m > - 1$ D、 $m < - 1$ 且 $m \neq - 2$

查看试题解析
7. 如图，在长为 $100 m$ ，宽为 $50 m$ 的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是 $3600 m^{2}$ ，则小路的宽是（）

A、 $5 m$ B、 $70 m$ C、 $5 m$ 或 $70 m$ D、 $10 m$

查看试题解析
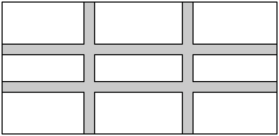8. 为提高学生学习兴趣，增强动手实践能力，某校为物理兴趣小组的同学购买了一根长度为150cm的导线，将其全部截成10cm和20cm两种长度的导线用于实验操作（每种长度的导线至少一根），则截取方案共有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析
9. 为了改善居民生活环境，云中小区对一块矩形空地进行绿化，这块空地的长比宽多6米，面积为720平方米，设矩形空地的长为x米，根据题意，所列方程正确的是（）

A、 $x (x - 6) = 720$ B、 $x (x + 6) = 720$ C、 $x (x - 6) = 360$ D、 $x (x + 6) = 360$

查看试题解析
10. 某运输公司，运送一批货物，甲车每天运送货物总量的 $\frac{1}{4}$ .在甲车运送1天货物后，公司增派乙车运送货物，两车又共同运送货物 $\frac{1}{2}$ 天，运完全部货物.求乙车单独运送这批货物需多少天？设乙车单独运送这批货物需x天，由题意列方程，正确的是（）

A、 $\frac{1}{4} + \frac{1}{2 x} = 1$ B、 $\frac{1}{4} + \frac{1}{2} (\frac{1}{4} + \frac{1}{x}) = 1$ C、 $\frac{1}{4} (1 + \frac{1}{2}) + \frac{1}{x} = 1$ D、 $\frac{1}{4} + (\frac{1}{4} + \frac{1}{2}) \frac{1}{x} = 1$

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} x + 2 > 3 (1 - x) \\ 1 - 2 x \leq 2 \end{array}$ 的解集是．

查看试题解析
12. 张师傅去年开了一家超市，今年2月份开始盈利，3月份盈利5000元，5月份盈利达到7200元，从3月到5月，每月盈利的平均增长率都相同，则每月盈利的平均增长率是．

查看试题解析
13. 关于 $x$ 的不等式组 ${\begin{array}{l} x + 5 > 0 \\ x - m \leq 1 \end{array}$ 有3个整数解，则实数 $m$ 的取值范围是．

查看试题解析
14. 已知一元二次方程 $x^{2} + x = 5 x + 6$ 的两根为 $x_{1}$ 与 $x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为.

查看试题解析
15. 若关于 $x$ 的不等式组 ${\begin{array}{l} 3 (x - 1) > x - 6 \\ 8 - 2 x + 2 a \geq 0 \end{array}$ 有三个整数解，则实数 $a$ 的取值范围为．

查看试题解析

三、计算题

16. 解方程： $x^{2} - 3 x + 2 = 0$

查看试题解析

四、解答题

17. 佳衣服装厂给某中学用同样的布料生产 $A$ ， $B$ 两种不同款式的服装，每套 $A$ 款服装所用布料的米数相同，每套 $B$ 款服装所用布料的米数相同，若 $1$ 套 $A$ 款服装和 $2$ 套 $B$ 款服装需用布料 $5$ 米， $3$ 套 $A$ 款服装和 $1$ 套 $B$ 款服装需用布料 $7$ 米．

(1)、求每套 $A$ 款服装和每套 $B$ 款服装需用布料各多少米；

(2)、该中学需要 $A$ ， $B$ 两款服装共 $100$ 套，所用布料不超过 $168$ 米，那么该服装厂最少需要生产多少套 $B$ 款服装？

查看试题解析
18. 为营造良好体育运动氛围，某学校用 $800$ 元购买了一批足球，又用 $1560$ 元加购了第二批足球，且所购数量是第一批购买数量的 $2$ 倍，但单价降了 $2$ 元，请问该学校两批共购买了多少个足球?

查看试题解析

五、综合题

19. 某商场欲购进A和B两种家电，已知B种家电的进价比A种家电的进价每件多100元，经计算，用1万元购进A种家电的件数与用1.2万元购进B种家电的件数相同．请解答下列问题：

(1)、这两种家电每件的进价分别是多少元？

(2)、若该商场欲购进两种家电共100件，总金额不超过53500元，且A种家电不超过67件，则该商场有哪几种购买方案？

(3)、在（2）的条件下，若A和B两种家电的售价分别是每件600元和750元，该商场从这100件中拿出两种家电共10件奖励优秀员工，其余家电全部售出后仍获利5050元，请直接写出这10件家电中B种家电的件数．

查看试题解析
20. 在一条高速公路上依次有A，B，C三地，甲车从A地出发匀速驶向C地，到达C地休息 $1 h$ 后调头（调头时间忽略不计）按原路原速驶向B地，甲车从A地出发 $1.5 h$ 后，乙车从C地出发匀速驶向A地，两车同时到达目的地．两车距A地路程 $y k m$ 与甲车行驶时间 $x h$ 之间的函数关系如图所示．请结合图象信息，解答下列问题：

(1)、甲车行驶的速度是 $k m / h$ ，乙车行驶的速度是 $k m / h$ ．

(2)、求图中线段 $M N$ 所表示的y与x之间的函数解析式，并直接写出自变量x的取值范围；

(3)、乙车出发多少小时，两车距各自出发地路程的差是 $160 k m$ ？请直接写出答案．

查看试题解析
21. 2023年5月30日上午9点31分，神舟十六号载人飞船在酒泉发射中心发射升空，某中学组织毕业班的同学到当地电视台演播大厅观看现场直播，学校准备为同学们购进A，B两款文化衫，每件A款文化衫比每件B款文化衫多10元，用500元购进A款和用400元购进B款的文化衫的数量相同．

(1)、求A款文化衫和B款文化衫每件各多少元？

(2)、已知毕业班的同学一共有300人，学校计划用不多于14800元，不少于14750元购买文化衫，求有几种购买方案？

(3)、在实际购买时，由于数量较多，商家让利销售，A款七折优惠，B款每件让利m元，采购人员发现（2）中的所有购买方案所需资金恰好相同，试求m值．

查看试题解析
22. 如图，在平面直角坐标系中， $▱ A B C D$ 的顶点B，C在x轴上，D在y轴上，OB，OC的长是方程 $x^{2} - 6 x + 8 = 0$ 的两个根（ $O B > O C$ ）．请解答下列问题：

(1)、求点B的坐标；

(2)、若 $O D ： O C = 2 ： 1$ ，直线 $y = - x + b$ 分别交x轴、y轴、AD于点E，F，M，且M是AD的中点，直线EF交DC延长线于点N，求 $t a n ∠ M N D$ 的值；

(3)、在（2）的条件下，点P在y轴上，在直线EF上是否存在点Q，使 $△ N P Q$ 是腰长为5的等腰三角形？若存在，请直接写出等腰三角形的个数和其中两个点Q的坐标；若不存在，请说明理由．

查看试题解析
23. 某校组织师生参加夏令营活动，现准备租用A、B两型客车（每种型号的客车至少租用一辆）.A型车每辆租金500元，B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人；3辆A型和4辆B型车坐满后共载客340人.

(1)、每辆A型车、B型车坐满后各载客多少人？

(2)、若该校计划租用A型和B型两种客车共10辆，总租金不高于5500元，并将全校420人载至目的地.该校有几种租车方案？哪种租车方案最省钱？

(3)、在这次活动中，学校除租用A、B两型客车外，又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米，甲车从学校出发0.5小时后，乙车才从学校出发，却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s（千米）与甲车行驶的时间t（小时）之间的函数图象.根据图象信息，求甲乙两车第一次相遇后，t为何值时两车相距25千米.

查看试题解析