贵州省铜仁市2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 四个有理数 , 0,1,中,最小的数是( )A、-1 B、0 C、1 D、-32. 下列调查中,最适合采用全面调查(普查)方式的是( )A、一批节能灯的使用寿命 B、对“神舟十六号”飞船零部件安全性的检查 C、对某品牌手机电池待机时间的调查 D、对中央电视台年春节联欢晚会满意度的调查3. 如图,七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板.下列由七巧板拼成的表情图中,是轴对称图形的为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在巴黎举行的第27届国际计量大会中,向国际单位制引进4个词头,、、和 . 其中,表示数字后有27个零,表示数字后有30个零.和则用于表示极小的数字,分别表示小数点后有27个零和30个零,引入后,地球质量可描述为约克,其中用科学记数法表示为( )A、 B、 C、 D、5. 下列运算中,正确的是( )A、 B、 C、 D、6. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )
4. 在巴黎举行的第27届国际计量大会中,向国际单位制引进4个词头,、、和 . 其中,表示数字后有27个零,表示数字后有30个零.和则用于表示极小的数字,分别表示小数点后有27个零和30个零,引入后,地球质量可描述为约克,其中用科学记数法表示为( )A、 B、 C、 D、5. 下列运算中,正确的是( )A、 B、 C、 D、6. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )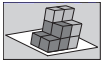 A、
A、 B、
B、 C、
C、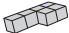 D、
D、 7. 为深入开展全民禁毒宣传教育,某校举行了禁毒知识竞赛.小红说:“我们班100分的同学最多,平均成绩是98分”.小红的描述所反映的统计量分别是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数8. 如图,若C为线段的中点,D在线段上, , , 则的长度是( )
7. 为深入开展全民禁毒宣传教育,某校举行了禁毒知识竞赛.小红说:“我们班100分的同学最多,平均成绩是98分”.小红的描述所反映的统计量分别是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数8. 如图,若C为线段的中点,D在线段上, , , 则的长度是( ) A、 B、1 C、 D、29. 若 , , 则的值为( )A、12 B、13 C、14 D、1510. 如图,直线AB∥CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是( )
A、 B、1 C、 D、29. 若 , , 则的值为( )A、12 B、13 C、14 D、1510. 如图,直线AB∥CD,GH平分∠CGF,GI平分∠DGF,且HG=15cm,GI=20cm,HI=25cm,则直线AB与直线CD之间的距离是( ) A、10cm B、12cm C、13cm D、14cm11. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,…,…,试问甜苦果几个,又问各该几个钱?若设买甜果x个,买苦果y个,列出符合题意的二元一次方程组: . 根据已有信息,题中用“…,…”表示的缺失的条件应为( )A、甜果九个十一文,苦果七个四文钱 B、甜果七个四文钱,苦果九个十一文 C、甜果十一个九文,苦果四个七文钱 D、甜果四个七文钱,苦果十一个九文12. 如图,用形状大小相同的菱形组成一组有规律的图案,其中第个图案中有个菱形,第个图案中有个菱形,第个图案中有个菱形,…按此规律排下去,若相邻的两个图案中菱形的个数共有个,则这两个图案分别是( )
A、10cm B、12cm C、13cm D、14cm11. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,…,…,试问甜苦果几个,又问各该几个钱?若设买甜果x个,买苦果y个,列出符合题意的二元一次方程组: . 根据已有信息,题中用“…,…”表示的缺失的条件应为( )A、甜果九个十一文,苦果七个四文钱 B、甜果七个四文钱,苦果九个十一文 C、甜果十一个九文,苦果四个七文钱 D、甜果四个七文钱,苦果十一个九文12. 如图,用形状大小相同的菱形组成一组有规律的图案,其中第个图案中有个菱形,第个图案中有个菱形,第个图案中有个菱形,…按此规律排下去,若相邻的两个图案中菱形的个数共有个,则这两个图案分别是( ) A、第个,第个 B、第个,第个 C、第个,第个 D、第个,第个
A、第个,第个 B、第个,第个 C、第个,第个 D、第个,第个二、填空题
-
13. 下列三个日常现象:

其中,可以用“垂线段最短”来解释的是 (填序号).
14. 如图,不添加辅助线,请写出一个能判定的条件 . 15. 如图,若四个完全相同的小直角三角形按如图方式全部放置在大直角三角形ABC的内部,这四个小三角形的斜边刚好相接在斜边上, , 则这四个小直角三角形的周长之和为 .
15. 如图,若四个完全相同的小直角三角形按如图方式全部放置在大直角三角形ABC的内部,这四个小三角形的斜边刚好相接在斜边上, , 则这四个小直角三角形的周长之和为 . 16. 如图,在长方形中, , , , 动点M在线段上运动(不与端点重合),点M关于边 , 的对称点分别为 , , 连接 , 点D在上,则在点M的运动过程中,线段长度的最小值是 .
16. 如图,在长方形中, , , , 动点M在线段上运动(不与端点重合),点M关于边 , 的对称点分别为 , , 连接 , 点D在上,则在点M的运动过程中,线段长度的最小值是 .
三、解答题
-
17. 计算:(1)、;(2)、解方程: .18. 因式分解:(1)、;(2)、 .19. 王老师在黑板上布置了一道题,小白和小红展开了下面的讨论:


已知时,求代数式:的值.
根据上述情景,你认为谁说得对?并将代数式化简求值.
20. 如图,的顶点都在方格纸的格点上.
⑴画出关于直线的对称图形;
⑵画出绕点逆时针旋转后并下移个单位得到的图形 .
21. 某市的出租车收费标准如下:起步价所允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.甲说:“我乘出租车走了千米,付车费元.”
乙说:“我乘出租车走了千米,付车费元.”
问:
(1)、出租车起步价是多少元?超过3千米的部分每千米收费多少元?(2)、小张乘出租车走了7千米,应付车费多少元?22. 如图,将绕点C顺时针旋转得到 , 使点A的对应点D落在边上.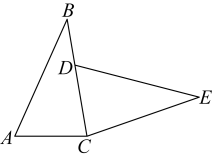 (1)、若 , , 求旋转的角度的大小;(2)、若 , , 求的长度.23. 教育部在落实“双减”的同时,推动“双增”,即增加学生参加户外活动、体育锻炼、艺术活动、劳动活动的时间和机会,增加学生接受体育和美育教育的时间和机会,确保学生的身心健康.甲、乙两名队员参加射击选拔赛,射击成绩见统计图:
(1)、若 , , 求旋转的角度的大小;(2)、若 , , 求的长度.23. 教育部在落实“双减”的同时,推动“双增”,即增加学生参加户外活动、体育锻炼、艺术活动、劳动活动的时间和机会,增加学生接受体育和美育教育的时间和机会,确保学生的身心健康.甲、乙两名队员参加射击选拔赛,射击成绩见统计图:
根据以上信息,整理分析数据如下:
队员
平均数(环)
中位数(环)
众数(环)
方差(环)
甲
7.9
b
c
4.09
乙
a
7
7
d
(1)、直接写出表格中a,b,c的值;(2)、求出d的值;(3)、若从甲、乙两名队员中选派其中一名队员参赛,你认为应选哪名队员?请结合表中的四个统计量,作出简要分析.24. “以形释数”是利用数形结合思想证明代数问题的一种体现,如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为的大正方形,2块是边长为的小正方形,5块是长为 , 宽为的相同的小长方形,且 . (1)、观察图2,可以发现代数式可以因式分解为;(2)、若图2中大长方形纸板的周长为 , 求的值;(3)、在(2)的条件下,若图2中阴影部分的面积为 , 求图中空白部分的面积.25. 如图
(1)、观察图2,可以发现代数式可以因式分解为;(2)、若图2中大长方形纸板的周长为 , 求的值;(3)、在(2)的条件下,若图2中阴影部分的面积为 , 求图中空白部分的面积.25. 如图 (1)、[操作发现]如图1,把一块含的直角三角板的边放置于长方形直尺的边上.请直接写出 , .(2)、[问题解决]如图 , 把三角板绕点逆时针旋转 , 当 , 点恰好落在边上时,求、的度数;(结果用含的代数式表示)(3)、[延伸探究]当时,是否存在三角板某一边所在的直线与直尺有四条边某一边所在的直线垂直?如果存在,请直接写出所有的值和对应的那两条垂线;如果不存在,请说明理由.
(1)、[操作发现]如图1,把一块含的直角三角板的边放置于长方形直尺的边上.请直接写出 , .(2)、[问题解决]如图 , 把三角板绕点逆时针旋转 , 当 , 点恰好落在边上时,求、的度数;(结果用含的代数式表示)(3)、[延伸探究]当时,是否存在三角板某一边所在的直线与直尺有四条边某一边所在的直线垂直?如果存在,请直接写出所有的值和对应的那两条垂线;如果不存在,请说明理由.