湖南省邵阳市新邵县2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、a2•a3=a6 B、(x3)2=x5 C、(2a)2=4a2 D、(x+1)2=x2+12. 第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京市和张家口市联合举办.以下是历届的冬奥会会徽设计的部分图形,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若二元一次方程组的解同时也是方程2x-my=-1的解,那么m的值为( )A、 B、 C、3 D、44. 如图,利用量角器测量角,则的大小为( )
3. 若二元一次方程组的解同时也是方程2x-my=-1的解,那么m的值为( )A、 B、 C、3 D、44. 如图,利用量角器测量角,则的大小为( )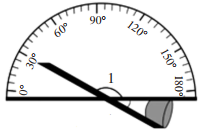 A、 B、 C、 D、5. 下列各组式子中,没有公因式的是( )A、-a2+ab与ab2-a2b B、mx+y与x+y C、(a+b)2与-a-b D、5m(x-y)与y-x6. 多项式可因式分解成 , 其中 , 均为整数,则的值为( )A、 B、1 C、 D、20237. 如图,在三角形中,点E,D,F分别在上,连接 , 下列条件中,能推理出的是( )
A、 B、 C、 D、5. 下列各组式子中,没有公因式的是( )A、-a2+ab与ab2-a2b B、mx+y与x+y C、(a+b)2与-a-b D、5m(x-y)与y-x6. 多项式可因式分解成 , 其中 , 均为整数,则的值为( )A、 B、1 C、 D、20237. 如图,在三角形中,点E,D,F分别在上,连接 , 下列条件中,能推理出的是( ) A、 B、 C、 D、8. 2023年4月23日是第28个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,小共这四项的得分依次为86、88、90、94,则她的最后得分是( )A、86分 B、88分 C、90分 D、94分9. 如图,将绕点按逆时针方向旋转得到 , 点的对应点是点 , 点的对应点是点 , 连接 , 若 , , 则的度数为( )
A、 B、 C、 D、8. 2023年4月23日是第28个世界读书日,某校举行了演讲大赛,演讲得分按“演讲内容”占、“语言表达”占、“形象风度”占、“整体效果”占进行计算,小共这四项的得分依次为86、88、90、94,则她的最后得分是( )A、86分 B、88分 C、90分 D、94分9. 如图,将绕点按逆时针方向旋转得到 , 点的对应点是点 , 点的对应点是点 , 连接 , 若 , , 则的度数为( ) A、 B、 C、 D、10. 装乒乓球的盒子有两种,大盒装6个,小盒装4个,若将50个乒乓球都装进盒子且把每个盒子都装满,那么不同的装球方法有( )A、3种 B、4种 C、5种 D、6种
A、 B、 C、 D、10. 装乒乓球的盒子有两种,大盒装6个,小盒装4个,若将50个乒乓球都装进盒子且把每个盒子都装满,那么不同的装球方法有( )A、3种 B、4种 C、5种 D、6种二、填空题
-
11. 分解因式:3a2﹣12= .12. 如图,与相交于点 , 若 , , 则 .
 13. 若 是一个完全平方式,则m的值为14. “冰墩墩”是北京2022年冬季奥运会的吉祥物,该吉祥物以能猫为原型进行设计创作,将熊猫形象与富有超能量的冰晶外壳相结合,体现了冬季冰雪运动和现代科技特点,冰墩墩玩具也很受欢迎.某玩具店一个星期销售冰墩墩玩具数量如下:
13. 若 是一个完全平方式,则m的值为14. “冰墩墩”是北京2022年冬季奥运会的吉祥物,该吉祥物以能猫为原型进行设计创作,将熊猫形象与富有超能量的冰晶外壳相结合,体现了冬季冰雪运动和现代科技特点,冰墩墩玩具也很受欢迎.某玩具店一个星期销售冰墩墩玩具数量如下:星期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
玩具数是(件)
35
47
50
60
42
48
68
则这个星期该玩具店销售冰墩墩玩具的中位数是 .
15. 已知:如图,直线BO⊥AO于点O,OB平分∠COD,∠BOD=22°.则∠AOC的度数是 度. 16. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.
16. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.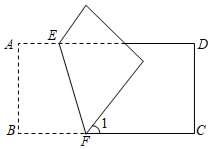 17. 若 , , 则多项式的值是 .
17. 若 , , 则多项式的值是 .三、解答题
-
18. 如图,在中, , . 垂足为 , , , , 则点到直线的距离为cm.
 19. 如图,在方格纸(边长为1个单位长)上,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:
19. 如图,在方格纸(边长为1个单位长)上,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:
⑴将格点△ABC绕A点逆时针旋转90°,得到△;
⑵将△沿直线作轴对称得到△;再将△向下平移3个单位得到△
20. 解下列方程组:(1)、;(2)、 .21. 已知(1)、求 , 的值.(2)、先化简,再求值: .22. 如图,已知:∠1+∠2=180°,∠3=∠A,求证:∠B=∠C. 23. 一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共元;若先请甲组单独做6天,再请乙组单独做天可以完成,需付给两组费用共元,问:(1)、甲、乙两组单独工作一天,商店应各付多少元?(2)、已知甲组单独完成需要天,乙组单独完成需要天,若装修完后,商店每天可盈利元,你认为如何安排施工有利于商店经营?说说你的理由.(提示:三种施工方式:方式一甲单独完成;方式二乙组单独完成;方式三甲、乙两个装修组同时施工.)24. 某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
23. 一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共元;若先请甲组单独做6天,再请乙组单独做天可以完成,需付给两组费用共元,问:(1)、甲、乙两组单独工作一天,商店应各付多少元?(2)、已知甲组单独完成需要天,乙组单独完成需要天,若装修完后,商店每天可盈利元,你认为如何安排施工有利于商店经营?说说你的理由.(提示:三种施工方式:方式一甲单独完成;方式二乙组单独完成;方式三甲、乙两个装修组同时施工.)24. 某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.a.甲、乙两位同学得分的折线图:

b.丙同学得分:10,10,10,9,9,8,3,9,8,10
c.甲、乙、丙三位同学得分的平均数:
同学
甲
乙
丙
平均数
根据以上信息,回答下列问题:
(1)、求表中的值;(2)、如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀.据此推断:在甲、乙、丙三位同学中,表现最优秀的是哪一位?(3)、在参加比赛的同学中,如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致.据此推断:甲、乙两位同学中,评委对谁的评价更一致?25. 如图1,点 , , 依次在直线上,现将射线绕点沿顺时针方向以每秒的速度转动,同时射线绕点沿逆时针方向以每秒的速度转动,直线保持不动,如图2,设转动时间为( , 单位:秒) (1)、当时,求的度数;(2)、在转动过程中,当第二次达到时,求的值;(3)、在转动过程中是否存在这样的 , 使得射线与射线垂直?如果存在,请求出的值:如果不存在,请说明理由.
(1)、当时,求的度数;(2)、在转动过程中,当第二次达到时,求的值;(3)、在转动过程中是否存在这样的 , 使得射线与射线垂直?如果存在,请求出的值:如果不存在,请说明理由.