江西省九江市2022-2023学年七年级下学期6月期末数学试题
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 下列大学校徽图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某种芯片每个探针单元的面积为 , 0.00000705用科学记数法可表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是( )
2. 某种芯片每个探针单元的面积为 , 0.00000705用科学记数法可表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是( ) A、 B、 C、 D、5. 如图,已知 , 那么下列结论一定正确的是( )
A、 B、 C、 D、5. 如图,已知 , 那么下列结论一定正确的是( )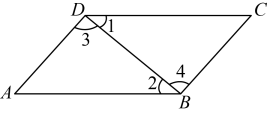 A、 B、 C、 D、6. 如图,在中,的垂直平分线交于点 , 交于点 , 平分 , 则的度数为( )
A、 B、 C、 D、6. 如图,在中,的垂直平分线交于点 , 交于点 , 平分 , 则的度数为( )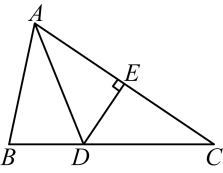 A、 B、 C、 D、7. 跳伞运动员从高空跳下,打开降落伞,最后安全着地,在这个过程中,跳伞运动员到地面的距离与时间的大致图象是( )A、
A、 B、 C、 D、7. 跳伞运动员从高空跳下,打开降落伞,最后安全着地,在这个过程中,跳伞运动员到地面的距离与时间的大致图象是( )A、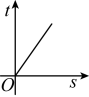 B、
B、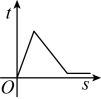 C、
C、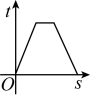 D、
D、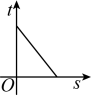 8. 已知(2x+k)2=4x2-12x+9,则k的值为( )A、3 B、±3 C、-3 D、±9
8. 已知(2x+k)2=4x2-12x+9,则k的值为( )A、3 B、±3 C、-3 D、±9二、填空题
-
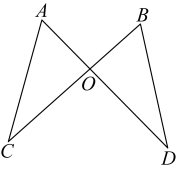
9. “任意掷一枚图钉,落地后针尖朝上”是事件(填“必然”,“随机”或“不可能”).10. 如图,已知与交于点, , 要使 , 添加一个你认为合适的条件为 .
 11. 某剧院的观众席的座位为扇形,且按下列方式设置:写出座位数y与排数x之间的关系式
11. 某剧院的观众席的座位为扇形,且按下列方式设置:写出座位数y与排数x之间的关系式排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
12. 已知 , 则 .13. 已知中是钝角,以所在直线为对称轴作 , 若 , 则的度数为 .14. 如果 , 那么 .15. 如图,为的中线,分别为 , 的一条高,若 , 则 .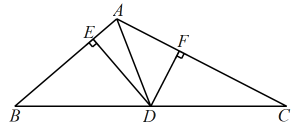 16. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)
16. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)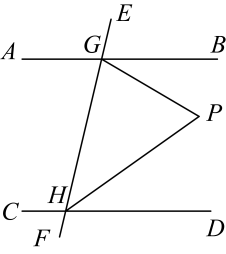
三、解答题
-
17. 计算: .18. 已知:如图, . 试说明: . 阅读下面的推理过程,请在括号内填写合适的理由,并将横线上的空补充完整.
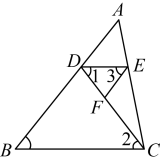
解:因为
所以( )
所以 ▲ ( )
又因为 , 所以 ▲ (等量代换)
所以( )
19. 如图,转盘被等分成6个扇形,分别标有数字1,3,5,6,8,9,甲转动指针,乙猜指针会停在哪一个数上,猜对了乙获胜,猜错了甲获胜.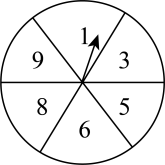 (1)、这个游戏中乙获胜的概率是多少?(2)、请设计一种对甲乙双方都公平的游戏方案,并简要说明.20. 先化简,再求值: , 其中 .21. 已知在同一平面内的两条相等线段,通过一次或两次轴对称变化就可以重合.如图方格纸中的每个小方格都是边长为1个单位长度的正方形,点都在格点上,请分别在下面两个图中画出对称轴,使得线段通过轴对称变化与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
(1)、这个游戏中乙获胜的概率是多少?(2)、请设计一种对甲乙双方都公平的游戏方案,并简要说明.20. 先化简,再求值: , 其中 .21. 已知在同一平面内的两条相等线段,通过一次或两次轴对称变化就可以重合.如图方格纸中的每个小方格都是边长为1个单位长度的正方形,点都在格点上,请分别在下面两个图中画出对称轴,使得线段通过轴对称变化与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段. 22. 如图,在中, , 点为上一点,且交于点 .
22. 如图,在中, , 点为上一点,且交于点 . (1)、试说明;(2)、猜想的度数并证明.23. 小海从家出发步行上学,途中发现没带语文书,小海打电话请父亲送书,父亲沿着同样的路线立即从家出发,5分钟后与原地等待的小海相遇,小海拿到书后加快速度去学校,父亲以原速返回家中.在整个过程中,小海与父亲之间的距离与小海离家的时间的对应关系如图所示.
(1)、试说明;(2)、猜想的度数并证明.23. 小海从家出发步行上学,途中发现没带语文书,小海打电话请父亲送书,父亲沿着同样的路线立即从家出发,5分钟后与原地等待的小海相遇,小海拿到书后加快速度去学校,父亲以原速返回家中.在整个过程中,小海与父亲之间的距离与小海离家的时间的对应关系如图所示.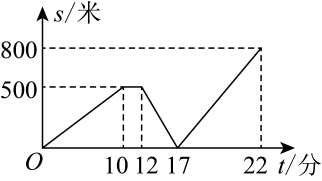
观察图象,回答下列问题:
(1)、图中自变量是 , 因变量是;(2)、小海家距离学校米;(3)、父亲的速度为米/分;(4)、小海加速前平均每分钟走多少米?加速后平均每分钟走多少米?24. 综合实践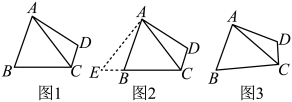
问题提出
如图1,在四边形中,与互补,与互补, , , , 数学兴趣小组在探究与的数量关系时,经历了如下过程:
(1)、实验操作数学兴趣小组通过电脑软件“几何画板”进行探究,测量出部分结果如下表所示:
这里 , , .
(2)、猜想证明根据表格,猜想:与之间的关系式为 ▲ ;数学兴趣小组发现证明此猜想的一种方法:如图2,延长到 , 使 , 连接 , ……,请你根据其思路将证明过程补充完整.
(3)、应用拓广如图3,若 , 求四边形的面积.