湖南省长沙市长郡教育集团2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 若 , 则下列结论错误的是( )A、 B、 C、 D、2. 如图,直线l1∥l2 , 直线l1、l2被直线l3所截,若∠1=54°,则∠2的大小为( )
 A、36° B、46° C、126° D、136°3. 平面直角坐标系中,在第二象限的点是( )A、 B、 C、 D、4. 下列调查中,最适合采用普查方式的是( )A、环保部门调查长江的水质情况 B、调查五一期间到扬州旅游的游客满意度 C、调查我市中学生使用手机的时长 D、调查神舟飞船各零件部位是否正常5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,下列推理不正确的是( )
A、36° B、46° C、126° D、136°3. 平面直角坐标系中,在第二象限的点是( )A、 B、 C、 D、4. 下列调查中,最适合采用普查方式的是( )A、环保部门调查长江的水质情况 B、调查五一期间到扬州旅游的游客满意度 C、调查我市中学生使用手机的时长 D、调查神舟飞船各零件部位是否正常5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,下列推理不正确的是( ) A、∵ , ∴ B、∵ , ∴ C、∵ , ∴ D、∵ , ∴7. 如果方程组的解为那么被“★”“■”遮住的两个数分别为( )A、3,10 B、4,10 C、10,4 D、10,38. 不等式组的解集在数轴上表示正确的是( )A、
A、∵ , ∴ B、∵ , ∴ C、∵ , ∴ D、∵ , ∴7. 如果方程组的解为那么被“★”“■”遮住的两个数分别为( )A、3,10 B、4,10 C、10,4 D、10,38. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 9. 若关于x,y的方程组的解满足 , 则k的值为( )A、2020 B、2021 C、2022 D、202310. 如图,在平面直角坐标系中,轴,轴,点D、C、P、H在x轴上, , , , , , 把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( )
9. 若关于x,y的方程组的解满足 , 则k的值为( )A、2020 B、2021 C、2022 D、202310. 如图,在平面直角坐标系中,轴,轴,点D、C、P、H在x轴上, , , , , , 把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,点与点间的距离是 .12. 如果关于 , y的方程是二元一次方程,那么 .13. 若 , 则的平方根是 .14. 已知关于的不等式的解集如图所示,则的值等于
 15. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为.16. 如图
15. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为.16. 如图 (1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .
(1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .三、解答题
-
17. 计算: .18. 解二元一次方程组: .19. 解下列不等式(组):(1)、;(2)、20. 如图,在边长均为1个单位长度的正方形网格图中,建立了平面直角坐标系 , 的顶点都在格点上,按要求解答下列问题:
 (1)、画出向右平移6个单位长度后,再向下平移2个单位长度后的图形;(2)、写出顶点 , , 的坐标;(3)、求线段所扫过的面积.21. 为落实“双减”政策,切实减轻学生学业负担,丰富学生课余生活,某校积极开展“五育并举”课外兴趣小组活动,计划成立“爱心传递”、“音乐舞蹈”、“体育运动”、“美工制作”和“劳动体验”五个兴趣小组,要求每位学生都只选其中一个小组.为此,随机抽查了本校各年级部分学生选择兴趣小组的意向,并将抽查结果绘制成如下统计图(不完整).
(1)、画出向右平移6个单位长度后,再向下平移2个单位长度后的图形;(2)、写出顶点 , , 的坐标;(3)、求线段所扫过的面积.21. 为落实“双减”政策,切实减轻学生学业负担,丰富学生课余生活,某校积极开展“五育并举”课外兴趣小组活动,计划成立“爱心传递”、“音乐舞蹈”、“体育运动”、“美工制作”和“劳动体验”五个兴趣小组,要求每位学生都只选其中一个小组.为此,随机抽查了本校各年级部分学生选择兴趣小组的意向,并将抽查结果绘制成如下统计图(不完整).
根据统计图中的信息,解答下列问题:
(1)、求本次被抽查学生的总人数和扇形统计图中表示“美工制作”的扇形的圆心角度数;(2)、将条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(3)、该校共有1600名学生,根据抽查结果,试估计全校选择“爱心传递”兴趣小组的学生人数.22. 完成下面的证明.已知:如图, , .
求证: .
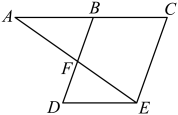
证明:∵( ),
(已知),
∴
∴∥ ▲ (同旁内角互补,两直线平行).
∴ ▲ (两直线平行,同位角相等).
∵(已知),
∴( ),
∴( ).
∴( ).
23. 如图,已知 , 于点 , . (1)、求证:;(2)、连接 , 若 , 且 , 求的度数.24. 为了响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,某中学购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A、B两种品牌足球的单价各多少元?(2)、根据需要,学校决定再次购进A、B两种品牌的足球50个,正逢体育用品商店“优惠促销”活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打8折.如果此次学校购买A、B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于23个,则有几种购买方案?为了节约资金,学校应选择哪种方案?25. 阅读材料并回答下列问题:
(1)、求证:;(2)、连接 , 若 , 且 , 求的度数.24. 为了响应习主席提出的“足球进校园”的号召,开设了“足球大课间活动”,某中学购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A、B两种品牌足球的单价各多少元?(2)、根据需要,学校决定再次购进A、B两种品牌的足球50个,正逢体育用品商店“优惠促销”活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打8折.如果此次学校购买A、B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于23个,则有几种购买方案?为了节约资金,学校应选择哪种方案?25. 阅读材料并回答下列问题:当m,n都是实数,且满足 , 就称点为“郡麓点”.例如:点 , 令 , 得 , , 所以不是“郡麓点”;点 , 令 , 得 , 所以是“郡麓点”.
(1)、请判断点点 , 是否为“郡麓点”:;(2)、若以关于x,y的方程组的解为坐标的点是“郡麓点”,求的值;(3)、若以关于x,y的方程组的解为坐标的点是“郡麓点”,求正整数a,b的值.26. 如图,在平面直角坐标系中,轴,垂足为A,轴,垂足为C,已知 , C(0,c),其中a,c满足关系式 . (1)、点P从O点出发沿折线的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为秒.
(1)、点P从O点出发沿折线的方向运动到点C停止,运动的速度为每秒2个单位长度,设点P的运动时间为秒.①在运动过程中,当点P到的距离为2个单位长度时, ▲ ;
②在点P的运动过程中,记的面积为S,用含t的代数式表示S;
(2)、点P在射线上,点M为射线上一动点, , 连接MC,作平分交x轴于点 , 直线上取点N,连接 , 使 , 当时,求的大小.