山西省临汾市洪洞县2022-2023学年七年级下学期7月期末数学试题

试卷更新日期：2023-09-04 类型：期末考试

进入出卷网下载

一、单选题

1. 剪纸艺术是中华民族的瑰宝，下面剪纸作品中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $a < b$ ，下列四个不等式中，正确的是（）

A、 $3 a > 3 b$ B、 $- 5 a < - 5 b$ C、 $a - 4 < b - 4$ D、 $2 - a < 2 - b$

查看试题解析
3. 如图，一扇窗户打开后，用窗钩 $A B$ 可将其固定，这里所运用的几何原理是（）

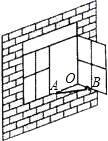A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短

查看试题解析
4. 已知三角形的两边分别为1和4，第三边长为整数，则该三角形的周长为（）

A、7 B、8 C、9 D、10

查看试题解析
5. 一个n边形的内角和比其外角和的2倍多 $180 °$ ，则n的值是（）

A、7 B、6 C、5 D、4

查看试题解析
6. 如图，直线 $a ∥ b$ ，若 $∠ 1 = 110 °$ ， $∠ 2 = 40 °$ ，则 $∠ 3$ 的度数是（）

A、 $55 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
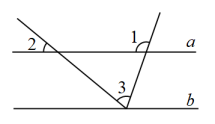7. 一个不等式组的解集在数轴上表示如图，则这个不等式组可能是（）

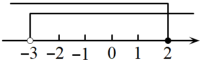A、 ${\begin{array}{l} - 2 x < 6 \\ x \geq 2 \end{array}$ B、 ${\begin{array}{l} - 2 x > 6 \\ x \leq 2 \end{array}$ C、 ${\begin{array}{l} - 2 x > 6 \\ x \geq 2 \end{array}$ D、 ${\begin{array}{l} - 2 x < 6 \\ x \leq 2 \end{array}$

查看试题解析
8. 如图，已知钝角三角形ABC，将△ABC绕点A按逆时针方向旋转110°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（）

A、55° B、65° C、75° D、85°

查看试题解析
9. 如图，已知 $Δ A B C$ 是正三角形， $D$ 是 $B C$ 边上任意一点，过点 $D$ 作 $D F ⊥ A C$ 于点 $F$ ， $E D ⊥ B C$ 交 $A B$ 于点 $E$ ，则 $∠ E D F$ 等于（）

A、 $50 °$ B、 $65 °$ C、 $60 °$ D、 $75 °$

查看试题解析
10. 在数学著作《九章算术》中有这样一个问题：“今有牛五，羊二，值金十两；牛二羊五，值金八两，问牛羊各值金几何？”译文：五头牛和两只羊共值金10两，两头牛和五只羊共值金8两，问牛和羊各值金多少两？若设一头牛值金x两，一只羊值金y两，可列方程组为（）

A、 ${\begin{array}{l} 5 x + 2 y = 10 \\ 2 x + 5 y = 8 \end{array}$ B、 ${\begin{array}{l} 5 x + 2 y = 10 \\ 2 x - 5 y = 8 \end{array}$ C、 ${\begin{array}{l} 5 x + 2 y = 10 \\ 2 y + 5 x = 8 \end{array}$ D、 ${\begin{array}{l} 5 x - 2 y = 10 \\ 2 y + 5 x = 8 \end{array}$

查看试题解析

二、填空题

11. 已知关于x的方程2x+a﹣5=0的解是x=2，则a的值为．

查看试题解析
12. 如图， $△ D E F$ 是由 $△ A B C$ 平移得到的，若 $B C = 3$ ， $A D = 2$ ，则 $E F =$ ．

查看试题解析
13. 在中国共青团建团100周年时，小明同学为留守儿童捐赠了一个书包．已知一个书包标价58元，现在打折出售，支付时还可以再减免3元，小明实际支付了43.4元，若设打了x折，则根据题意可列方程为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ， $C E ⊥ A B$ 于点 $E$ ，若 $∠ B = 50 °$ ， $∠ A C E = 20 °$ ，则 $∠ A D C$ 的度数是．

查看试题解析
15. 在关于x，y的方程组 ${\begin{array}{l} 2 x + y = m + 7 \\ x + 2 y = 8 - m \end{array}$ 中，未知数 $x \geq 0$ ， $y < 0$ ，那么m的取值范围是．

查看试题解析

三、解答题

16.

(1)、解一元一次方程：
      $\frac{x + 2}{4} - \frac{2 x - 1}{6} = 1$

(2)、解方程组：
      ${\begin{array}{l} 2 x + 3 y = 1 ① \\ x - 3 y = 6 ② \end{array}$

(3)、解不等式组： ${\begin{array}{l} 2 x - 6 < 3 x ① \\ \frac{x + 2}{3} - \frac{x - 1}{2} \geq 1 ② \end{array}$ 并将解集在数轴上表示出来．

查看试题解析
17. 课堂上，老师设计了“接力游戏”，规则：一列同学每人只完成解不等式的一步变形，即前一个同学完成一步，后一个同学接着前一个同学的步骤进行下一步变形，直至解出不等式的解集．请根据下面的“接力游戏”回答问题．

(1)、任务一：①在“接力游戏”中，乙同学是根据进行变形的．
A．等式的基本性质
B．不等式的基本性质
C．乘法对加法的分配律
②在“接力游戏”中，出现错误的是同学，这一步错误的原因是．

(2)、任务二：在“接力游戏”中该不等式的正确解集是．

(3)、任务三：除纠正上述错误外，请你根据平时的学习经验，针对解不等式时还需要注意的事项给同学们提一条建议．
接力游戏
老师 $\frac{3 x + 1}{2} - 1 > \frac{5 x - 4}{3}$
甲同学 $3 (3 x + 1) - 6 > 2 (5 x - 4)$
乙同学 $9 x + 3 - 6 > 10 x - 8$
丙同学 $9 x - 10 x > - 8 - 3 + 6$
丁同学 $- x > - 5$
戊同学 $x > 5$

查看试题解析
18. 将一副三角板拼成如图所示的图形，过点 $C$ 作 $C F$ 平分 $∠ D C E$ 交 $D E$ 于点 $F ．$

(1)、判断 $C F$ 与 $A B$ 的位置关系，并说明理由；

(2)、求 $∠ D F C$ 的度数．

查看试题解析
19. 如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．

(1)、将△ABC向上平移6个单位，再向右平移2个单位，得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ﹔

(2)、以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到 $△ A_{2} B_{2} C_{2}$ ，请画出 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
20. 如图，在 $△ A B C$ 中，将 $△ A C B$ 沿直线 $M N$ 折叠，使点 $C$ 与点 $B$ 重合，连接 $B M$ ．

(1)、若 $∠ A = 80 °$ ， $∠ C = 40 °$ ，求 $∠ A B M$ 的度数；

(2)、若 $A B = 5$ ， $A C = 8$ ，求 $△ A B M$ 的周长．

查看试题解析

21. 如上表，方程①、方程②、方程③、方程④．．．．是按照一定规律排列的一列方程：

序号	方程	方程的解
①	$2 (x - 2) - 3 (x - 1) = 1$	$x = - 2$
②	$2 (x - 2) - 3 (x - 2) = 2$	$x = 0$
③	$2 (x - 2) - 3 (x - 3) = 3$	$x =$ ____
④	$2 (x - 2) - 3 (x - 4) = 4$	$x =$ ____
…	…	…

(1)、将上表补充完整，

(2)、按上述方程所包含的某种规律写出方程⑤及其解；

(3)、写出表内这列方程中的第n（n为正整数）个方程和它的解．

查看试题解析

22. 某爱心企业在政府的支持下投入资金，准备修建一批室外简易的足球场和篮球场，供市民免费使用，修建1个足球场和1个篮球场共需8.5万元，修建2个足球场和4个篮球场共需27万元．

(1)、求修建一个足球场和一个篮球场各需多少万元？

(2)、该企业预计修建这样的足球场和篮球场共20个，投入资金不超过90万元，求至少可以修建多少个足球场？

查看试题解析
23. 在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D$ ．

特例研究：

(1)、如图1，若 $∠ B A C$ 的平分线 $A E$ 能交 $B C$ 于点 $E$ ， $∠ B = 35 °$ ， $∠ E A D = 5 °$ ，求 $∠ C$ 的度数；

(2)、操作发现：

如图2，点 $M$ ， $N$ 分别在线段 $A B$ ， $A C$ ，将 $△ A B C$ 折叠，点 $B$ 落在点 $F$ 处，点 $C$ 落在点 $G$ 处，折痕分别为 $D M$ 和 $D N$ ，点 $G$ ， $F$ 都在射线 $D A$ 上
若 $∠ B + ∠ C = 60 °$ ，试猜想 $∠ A M F$ 与 $∠ A N G$ 之间的数量关系，并说明理由

(3)、将 $△ D F M$ 绕点 $D$ 逆时针旋转，旋转角记为 $α$ （ $0 ° < α < 360 °$ ）．记旋转中的 $△ D M F$ 为 $△ D M_{1} F_{1}$ ，在旋转过程中，点 $M$ ， $F$ 的对应点分别为 $M_{1}$ ， $F_{1}$ ，直线 $M_{1} F_{1}$ ，与直线 $B C$ 交于点 $Q$ ，与直线 $A B$ 交于点 $P$ ．若 $∠ B = 35 °$ ， $∠ P Q B = 90 °$ ，请直接写出旋转角 $α$ 的度数．

查看试题解析