山西省运城市盐湖区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 每年三月份最后一周的星期一是全国中小学生安全教育日,为了警示学生,学校的许多场地都张贴了安全标志,下面是部分安全标志的图片,其文字上方的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 中国宝武太原钢铁集团生产的手撕钢,比纸薄,光如镜,质地还很硬,厚度仅0.0000015米,是世界上最薄的不锈钢,再次向世界展示了中国的创造能力数据“0.0000015”用科学记数法表示为( )A、 B、 C、 D、4. 下列说法正确的是( )A、某彩票的中奖概率是 , 那么如果买100张彩票一定会有5张中奖 B、两条直线被第三条直线所截,同位角相等 C、因为 , , 所以长度为5,8,14的三条线段可以围成三角形 D、任意画一条线段,一定是轴对称图形5. 如图,在平面内,一组平行线穿过 , 若 , , 则的度数是( )
3. 中国宝武太原钢铁集团生产的手撕钢,比纸薄,光如镜,质地还很硬,厚度仅0.0000015米,是世界上最薄的不锈钢,再次向世界展示了中国的创造能力数据“0.0000015”用科学记数法表示为( )A、 B、 C、 D、4. 下列说法正确的是( )A、某彩票的中奖概率是 , 那么如果买100张彩票一定会有5张中奖 B、两条直线被第三条直线所截,同位角相等 C、因为 , , 所以长度为5,8,14的三条线段可以围成三角形 D、任意画一条线段,一定是轴对称图形5. 如图,在平面内,一组平行线穿过 , 若 , , 则的度数是( ) A、25° B、30° C、35° D、45°6. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、
A、25° B、30° C、35° D、45°6. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、 B、
B、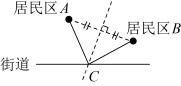 C、
C、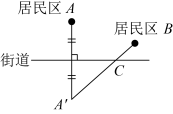 D、
D、 7. 某项目化学习小组的同学在水中掺入酒精,充分混合后,放入冰箱冷冻室.根据实验数据作出混合液温度()随时间()变化而变化的图象.下列说法不正确的是( )
7. 某项目化学习小组的同学在水中掺入酒精,充分混合后,放入冰箱冷冻室.根据实验数据作出混合液温度()随时间()变化而变化的图象.下列说法不正确的是( ) A、在这个变化过程中,自变量是时间,因变量是混合液的温度. B、混合液的温度随着时间的增大而下降. C、当时间为时,混合液的温度为 D、当时,混合液的温度保持不变8. 如图,已知∠DAB=∠CBA,添加下列条件不一定使△ABD与△BAC全等的是( )
A、在这个变化过程中,自变量是时间,因变量是混合液的温度. B、混合液的温度随着时间的增大而下降. C、当时间为时,混合液的温度为 D、当时,混合液的温度保持不变8. 如图,已知∠DAB=∠CBA,添加下列条件不一定使△ABD与△BAC全等的是( ) A、BD=AC B、AD=BC C、∠D=∠C D、∠DBA=∠CAB9. 数形结合是数学解题中常用的思想方法,可以使某些抽象的数学问题直观化、简洁化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材都安排了运用图形面积加以验证.下列图形中能验证的是( )A、
A、BD=AC B、AD=BC C、∠D=∠C D、∠DBA=∠CAB9. 数形结合是数学解题中常用的思想方法,可以使某些抽象的数学问题直观化、简洁化,能够变抽象思维为形象思维,有助于把握数学问题的本质.在学习整式运算乘法公式的过程中,每个公式的推导教材都安排了运用图形面积加以验证.下列图形中能验证的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中,为中线,过点B作于点E,过点C作于点F.在延长线上取一点G,连接 , 使 . 下列结论中正确的个数为( )
10. 如图,在中,为中线,过点B作于点E,过点C作于点F.在延长线上取一点G,连接 , 使 . 下列结论中正确的个数为( )①;②;③;④
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 40°角的余角是.12. 据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约毫升.小明同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小明离开分钟后,水龙头滴出毫升的水,则与之间的函数关系式是 .13. 七巧板起源于我国宋代,后流传于世界各国.在“综合与实践”课堂上,兴趣小组同学用一张正方形纸板依据图1,经过折叠、剪切,制作了如图2所示的七巧板,再拼成如图3所示的作品,最后在作品上随机钉一枚图钉,将其固定在桌面上,则图钉的钉尖恰好落在①区域的概率是 .
 14. 如图,BD平分 , P是上一点,过点P作于点Q, , O是上任意一点,连接 , 则的最小值为 .
14. 如图,BD平分 , P是上一点,过点P作于点Q, , O是上任意一点,连接 , 则的最小值为 . 15. 如图,在中, , , 和关于直线对称,的平分线交于点G,连接 , 当为等腰三角形时,的度数为 .
15. 如图,在中, , , 和关于直线对称,的平分线交于点G,连接 , 当为等腰三角形时,的度数为 .
三、解答题
-
16.(1)、计算: .(2)、化简求值: , 其中 .17. 如图,已知:直线 , 直线分别交、于点、 .
 (1)、实践与操作:作线段的垂直平分线,分别交、于点、 , 交点 . (要求:尺规作图,不写做法,保留作图痕迹)(2)、猜想与证明:试猜想线段和的数量关系,并说明理由.18. 已知 , 求代数式的值.
(1)、实践与操作:作线段的垂直平分线,分别交、于点、 , 交点 . (要求:尺规作图,不写做法,保留作图痕迹)(2)、猜想与证明:试猜想线段和的数量关系,并说明理由.18. 已知 , 求代数式的值.解:
(第一步)
(第二步)
(第三步)
由 , 得 (第四步)
所以,原式 (第五步)
任务:
(1)、该解法运用的主要数学思想是____.A、转化思想 B、数形结合思想 C、公理化思想 D、整体思想(2)、该解答过程在第步开始出现错误,错误的原因是 .(3)、请你借鉴该解题方法,写出此题的正确解答过程.19. 某市林业局积极响应习总书记“青山绿水就是金山银山”的号召,特地考察一种花卉移植的成活率,对本市这种花卉移植成活的情况进行了调查统计,并绘制了如图所示的统计图.
请你根据统计图提供的信息,回答下列问题:
(1)、这种花卉成活的频率稳定在附近,估计成活概率为 . (精确到0.1)(2)、该林业局已经移植这种花卉20000棵.①估计这批花卉成活的棵树;
②根据市政规划共需要成活90000棵这种花卉,估计还需要移植多少棵?
20. 学习《利用三角形全等测距离》后,“开拓”小组同学就“测量河两岸、两点间距离”这一问题,设计了如下方案:如图,在点所在河岸同侧平地上取点和点 . 使点、、在一条直线上,且 , 测得 , , 在的延长线上取一点 , 使 , 这时测得的长就是、两点间的距离.你同意他们的说法吗?请说明理由. 21. “忠义仁勇数关公”,说的就是关羽关圣人.农历四月初八,关公游城,祈福国泰民安,风调雨顺,街头人山人海.管理处工作人员用无人机进行航拍,操控无人机需要根据现场状况调节高度,已知无人机上升或下降的速度相同,无人机的高度h(米)与操控无人机的时间t(分)之间的关系如图中的实线所示,根据图象回答下列问题:
21. “忠义仁勇数关公”,说的就是关羽关圣人.农历四月初八,关公游城,祈福国泰民安,风调雨顺,街头人山人海.管理处工作人员用无人机进行航拍,操控无人机需要根据现场状况调节高度,已知无人机上升或下降的速度相同,无人机的高度h(米)与操控无人机的时间t(分)之间的关系如图中的实线所示,根据图象回答下列问题: (1)、在上升或下降过程中,无人机升降的速度是多少?(2)、图中a、b表示的数分别是a= , b= .(3)、求第14分钟时无人机飞行的高度.22. 阅读与思考
(1)、在上升或下降过程中,无人机升降的速度是多少?(2)、图中a、b表示的数分别是a= , b= .(3)、求第14分钟时无人机飞行的高度.22. 阅读与思考下面是小明同学的数学学习笔记,请您仔细阅读并完成相应的任务:构造全等三角形解决图形与几何问题
在图形与几何的学习中,常常会遇到一些问题无法直接解答,需要添加辅助线才能解决.比如下面的题目中出现了角平分线和垂线段,我们可以通过延长垂线段与三角形的一边相交构造全等三角形,运用全等三角形的性质解决问题.
例:如图1,是内一点,且平分 , , 连接 , 若的面积为10,求的面积.

该问题的解答过程如下:
解:如图2,过点作交延长线于点 , 、交于点 ,

平分 ,
.
,
.
在和中, ,
(依据1)
(依据2), ,
, .
……
(1)、任务一:上述解答过程中的依据1,依据2分别是 , ;(2)、任务二:请将上述解答过程的剩余部分补充完整;(3)、应用:如图3,在中, , , 平分交于点 , 过点作交延长线于点 . 若 , 求的长. 23. 综合与实践
23. 综合与实践
 (1)、问题情境:
(1)、问题情境:如图1,中, , , 点C在直线l上,点A、B在直线l的同侧,过点A作于点D.
如图1,在直线l上取点E,使 . 则与的数量关系是 , 此时、、之间的数量关系是 .
(2)、探究证明:如图2,在直线l上取点F,使 , 猜想与的数量关系,并说明理由(辅助线提示:过点B作于点H)
(3)、拓展延伸:在直线l任取一点P,连接 , 以点P为直角顶点作等腰直角三角形 , 作 于点N,请分别探索在图3,图4中、、之间的数量关系,直接写出答案.