贵州省黔东南州教学资源共建共享实验基地名校2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 要使式子 有意义,则 x 的取值范围是( )A、 B、 C、 D、2. 直线与x轴的交点是( )A、 B、 C、 D、3.
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
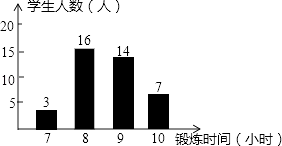 A、16,10.5 B、8,9 C、16,8.5 D、8,8.54. 函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 正方形具有而矩形不一定具有的性质是 ( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、四个角都是直角6. 我国古代数学著作九章算术中记载了一个问题:“今有池方一丈,葭生其中,出水一尺引葭赴岸,适与岸齐问水深几何”丈、尺是长度单位,1丈=10尺其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面水的深度是多少?则水深为( )
A、16,10.5 B、8,9 C、16,8.5 D、8,8.54. 函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 正方形具有而矩形不一定具有的性质是 ( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、四个角都是直角6. 我国古代数学著作九章算术中记载了一个问题:“今有池方一丈,葭生其中,出水一尺引葭赴岸,适与岸齐问水深几何”丈、尺是长度单位,1丈=10尺其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面水的深度是多少?则水深为( ) A、10尺 B、11尺 C、12尺 D、13尺7. 如图,▱ OABC 的顶点 O、A、C 的坐标分别是(0,0),(2,0),(0.5,1),则点 B 的坐 标是( )
A、10尺 B、11尺 C、12尺 D、13尺7. 如图,▱ OABC 的顶点 O、A、C 的坐标分别是(0,0),(2,0),(0.5,1),则点 B 的坐 标是( )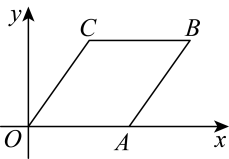 A、(1,2) B、(0.5,2) C、(2.5,1) D、(2,0.5)8. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( )
A、(1,2) B、(0.5,2) C、(2.5,1) D、(2,0.5)8. 某物体在力 的作用下,沿力的方向移动的距离为 ,力对物体所做的功 与 的对应关系如图所示,则下列结论正确的是( ) A、 B、 C、 D、9. 如图,在中,D、E分别是边、的中点,若 , 则( )
A、 B、 C、 D、9. 如图,在中,D、E分别是边、的中点,若 , 则( ) A、3 B、6 C、12 D、2410. 设实数a,b在数轴上对应的位置如图所示,化简 +|a+b|的结果是( )
A、3 B、6 C、12 D、2410. 设实数a,b在数轴上对应的位置如图所示,化简 +|a+b|的结果是( ) A、-2a+b B、2a+b C、-b D、b11. 如图,在平行四边形中, , , , 则该平行四边形的周长为( )
A、-2a+b B、2a+b C、-b D、b11. 如图,在平行四边形中, , , , 则该平行四边形的周长为( ) A、16cm B、 C、 D、20cm12. 如图,甲是第七届国际数学教育大会(简称)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中 , 如果把图乙中的直角三角形继续作下去,那么 , , …,这些线段中长度为正整数有____条.
A、16cm B、 C、 D、20cm12. 如图,甲是第七届国际数学教育大会(简称)的会徽,会徽的主体图案是由如图乙的一连串直角三角形演化而成的,其中 , 如果把图乙中的直角三角形继续作下去,那么 , , …,这些线段中长度为正整数有____条.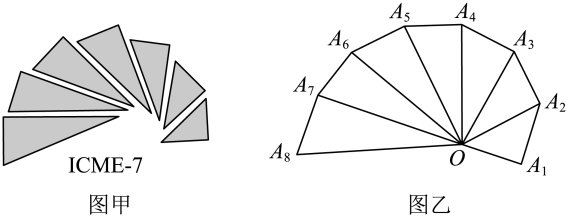 A、25 B、5 C、4 D、6
A、25 B、5 C、4 D、6二、填空题
-
13. 若甲、乙两人射击比赛的成绩(单位:环)如下:
甲:6,7,8,9,10;
乙:7,8,8,8,9.
则甲、乙两人射击成绩比较稳定的是(填甲或乙);
14. 如图,菱形ABCD的两条对角线相交于O , 若AC=6,BD=4,则菱形ABCD的周长是 . 15. 如图,“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形,是我国古代数学的骄傲,巧妙地利用面积关系证明了勾股定理.已知小正方形的面积是1,直角三角形的两直角边分别为a、b且 , 则图中大正方形的边长为 .
15. 如图,“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形,是我国古代数学的骄傲,巧妙地利用面积关系证明了勾股定理.已知小正方形的面积是1,直角三角形的两直角边分别为a、b且 , 则图中大正方形的边长为 . 16. 如图,已知点 , ,直线 经过点 .试探究:直线与线段 有交点时 的变化情况,猜想 的取值范围是.
16. 如图,已知点 , ,直线 经过点 .试探究:直线与线段 有交点时 的变化情况,猜想 的取值范围是.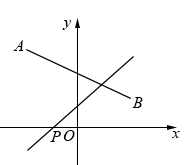
三、/strong>、解答题
-
17. 计算:(1)、(2)、18. 为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下:
收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88
(1)、根据上述数据,将下列表格补充完整.整理、描述数据:
成绩/分
88
89
90
91
95
96
97
98
99
学生人数
2
1
▲
3
2
1
▲
2
1
数据分析:样本数据的平均数、众数和中位数如下表:
平均数
众数
中位数
93
▲
91
(2)、得出结论:根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为分.
(3)、数据应用:根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由.
19. 如图,在的方格纸中,每个小正方形的边长都为1,的三个顶点都在格点上,且 , , . (1)、图中已画出 , 请画出、 , 得到;(2)、判断是不是直角三角形,并说明理由.20. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
(1)、图中已画出 , 请画出、 , 得到;(2)、判断是不是直角三角形,并说明理由.20. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知学校、书店、陈列馆依次在同一条直线上,书店离学校 , 陈列馆离学校 . 李华从学校出发,匀速骑行到达书店;在书店停留后,匀速骑行到达陈列馆;在陈列馆参观学习一段时间,然后回学校;回学校途中,匀速骑行后减速,继续匀速骑行回到学校.给出的图象反映了这个过程中李华离学校的距离与离开学校的时间之间的对应关系.

请根据相关信息,解答下列问题:
(1)、填表:离开学校的时间
1
3
离学校的距离
2
__
12
12
__
(2)、填空:①书店到陈列馆的距离为;
②李华从陈列馆回学校途中,减速前的骑行速度为;
③当李华离学校的距离为时,他离开学校的时间为 .
21. 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n , 利用所学知识就能求出旗杆的长,若米,米,求旗杆的长.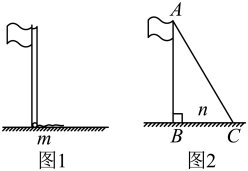 22. 如图,在中,E、F是对角线上的两点(点E在点F左侧),且 .
22. 如图,在中,E、F是对角线上的两点(点E在点F左侧),且 . (1)、求证:四边形是平行四边形;(2)、当 , , 时,求的长.23. 下面是小虎同学做的一道题:
(1)、求证:四边形是平行四边形;(2)、当 , , 时,求的长.23. 下面是小虎同学做的一道题:解:原式…①
…②
…③
(1)、上面的计算过程中最早出现错误的步骤(填序号)是;(2)、请写出正确的计算过程.


