河北省承德市围场县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-04 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{x + 1}$ 在实数范围内有意义，则实数 $x$ 的取值范围是（）

A、 $x \geq - 1$ B、 $x \neq 0$ C、 $x ≥ 1$ D、 $x > 0$

查看试题解析
2. 下列函数中， $y$ 是 $x$ 的正比例函数的是（）

A、 $y = x + 1$ B、 $y = - x^{2}$ C、 $y = \frac{x}{5}$ D、 $y = \frac{5}{x}$

查看试题解析
3. 计算 $\sqrt{5^{2} - 4^{2} - 3^{2}}$ 的结果是（）

A、6 B、0 C、 $\sqrt{6}$ D、4

查看试题解析
4. 如图，在平行四边形 $A B C D$ 中， $∠ A - ∠ B = 50 °$ ，则 $∠ B$ 的度数是（）

A、 $130 °$ B、 $115 °$ C、 $65 °$ D、 $50 °$

查看试题解析
5. 一组数据：0，1，2，2，3，4，若增加一个数据2，则下列统计量中，发生改变的是（）

A、方差 B、众数 C、中位数 D、平均数

查看试题解析
6. 如图，在 $△$ ABC中，∠B= 90°，AB=2，BC=4，四边形ADEC是正方形，则正方形ADEC的面积是（）

A、8 B、16 C、20 D、25

查看试题解析
7. 如图，在 $▱ A B C D$ 中， $E$ 为边 $B C$ 延长线上一点，连结 $A E$ 、 $D E$ ．若△ADE的面积为2，则 $▱ A B C D$ 的面积为（　　）．

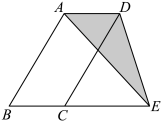A、5 B、4 C、3 D、2

查看试题解析
8. 为了解某校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计．绘制出如下的统计图1和图2，根据相关信息，下列选项正确的是（）

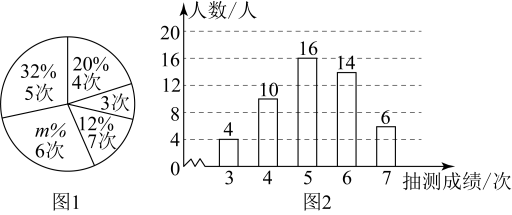A、 $m$ 的值为 $28 %$ B、平均数为5 C、众数为16 D、中位数为5

查看试题解析
9. 共同富裕的要求是：在消除两极分化和贫穷基础上实现普遍富裕．下列有关个人收入的统计量中，最能体现共同富裕要求的是（）

A、平均数小，方差大 B、平均数小，方差小 C、平均数大，方差小 D、平均数大，方差大

查看试题解析
10. 甲、乙两地相距 $300$ 千米，一辆货车和一辆轿车分别从甲地开往乙地 $($ 轿车的平均速度大于货车的平均速度 $)$ ，如图线段 $O A$ 和折线 $B C D$ 分别表示两车离甲地的距离 $y ($ 单位：千米 $)$ 与时间 $x ($ 单位：小时 $)$ 之间的函数关系．则下列说法正确的是（）

A、两车同时到达乙地 B、轿车行驶 $1.3$ 小时时进行了提速 C、货车出发 $3$ 小时后，轿车追上货车 D、两车在前 $80$ 千米的速度相等

查看试题解析
11. 若 $x = \sqrt{5} - 3$ ，则 $\sqrt{x^{2} + 6 x + 9}$ 的值为（）

A、 $\sqrt{5}$ B、 $5$ C、 $\sqrt{5} + 3$ D、 $2$

查看试题解析
12. 两组数据 $- 2$ ， $m$ ， $2 n$ ， 9，12与 $3 m$ ， 7， $n$ 的平均数都是5，若将这两组数据合并为一组新数据，则这组新数据的众数是（）

A、 $- 2$ B、7 C、2 D、9

查看试题解析
13. 如图，点 $A$ ， $B$ 都在格点上，若 $A C = \frac{3}{2} \sqrt{5}$ ，则 $B C$ 的长为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{5}$ C、 $\frac{3 \sqrt{5}}{2}$ D、 $3 \sqrt{5}$

查看试题解析
14. 在凤凰山教育共同体数学学科节中，为展现数学的魅力，M老师组织了一个数学沉浸式互动游戏：随机请A ， B ， C ， D ， E五位同学依次围成一个圆圈，每个人心里先想好一个实数，并把这个数悄悄的告诉相邻的两个人，然后每个人把与自己相邻的两个人告诉自己的数的平均数报出来．若A ， B ， C ， D ， E五位同学报出来的数恰好分别是1，2，3，4，5，则D同学心里想的那个数是（）

A、 $- 3$ B、 $- 4$ C、5 D、9

查看试题解析
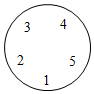15. 如图，四边形ABCD是平行四边形，以点A为圆心，AB的长为半径画弧，交AD于点F；分别以点B，F为圆心，大于 $\frac{1}{2} B F$ 的长为半径画弧，两弧相交于点G：连接AG并延长，交BC于点E．连接BF，若 $A E = 2 \sqrt{10}$ ， $B F = 2 \sqrt{6}$ ，则AB的长为（）

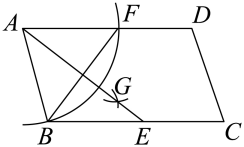A、3 B、4 C、5 D、8

查看试题解析
16. 如图所示，直线y=x+4与两坐标轴分别交于A、B两点，点C是OB的中点，D、E分别是直线AB，y轴上的动点，则△CDE周长的最小值是（）

A、3 $\sqrt{7}$ B、3 $\sqrt{10}$ C、2 $\sqrt{7}$ D、2 $\sqrt{10}$

查看试题解析

二、填空题

17. 如图，直角 $△ A B C$ 中， $A C = 7$ ， $A B = 25$ ，则内部五个小直角三角形的周长和为．

查看试题解析
18. 把一张长方形纸片 $A B C D$ 按如图方式折叠，使点 $A$ 与点 $E$ 重合，点 $C$ 与点 $F$ 重合 $(E$ 、 $F$ 两点均在 $B D$ 上），折痕分别为 $B H$ 、 $D G$ ．若 $A B = 6 c m$ ， $B C = 8 c m$ ，则线段 $F G$ 的长为 $c m$ ．

查看试题解析

19. 全世界大部分国家都采用摄氏温标预报天气，但美国、英国等国家仍然采用华氏温标．某学生查阅资料，得到如下图表中的数据：

摄氏温度值 $x / ℃$	0	10	20	30	40	50
华氏温度值 $y / ^{∘} F$	32	50	68	86	104	122

(1)、分析两种温标计量值的对应关系是否是一次函数？（填“是”或“否”）

(2)、请你根据数据推算

0^{∘} F

时的摄氏温度为

​^{∘} C

查看试题解析

三、解答题

20. 计算：

(1)、 $3 \sqrt{3} + \sqrt{8} - \sqrt{2} + \sqrt{27}$

(2)、 $\frac{1}{2} (\sqrt{3} + \sqrt{5}) - \frac{3}{4} (\sqrt{5} - \sqrt{12})$

(3)、 $(2 \sqrt{5} + \sqrt{6}) (2 \sqrt{5} - \sqrt{6}) - {(\sqrt{5} - \sqrt{6})}^{2}$

查看试题解析
21. 如图所示，在正方形 $A B C D$ 中， $A B = 4$ ，点 $E$ 为边 $B C$ 的中点， $F$ 为 $C D$ 边上一动点，满足 $∠ A E F = 90 °$ ．

(1)、求 $C F$ 的长．

(2)、求 $△ A E F$ 的面积．

查看试题解析
22. 如图，在平行四边形 $A B C D$ 中，点O是 $A D$ 的中点，连接 $B O$ 并延长交 $C D$ 的延长线于点E，连接 $B D$ ， $A E$ ．

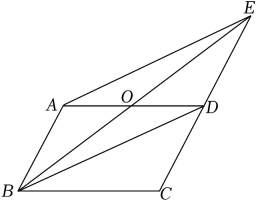(1)、求证：四边形 $A B D E$ 是平行四边形；

(2)、若 $B D = C D$ ，判断四边形 $A B D E$ 的形状，并说明理由．

查看试题解析

23. 某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：经统计发现两班总数相等．

此时有学生建议，可以通过考察数据中的其他信息作为参考．请你回答下列问题：

	1号	2号	3号	4号	5号	总数
甲班	87	100	96	120	97	500
乙班	100	95	110	91	104	500

(1)、求两班比赛成绩的中位数．

(2)、两班比赛成绩数据的方差哪一个小？

(3)、根据以上信息，你认为应该把冠军奖状发给哪一个班级？简述你的理由．

（计算方差的公式： $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ⋯ + {(x_{n} - \bar{x})}^{2}]$ ）

查看试题解析

24. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $A (2 ， 1)$ ，与正比例函数 $y = - 2 x$ 的图象交于点 $D (m ， - 2)$ ，与坐标轴分别交于B、 $C$ 两点．

(1)、求一次函数的解析式；

(2)、求 $C$ 点的坐标；

(3)、求 $△ B O D$ 的面积．

查看试题解析
25. 近年来，某地区坚持经济转型发展的强劲态势，在新能源方面，充分挖掘山脉的风力资源和日照资源优势，加快推进风力发电、光伏发电发展．据统计，2021年风力发电与光伏发电合计发电量为 $28$ 亿度，2022年风力发电与光伏发电合计发电量 $34$ 亿度，已知2022年风力发电量是2021年的 $1.1$ 倍，2022年光伏发电量是2021年的 $1.5$ 倍．

(1)、求该地区2022年风力发电与光伏发电量分别是多少亿度？

(2)、风力发电机组俗称“大风车”，某基地现有 $A 、 B$ 型大风车 $15$ 台，其中 $A$ 型大风车 $a$ 台，且 $B$ 型大风车的数量不低于 $A$ 型大风车的2倍，每台 $A$ 型大风车每年发电量为 $200$ 万度，每台B型大风车每年发电量为 $350$ 万度，若这 $15$ 台大风车每年发电量为 $w$ 万度，请你求出 $w$ 关于 $a$ 的函数关系式，并求出 $w$ 的最小值．

查看试题解析
26. 如图，在四边形ABCD中， $A D ∥ B C$ ， $∠ B = 90 °$ ， $A D = 12 c m$ ， $B C = 15 c m$ ．点P从A点出发以1cm/s的速度向点D运动；同时点Q从点C出发以2cm/s的速度向点B运动．规定运动时间为t秒，当其中一点到达终点时另一点也同时停止运动．

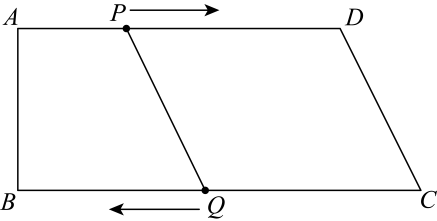(1)、 $A P =$ $c m$ ， $B Q =$ $c m$ （分别用含有 $t$ 的式子表示）；

(2)、当四边形 $P Q C D$ 的面积是四边形 $A B Q P$ 面积的2倍时，求出 $t$ 的值．

(3)、当点 $P$ 、 $Q$ 与四边形 $A B C D$ 的任意两个顶点所形成的四边形是平行四边形时，直接写出 $t$ 的值．

查看试题解析