河北省石家庄市长安区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 如图,“心形”图片盖住的点的坐标可能是( )
 A、 B、 C、 D、2. 如图,学校在琪琪家的( )
A、 B、 C、 D、2. 如图,学校在琪琪家的( )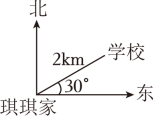 A、北偏东的方向上 B、北偏东的方向上,且距离琪琪家2km C、南偏东的方向上,且距离琪琪家2km D、北偏东的方向上,且距离琪琪家2km3. 函数的自变量x的取值范围是( )A、x≠0 B、x≠1 C、x≥1 D、x≤14. 某校为了解1500名学生周日晚上的睡眠时间,进行了问卷调查,从中抽取了100名学生的睡眠时间,下面说法不正确的是( )A、1500名学生周日晚上的睡眠时间是总体 B、每名学生周日晚上的睡眠时间是个体 C、100名学生是所抽取的一个样本 D、样本的容量是1005. 如图是加油机上的数据显示牌,其中的变量是( )
A、北偏东的方向上 B、北偏东的方向上,且距离琪琪家2km C、南偏东的方向上,且距离琪琪家2km D、北偏东的方向上,且距离琪琪家2km3. 函数的自变量x的取值范围是( )A、x≠0 B、x≠1 C、x≥1 D、x≤14. 某校为了解1500名学生周日晚上的睡眠时间,进行了问卷调查,从中抽取了100名学生的睡眠时间,下面说法不正确的是( )A、1500名学生周日晚上的睡眠时间是总体 B、每名学生周日晚上的睡眠时间是个体 C、100名学生是所抽取的一个样本 D、样本的容量是1005. 如图是加油机上的数据显示牌,其中的变量是( ) A、金额 B、单价 C、油量 D、金额和油量6. 如图,在平面直角坐标系中,一次函数的图象可能是( )
A、金额 B、单价 C、油量 D、金额和油量6. 如图,在平面直角坐标系中,一次函数的图象可能是( )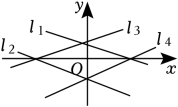 A、直线l1 B、直线l2 C、直线l3 D、直线l47. 点和都在正比例函数 ( , 且k为常数)的图象上,若 , 则k的值可能是( )A、 B、 C、 D、8. 如图,的对角线 , 相交于点O , E是的中点,且 , 则的周长为( )
A、直线l1 B、直线l2 C、直线l3 D、直线l47. 点和都在正比例函数 ( , 且k为常数)的图象上,若 , 则k的值可能是( )A、 B、 C、 D、8. 如图,的对角线 , 相交于点O , E是的中点,且 , 则的周长为( ) A、20 B、16 C、12 D、89. 某市出租车单程收费价格与行驶路程之间的函数关系如图所示,则行驶2千米之后,每行驶1千米增加的钱数为( )
A、20 B、16 C、12 D、89. 某市出租车单程收费价格与行驶路程之间的函数关系如图所示,则行驶2千米之后,每行驶1千米增加的钱数为( ) A、元 B、元 C、元 D、元10. 一张多边形纸片沿如图中的虚线l剪去一部分后,得到一个内角和为1800°的新多边形,则原多边形的边数为( )
A、元 B、元 C、元 D、元10. 一张多边形纸片沿如图中的虚线l剪去一部分后,得到一个内角和为1800°的新多边形,则原多边形的边数为( ) A、13 B、14 C、15 D、1611. 已知在平面直角坐标系中的位置如图所示,将各顶点横坐标不变,纵坐标都乘以后,得到 , 则点的坐标为( )
A、13 B、14 C、15 D、1611. 已知在平面直角坐标系中的位置如图所示,将各顶点横坐标不变,纵坐标都乘以后,得到 , 则点的坐标为( )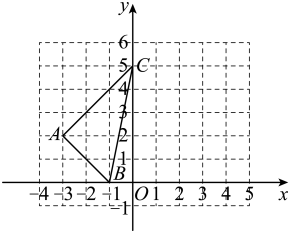 A、 B、 C、 D、12. 如图, , 在此基础上用尺规作出正方形 , 下面说法不正确的是( )
A、 B、 C、 D、12. 如图, , 在此基础上用尺规作出正方形 , 下面说法不正确的是( )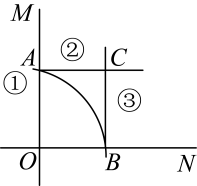 A、弧③的半径长等于弧①的半径长 B、弧②的半径长等于弧①的半径长 C、弧②的半径长小于弧①的半径长 D、弧②的半径长等于弧③的半径长13. 如图,矩形的对角线交于点O , 以点O为原点建立平面直角坐标系,AC所在直线为y轴, , , 则点C的坐标为( )
A、弧③的半径长等于弧①的半径长 B、弧②的半径长等于弧①的半径长 C、弧②的半径长小于弧①的半径长 D、弧②的半径长等于弧③的半径长13. 如图,矩形的对角线交于点O , 以点O为原点建立平面直角坐标系,AC所在直线为y轴, , , 则点C的坐标为( )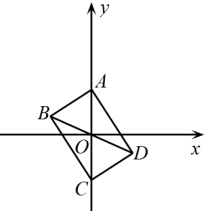 A、 B、 C、 D、14. 如图,点 , , 若N是x轴上使得的值最大的点,则的长为( )
A、 B、 C、 D、14. 如图,点 , , 若N是x轴上使得的值最大的点,则的长为( )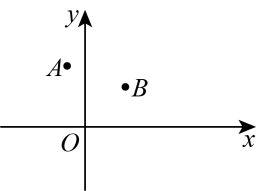 A、 B、 C、8 D、615. 如图,四边形中,为对角线, , , E , F分别是边 , 的中点,则的取值范围是( )
A、 B、 C、8 D、615. 如图,四边形中,为对角线, , , E , F分别是边 , 的中点,则的取值范围是( )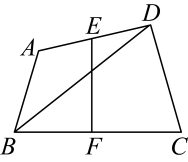 A、 B、 C、 D、16. 如图,在平面直角坐标系中,点 , 点第1次跳动至点 , 第2次跳动至点 , 第3次跳动至点 , 第4次跳动至点…依此规律跳动下去,点第50次跳动至点的坐标是( )
A、 B、 C、 D、16. 如图,在平面直角坐标系中,点 , 点第1次跳动至点 , 第2次跳动至点 , 第3次跳动至点 , 第4次跳动至点…依此规律跳动下去,点第50次跳动至点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 点关于x轴对称的点N的坐标是 .18. 如图,将点绕着原点O逆时针方向旋转得到点B , 则点B的坐标是 .
 19. 某市计划在生态公园内造一片有A , B两种树的混合林,需要购买这两种树苗共500棵,相关信息如表所示.设购买A种树苗x棵,造这片林的总费用为y元.则y(元)与x(棵)之间的函数表达式为 . (总费用=购买树苗的费用+劳务费)
19. 某市计划在生态公园内造一片有A , B两种树的混合林,需要购买这两种树苗共500棵,相关信息如表所示.设购买A种树苗x棵,造这片林的总费用为y元.则y(元)与x(棵)之间的函数表达式为 . (总费用=购买树苗的费用+劳务费)单价(元/棵)
劳务费(元/棵)
A种树苗
20
4
B种树苗
25
5
20. 如图,正方形和正方形的边长分别是2和3,且点A , B , E在同一直线上,M是线段的中点,连结 , , 则的长为 , 的长为 .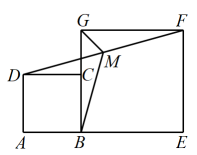
三、解答题
-
21. 已知点 , 根据下列条件分别求出点M的坐标.(1)、点M在y轴上;(2)、点N的坐标为 . 直线轴.22. 周末琪琪骑车郊游,当他骑了一段路时,发现所带饮用水不充足,于是又回到刚经过的某商店,买到水后继续去郊游的目的地,并在1.2小时到达目的地.如图是他本次郊游所用的时间与离家距离的关系示意图,根据图中提供的信息回答下列问题:
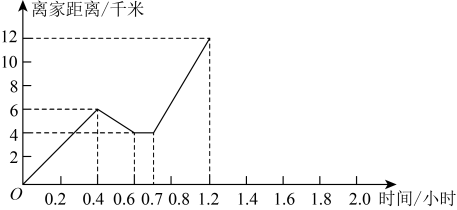 (1)、琪琪家到郊游目的地的路程是 , 琪琪一共骑行了 .(2)、在去目的地的途中,哪个时间段内琪琪的骑车速度最快?最快的速度是多少?(3)、如果琪琪到目的地后,琪琪因急事立刻以20的速度回家,请在图中画出琪琪回家所用时间与离家距离的关系图像.23. 某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
(1)、琪琪家到郊游目的地的路程是 , 琪琪一共骑行了 .(2)、在去目的地的途中,哪个时间段内琪琪的骑车速度最快?最快的速度是多少?(3)、如果琪琪到目的地后,琪琪因急事立刻以20的速度回家,请在图中画出琪琪回家所用时间与离家距离的关系图像.23. 某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下: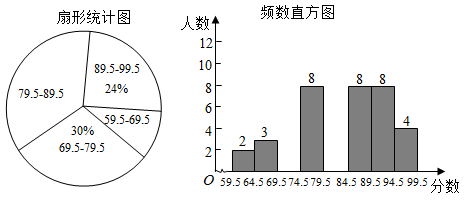 (1)、本次比赛参赛选手共有人,扇形统计图中“”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数直方图;(3)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由.24. 如图,线段两个端点的坐标分别为 , , 直线:( , , 为常数)经过点和 .
(1)、本次比赛参赛选手共有人,扇形统计图中“”这一范围的人数占总参赛人数的百分比为;(2)、补全图2频数直方图;(3)、赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由.24. 如图,线段两个端点的坐标分别为 , , 直线:( , , 为常数)经过点和 . (1)、求直线的解析式;(2)、若将直线向上平移个单位长度,且平移后的直线经过线段的中点,求的值;(3)、直线:经过点 , 且与线段有交点(包含 , 两点),直接写出的取值范围.25.(1)、【探究】如图1,正方形和正方形有公共顶点C.连接求证: .
(1)、求直线的解析式;(2)、若将直线向上平移个单位长度,且平移后的直线经过线段的中点,求的值;(3)、直线:经过点 , 且与线段有交点(包含 , 两点),直接写出的取值范围.25.(1)、【探究】如图1,正方形和正方形有公共顶点C.连接求证: .
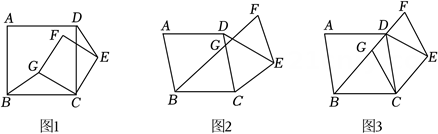 (2)、【变式】如图2,菱形ABCD和菱形有公共顶点C , 且、连接BG,DE。
(2)、【变式】如图2,菱形ABCD和菱形有公共顶点C , 且、连接BG,DE。
是否仍存在结论?若存在,给出证明,若不存在,请说明理由;(3)、如图3,当点G恰好落在对角线上时,点F在延长线上,且 , 若的面积为9,直接写出菱形的面积.