河北省承德市宽城县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 有下列事件:(1)调查长江现有鱼的数量;(2)调查你班每位同学穿鞋的尺码;(3)了解一批电视机的使用寿命;(4)校正某本书上的印刷错误.其中最适合普查的是( )A、(1)(3) B、(1)(4) C、(2)(3) D、(2)(4)2. 函数中自变量x的取值范围为( )A、 B、 C、 D、3. 如图,在▱ABCD中,AC与BD相交于点O,点E是边BC的中点,AB = 4,则OE的长是 ( )
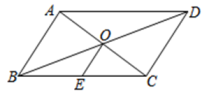 A、2 B、 C、1 D、4. 点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如果一个多边形的内角和等于其外角和的2倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 去年某校有1 500人参加中考,为了了解他们的数学成绩,从中抽取200名考生的数学成绩,其中有60名考生达到优秀,那么该校考生达到优秀的人数约有( )A、400名 B、450名 C、475名 D、500名7. 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A、2 B、 C、1 D、4. 点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如果一个多边形的内角和等于其外角和的2倍,那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形6. 去年某校有1 500人参加中考,为了了解他们的数学成绩,从中抽取200名考生的数学成绩,其中有60名考生达到优秀,那么该校考生达到优秀的人数约有( )A、400名 B、450名 C、475名 D、500名7. 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )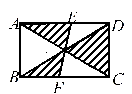 A、6 B、3 C、2 D、18. 如图1,▱ABCD中,AD>AB , ∠ABC为锐角.要用尺规作图的方法在对边AD , BC上分别找点M , N , 使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
A、6 B、3 C、2 D、18. 如图1,▱ABCD中,AD>AB , ∠ABC为锐角.要用尺规作图的方法在对边AD , BC上分别找点M , N , 使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( )
 A、只有乙、丙才是 B、只有甲,丙才是 C、只有甲,乙才是 D、甲、乙、丙都是9. 为了解某市万名学生平均每天读书的时间,请你运用数学的统计知识将统计的主要步骤进行排序:
A、只有乙、丙才是 B、只有甲,丙才是 C、只有甲,乙才是 D、甲、乙、丙都是9. 为了解某市万名学生平均每天读书的时间,请你运用数学的统计知识将统计的主要步骤进行排序:①得出结论,提出建议;
②分析数据;
③从万名学生中随机抽取名学生,调查他们平均每天读书的时间;
④利用统计图表将收集的数据整理和表示.
合理的排序是( )
A、③②④① B、③④②① C、③④①② D、②③④①10. 已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A、经过第一、二、四象限 B、与x轴交于(1,0) C、与y轴交于(0,1) D、y随x的增大而减小11. 已知为直线上的三个点,且 , 则以下判断正确的是( ).A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则12. 如图,l1: y=x+1和l2: y=mx+n相交于P (a , 2),则x+1≥ mx+n解集为( ) A、x>-1 B、x<1 C、x≥1 D、x>a13. 小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系.根据图象,下列说法正确的是( )
A、x>-1 B、x<1 C、x≥1 D、x>a13. 小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系.根据图象,下列说法正确的是( )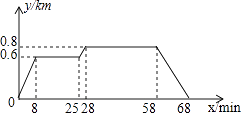 A、小明吃早餐用了25min B、小明读报用了30min C、食堂到图书馆的距离为0.8km D、小明从图书馆回家的速度为0.8km/min14. 如图,已知长方形 中 , ,在边 上取一点 ,将 折叠使点 恰好落在 边上的点 ,则 的长为( )
A、小明吃早餐用了25min B、小明读报用了30min C、食堂到图书馆的距离为0.8km D、小明从图书馆回家的速度为0.8km/min14. 如图,已知长方形 中 , ,在边 上取一点 ,将 折叠使点 恰好落在 边上的点 ,则 的长为( ) A、2cm B、3cm C、4cm D、5cm15. 在同一平面直角坐标系中,函数和的图象可能是( )A、
A、2cm B、3cm C、4cm D、5cm15. 在同一平面直角坐标系中,函数和的图象可能是( )A、 B、
B、 C、
C、 D、
D、 16. 如图,分别沿长方形纸片和正方形纸片 EFGH 的对角线 , 剪开,拼成如图2所示的四边形 , 若中间空白部分四边形恰好是正方形 , 且四边形的面积为50,则正方形的面积是( )
16. 如图,分别沿长方形纸片和正方形纸片 EFGH 的对角线 , 剪开,拼成如图2所示的四边形 , 若中间空白部分四边形恰好是正方形 , 且四边形的面积为50,则正方形的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 点关于原点的对称点的坐标是 .18. 如图所示,在平行四边形ABCD中,∠ABC的平分线交AD于E , 且AE=2,DE=1,则平行四边形ABCD的周长等于 .
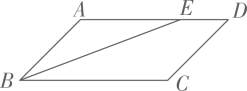 19. 如图,矩形中, , , 动点从点出发沿运动,速度是/秒;点从点出发沿运动,速度是/秒,设它们的运动时间为秒.
19. 如图,矩形中, , , 动点从点出发沿运动,速度是/秒;点从点出发沿运动,速度是/秒,设它们的运动时间为秒. (1)、当时,连接 , ;(2)、若、两点第一次相遇时,秒;第次相遇时,秒.
(1)、当时,连接 , ;(2)、若、两点第一次相遇时,秒;第次相遇时,秒.三、解答题
-
20. 如图,在平行四边形中,E、F分别为、上的点,且 . 根据所给条件提出一个问题,并给与解答.
 21. 如图,点 , 点 .
21. 如图,点 , 点 .
求:
(1)、求和的解析式;(2)、在坐标平面内存在一点C , 使得以O、A、C、B为顶点的四边形为平行四边形,直接写出点C的坐标.22. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D在AB边上一点.过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE . (1)、求证:CE=AD;(2)、当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.23. 为落实“双减”政策,加强“五项管理”,某校建立了作业时长调控制度,以及时采取措施调控作业量,保证初中生每天作业时长控制在90分钟之内.该校就“每天完成作业时长”的情况随机调查了本校部分初中学生,并根据调查结果制成了如下不完整的统计图,其中分组情况是:A组: , B组: , C组: , D组: .
(1)、求证:CE=AD;(2)、当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.23. 为落实“双减”政策,加强“五项管理”,某校建立了作业时长调控制度,以及时采取措施调控作业量,保证初中生每天作业时长控制在90分钟之内.该校就“每天完成作业时长”的情况随机调查了本校部分初中学生,并根据调查结果制成了如下不完整的统计图,其中分组情况是:A组: , B组: , C组: , D组: .
请根据以上信息解答下列问题:
(1)、这次共抽取了名学生进行调查统计;(2)、请补全条形统计图;(3)、扇形统计图中C组所在扇形的圆心角的大小是;(4)、若该约有2000名初中学生,请估计每天完成作业时长在90分钟之内的初中生人数.24. 随着“公园城市”建设的不断推进,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是 , 乙骑行的路程与骑行的时间之间的关系如图所示. (1)、当和时,求出与之间的函数表达式;(2)、根据题意分析,出发时谁在前面?求何时追上?何时超过前面骑行者?25. 如图,已知直线与y轴相较于点 , 直线交y轴于点B , 交直线于点 .
(1)、当和时,求出与之间的函数表达式;(2)、根据题意分析,出发时谁在前面?求何时追上?何时超过前面骑行者?25. 如图,已知直线与y轴相较于点 , 直线交y轴于点B , 交直线于点 . (1)、求直线的解析式;(2)、过动点作x轴的垂线,与直线相交于点M , 与直线相交于点N , 当时,求a的值;(3)、点Q为上一点,若 , 直接写出点Q的坐标.26. 如图,中, , , , 点E从点A出发沿方向以每秒1个单位长的速度向点C匀速运动,同时点F从点B出发沿方向以每秒2个单位长的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点E , F运动的时间是t秒().过点F作于点D , 连接 , , .
(1)、求直线的解析式;(2)、过动点作x轴的垂线,与直线相交于点M , 与直线相交于点N , 当时,求a的值;(3)、点Q为上一点,若 , 直接写出点Q的坐标.26. 如图,中, , , , 点E从点A出发沿方向以每秒1个单位长的速度向点C匀速运动,同时点F从点B出发沿方向以每秒2个单位长的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点E , F运动的时间是t秒().过点F作于点D , 连接 , , . (1)、求证:四边形是平行四边形;(2)、当t为何值时,;(3)、直接写出当t为何值时,为直角三角形?
(1)、求证:四边形是平行四边形;(2)、当t为何值时,;(3)、直接写出当t为何值时,为直角三角形?