北京市燕山区2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-04 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{3^{2}}$ 的结果是（）

A、3 B、 $- 3$ C、 $\pm 3$ D、 $\sqrt{3}$

查看试题解析
2. 如图， $▱ A B C D$ 中， $∠ B = 25 °$ ，则 $∠ A =$ （）

A、 $50 °$ B、 $65 °$ C、 $115 °$ D、 $155 °$

查看试题解析
3. 点 $P (1 ， 3)$ 在正比例函数 $y = k x (k \neq 0)$ 的图象上，则 $k$ 的值为（）

A、 $\frac{1}{3}$ B、2 C、3 D、4

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{8} = \sqrt{10}$ B、 $2 \sqrt{2} - 2 = \sqrt{2}$ C、 $\sqrt{2} \times \sqrt{8} = 4$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
5. 在 $△ A B C$ 中， $∠ A ， ∠ B ， ∠ C$ 的对边分别是a ， b ， c ，下列条件中，不能判定 $△ A B C$ 是直角三角形的是（）

A、 $∠ A + ∠ B = 90 °$ B、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ C、 $a ： b ： c = 3 ： 4 ： 5$ D、 $a = b = 1 ， c = \sqrt{2}$

查看试题解析
6. 某企业参加“科技创新企业百强”评选，创新能力、创新价值、创新影响三项得分分别为8分，9分，7分，若将三项得分依次按5：3：2的比例计算总成绩，则该企业的总成绩为（）

A、8分 B、8.1分 C、8.2分 D、8.3分

查看试题解析
7. 如图，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，如果图中勾 $a = 3$ ，弦 $c = 5$ ，则小正方形的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 下面的三个问题中都有两个变量：①三角形的高一定，三角形的面积y与底边长x；②将泳池中的水匀速放出，直至放完，泳池中的剩余水量y与放水时间x；③一艘观光船沿直线从码头匀速行驶到某景区，观光船与景区间的距离y与行驶时间x ．其中，变量y与变量x之间的函数关系可以用如图所示的图象表示的是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题

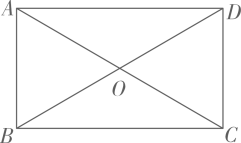
9. 若式子 $\sqrt{x - 5}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 将直线 $y = 3 x$ 向上平移2个单位，得到的直线为.

查看试题解析
11. 已知点 $P (- 2 ， y_{1})$ ， $Q (1 ， y_{2})$ 在一次函数 $y = k x + 1 (k \neq 0)$ 的图象上，且 $y_{1} > y_{2}$ ，则 $k$ 的值可以是（写出一个条件即可）．

查看试题解析
12. 如图，在矩形 $A B C D$ 中对角线 $A C$ ， $B D$ 交于点 $O$ ，请添加一个条件，使矩形 $A B C D$ 是正方形（填一个即可）

查看试题解析
13. 如图，在平面直角坐标系 $x O y$ 中，已知点 $A （ 2 ， 3 ）$ ，以点O为圆心， $O A$ 长为半径画弧，交x轴的正半轴于点B ，则点B的横坐标为．

查看试题解析
14. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ，点 $E$ 为边 $C D$ 的中点，连接 $O E$ ．若 $A C = 2 \sqrt{3}$ ， $B D = 2$ ，则 $O E$ 的长为．

查看试题解析
15. 如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距，某项研究表明，一般情况下人的身高y（单位： $c m$ ）是指距x（单位： $c m$ ）的一次函数，现测得指距x与身高y的几组对应值：

指距x / $c m$

16

18

20

22

身高y/ $c m$

133

151

169

187

小明的身高是 $160 c m$ ，一般情况下，他的指距约是 $c m$ ．

查看试题解析
16. 2023年4月，北京市每日最高气温的统计图如图所示：

根据统计图提供的信息，有下列三个结论：①若按每日最高气温由高到低排序，4月4日排在第30位；②4月7日到4月8日气温上升幅度最大；③若记4月上旬（1日至10日）的最高气温的方差为 $s_{1}^{2}$ ，中旬(11日至20日)的最高气温的方差为 $s_{2}^{2}$ ，下旬（21日至30日）的最高气温的方差为 $s_{3}^{2}$ ，则 $s_{2}^{2} < s_{3}^{2} < s_{1}^{2}$ ．其中所有正确结论的序号是．

查看试题解析

三、解答题

17. 计算： $\sqrt{6} \times \sqrt{50} \div \sqrt{3}$ ．

查看试题解析
18. 计算： ${(\sqrt{2023})}^{0} + | - \sqrt{2} | - \sqrt{18} + (\sqrt{2})^{2}$ ．

查看试题解析
19. 已知 $a = \sqrt{5} + 1$ ，求代数式 $a^{2} - 2 a$ 的值．

查看试题解析
20. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象与两坐标轴分别交于点 $A (- 1 ， 0) ， B (0 ， 3)$ ，求该一次函数的解析式．

查看试题解析

21. 下面是证明平行四边形判定定理“一组对边平行且相等的四边形是平行四边形”的两种思路，选择其中一种，完成证明．

已知：如图，四边形 $A B C D$ 中， $A B ∥ C D$ ， $A B = C D$ ，求证：四边形 $A B C D$ 是平行四边形．

思路一：条件中已有 $A B ∥ C D$ ，只需证明 $B C ∥ A D$ 即可．

证明：如图，连接 $A C$ ．

思路二：条件中已有 $A B = C D$ ，只需证明 $B C = A D$ 即可．

证明：如图，连接 $A C$ ．

查看试题解析

22. 如图，在正方形网格中，每个小正方形网格的边长均为1，点A ， B ， C ， D均在格点上．

(1)、判断 $△ A C D$ 的形状，并说明理由；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，对角线 $A C ， B D$ 交于点O ， $O A = O B$ ．

(1)、求证：四边形 $A B C D$ 是矩形；

(2)、若 $A D = 2 ， ∠ C A B = 30 °$ ，作 $∠ D C B$ 的平分线 $C E$ 交 $A B$ 于点E ，求 $A E$ 的长．

查看试题解析
24. 探究函数性质时，我们经历了列表、描点、连线画出函数的图象，观察分析图象特征，概括函数性质的过程．小腾根据学习函数的经验，对函数 $y_{1} = 2 x$ 与 $y_{2} = - x + 6$ 进行了探究．下面是小腾的探究过程，请补充完整：

(1)、绘制函数图象
①列表：下表是 $x$ 与 $y_{1}$ ， $y_{2}$ 的几组对应值；

          $x$
…
0
1
…
          $y_{1}$
…
0
2
…
          $y_{2}$
…
b
5
…
其中，b=     ▲     ；
②描点、连线：在同一平面直角坐标系xOy中，描出上表中各组数值所对应的点 $(x ， y_{1})$ ， $(x ， y_{2})$ 并画出函数 $y_{1}$ ， $y_{2}$ 的图象．


(2)、结合函数图象，探究函数性质
①函数 $y_{1}$ ， $y_{2}$ 的图象的交点坐标为     ▲  ，则关于x ， y的二元一次方程组 ${\begin{array}{l} y = 2 x ， \\ y = - x + 6 \end{array}$ 的解是     ▲  ；

②过点 $M (m ， 0)$ 作垂直于x轴的直线与函数 $y_{1}$ ， $y_{2}$ 的图象分别交于点P ， Q ，当点P位于点Q下方时， $m$ 的取值范围是     ▲ ．

查看试题解析
25. 为了了解学生对党的二十大精神的学习领会情况，某校团委从七，八年级各随机抽取20名学生进行测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理、描述和分析．下面给出了部分信息：
a ．八年级学生成绩的频数分布直方图如下（数据分为4组： $60 \leq x ＜ 70 ， 70 \leq x ＜ 80 ， 80 \leq x ＜ 90 ， 90 \leq x \leq 100$ ）．

b ．八年级学生成绩在 $80 \leq x ＜ 90$ 这一组的是：
81  83  84  84  84  86  89
c ．七、八年级学生成绩的平均数、中位数、众数如下：

年级
平均数
中位数
众数
七
83.1
88
89
八
83.5
m
84
根据以上信息，回答下列问题：

(1)、写出表中m的值；

(2)、七年级学生小亮和八年级学生小宇的成绩都是86分，这两名学生在本年级成绩排名更靠前的是（填“小亮”或“小宇”），理由是；

(3)、成绩不低于85分的学生可获得优秀奖，假设该校八年级300名学生都参加测试，估计八年级获得优秀奖的学生人数．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，点 $M (a ， m)$ 和点 $N (a + 2 ， n)$ 在一次函数 $y = k x + b (k \neq 0)$ 的图象上．

(1)、若 $a = 0$ ， $m = 4$ ， $n = 2$ ，求该一次函数的解析式；

(2)、已知点 $A (1 ， 2)$ ，将点A向左平移3个单位长度，得到点B ．
①求点B的坐标；
②若 $m - n = 4$ ，一次函数 $y = k x + b (k \neq 0)$ 的图象与线段 $A B$ 有公共点，求 $b$ 的取值范围．

查看试题解析
27. 如图，菱形 $A B C D$ 中， $∠ A B C = 120 °$ ， E为边 $A B$ 上一点，点F在 $D B$ 的延长线上， $E F = E D$ ，作点F关于直线 $A B$ 的对称点G ，连接 $E G$ ．

(1)、依题意补全图形，并证明 $∠ A D E = ∠ F E B$ ；

(2)、用等式表示 $A E ， C G ， D F$ 之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，已知点 $A (0 ， 2)$ ， $B (2 ， 2)$ ，对于直线l和点P ，给出如下定义：若在线段 $A B$ 上存在点Q ，使得点P ， Q关于直线l对称，则称直线l为点P的关联直线，点P是直线l的关联点．

(1)、已知直线 $l_{1}$ ： $y = - x$ ，在点 $P_{1} (- 2 ， 1)$ ， $P_{2} (- 2 ， - 1)$ ， $P_{3} (2 ， 0)$ 中，直线 $l_{1}$ 的关联点是；

(2)、若在x轴上存在点P ，使得点P为直线 $l_{2}$ ： $y = - x + b$ 的关联点，求b的取值范围；

(3)、已知点 $N (n ， - n)$ ，若存在直线 $l_{3}$ ： $y = m x$ 是点N的关联直线，直接写出n的取值范围．

查看试题解析

指距x / $c m$	16	18	20	22
身高y/ $c m$	133	151	169	187

$x$	…	0	1	…
$y_{1}$	…	0	2	…
$y_{2}$	…	b	5	…

年级	平均数	中位数	众数
七	83.1	88	89
八	83.5	m	84