河北省石家庄市栾城区2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 下列点在第三象限的是( )A、(1,1) B、(﹣1,1) C、(﹣1,﹣1) D、(1,﹣1)2. 下列条件不能判定一个四边形是矩形的是( )A、四个内角都相等 B、四条边都相等 C、对角线相等且互相平分 D、对角线相等的平行四边形3. 如图,若菱形的周长 , 则菱形的一边的中点E到对角线交点O的距离为( )
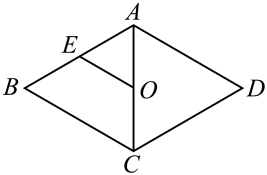 A、 B、 C、 D、4. 若一次函数的图象经过点 , 则的值为( )A、2 B、-2 C、3 D、5. 观察统计图,下列判断错误的是( )
A、 B、 C、 D、4. 若一次函数的图象经过点 , 则的值为( )A、2 B、-2 C、3 D、5. 观察统计图,下列判断错误的是( ) A、甲班男、女生人数相等 B、乙班女生比男生人数多 C、乙班女生比甲班女生人数多 D、无法比较甲、乙两班女生人数谁多谁少6. 如图,是象棋盘的一部分,若“帅”位于点 , “相”位于点上,则“炮”位于点( )上.
A、甲班男、女生人数相等 B、乙班女生比男生人数多 C、乙班女生比甲班女生人数多 D、无法比较甲、乙两班女生人数谁多谁少6. 如图,是象棋盘的一部分,若“帅”位于点 , “相”位于点上,则“炮”位于点( )上.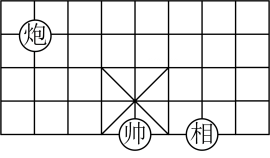 A、 B、 C、 D、7. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、78. 如图,在中, , , 的垂直平分线交于点E,交于点F,连接 , 则的周长是( )
A、 B、 C、 D、7. 若一个多边形的内角和是540°,则该多边形的边数为( )A、4 B、5 C、6 D、78. 如图,在中, , , 的垂直平分线交于点E,交于点F,连接 , 则的周长是( )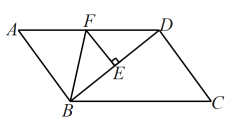 A、6 B、8 C、9 D、109. 实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.下图为表示镭的放射规律的函数图象,据此可计算32mg镭缩减为1mg所用的时间大约是( )
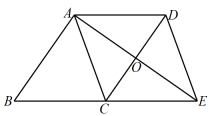
A、6 B、8 C、9 D、109. 实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.下图为表示镭的放射规律的函数图象,据此可计算32mg镭缩减为1mg所用的时间大约是( )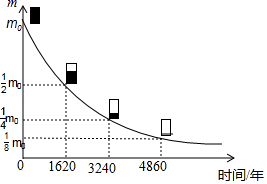 A、4860年 B、6480年 C、8100年 D、9720年10. 如图,四边形的对角线 , 相交于点O, , 且 , 则添加下列一个条件能判定四边形是菱形的是( )
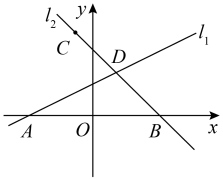
A、4860年 B、6480年 C、8100年 D、9720年10. 如图,四边形的对角线 , 相交于点O, , 且 , 则添加下列一个条件能判定四边形是菱形的是( ) A、 B、 C、 D、11. 已知点 , 在直线的图象上,当时, , 且 , 则在平面直角坐标系中,它的图象大致是( )A、
A、 B、 C、 D、11. 已知点 , 在直线的图象上,当时, , 且 , 则在平面直角坐标系中,它的图象大致是( )A、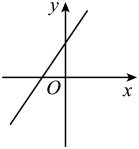 B、
B、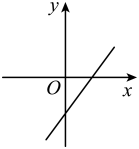 C、
C、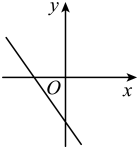 D、
D、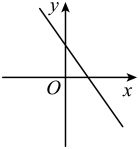 12. 如图,正方形ABCD边长为10,点M在对角线AC上运动,N为DC上一点,DN=2,则DM+ MN长的最小值为( )
12. 如图,正方形ABCD边长为10,点M在对角线AC上运动,N为DC上一点,DN=2,则DM+ MN长的最小值为( )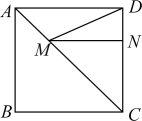 A、8 B、10 C、 D、
A、8 B、10 C、 D、二、填空题
-
13. 函数y= 的自变量x的取值范围是 。14. 如图,在矩形中,对角线相交于点O,的度数为 .
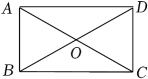 15. 某市中学有初中生3 500人,高中生1500人,为了解学生的视力情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取30人,则初中抽取人数为;16. 某医药研究所研发了一种新药,经临床实验发现,成人按规定剂量服用,每毫升血液中含药量(微克)随时间(小时)而变化的情况如图所示.研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间是小时.
15. 某市中学有初中生3 500人,高中生1500人,为了解学生的视力情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取30人,则初中抽取人数为;16. 某医药研究所研发了一种新药,经临床实验发现,成人按规定剂量服用,每毫升血液中含药量(微克)随时间(小时)而变化的情况如图所示.研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间是小时.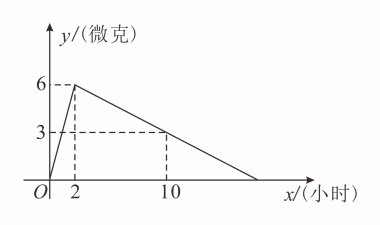 17. 四边形的对角线相交于点 , 且 , , 则 .18. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路s关于行走的时间t和函数图象,则两图象交点P的坐标是.
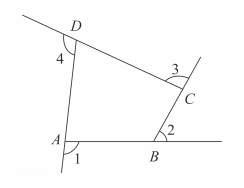
17. 四边形的对角线相交于点 , 且 , , 则 .18. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路s关于行走的时间t和函数图象,则两图象交点P的坐标是.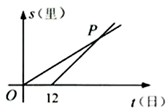 19. 如图是由射线、、、组成的平面图形,则°.
19. 如图是由射线、、、组成的平面图形,则°.
 20. 在平面直角坐标系中,对于任意三个不重合的点 , , 的“矩面积”,给出如下定义:“水平底”指任意两点横坐标差的最大值,“铅垂高”指任意两点纵坐标差的最大值,“矩面积” . 例如: , , 则“水平底” , “铅垂高” , “矩面积” . 若 , , 三点的“矩面积”为 , 则的值为 .
20. 在平面直角坐标系中,对于任意三个不重合的点 , , 的“矩面积”,给出如下定义:“水平底”指任意两点横坐标差的最大值,“铅垂高”指任意两点纵坐标差的最大值,“矩面积” . 例如: , , 则“水平底” , “铅垂高” , “矩面积” . 若 , , 三点的“矩面积”为 , 则的值为 .三、解答题
-
21. 已知,在平面直角坐标系中的位置如图所示.
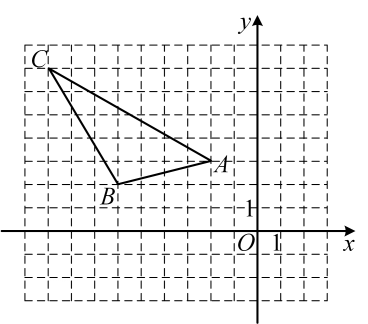 (1)、求的面积.(2)、中任意一点经平移后对应点为 , 将作同样的平移得到 , 请直接写出、、的坐标.22. 如图,等腰直角三角形的直角边与正方形的边都在直线上(点与点重合),且它们都在直线同侧, , 现等腰直角三角形以每秒1个单位的速度从左到右沿直线运动,当点运动到与点重合时运动结束.设运动时间为 , 与正方形重叠部分的面积为 .
(1)、求的面积.(2)、中任意一点经平移后对应点为 , 将作同样的平移得到 , 请直接写出、、的坐标.22. 如图,等腰直角三角形的直角边与正方形的边都在直线上(点与点重合),且它们都在直线同侧, , 现等腰直角三角形以每秒1个单位的速度从左到右沿直线运动,当点运动到与点重合时运动结束.设运动时间为 , 与正方形重叠部分的面积为 .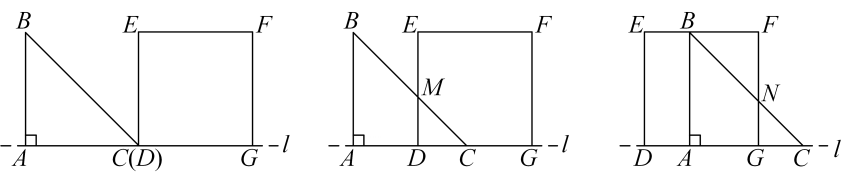 (1)、请直接写出与之间的函数关系式及自变量的取值范围.(2)、当时,求的值.23. 某校七、八、九年级共有1000名学生.学校统计了各年级学生的人数,绘制了图①、图②两幅不完整的统计图.
(1)、请直接写出与之间的函数关系式及自变量的取值范围.(2)、当时,求的值.23. 某校七、八、九年级共有1000名学生.学校统计了各年级学生的人数,绘制了图①、图②两幅不完整的统计图.
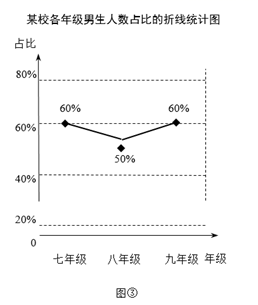
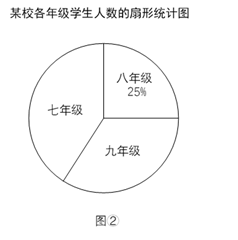 (1)、将图①的条形统计图补充完整.(2)、图②中,表示七年级学生人数的扇形的圆心角度数为°.(3)、学校数学兴趣小组调查了各年级男生的人数,绘制了如图③所示的各年级男生人数占比的折线统计图(年级男生人数占比=该年级男生人数÷该年级总人数×100%).请结合相关信息,绘制一幅适当的统计图,表示各年级男生及女生的人数,并在图中标明相应的数据.
(1)、将图①的条形统计图补充完整.(2)、图②中,表示七年级学生人数的扇形的圆心角度数为°.(3)、学校数学兴趣小组调查了各年级男生的人数,绘制了如图③所示的各年级男生人数占比的折线统计图(年级男生人数占比=该年级男生人数÷该年级总人数×100%).请结合相关信息,绘制一幅适当的统计图,表示各年级男生及女生的人数,并在图中标明相应的数据.