山东省济宁市泗水县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-09-04 类型:期末考试
一、单选题
-
1. 下列算式正确的是( )A、 B、 C、 D、2. 下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=3:4:5 B、∠A:∠B:∠C=3:4:5 C、∠A+∠B=∠C D、a:b:c=1:2:3. 甲、乙,丙、丁4名同学参加跳远测试各10次,他们的平均成绩(单位:m)及其方差如表:
测试者
平均成绩
方差
甲
6.3
0.21
乙
6.0
0.59
丙
5.7
0.12
丁
6.3
0.35
若从其中选出1名成绩好且发挥稳定的同学参加学校运动会,则应选( )
A、甲 B、乙 C、丙 D、丁4. 在平面直角坐标系中,已知点在直线上,则的值为( )A、1 B、 C、2 D、5. 如图,直线上有三个正方形,若 , 的面积分别为和 , 则的面积为( )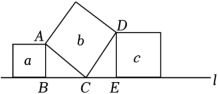 A、9 B、17 C、153 D、1656. 如图,某超市在门口离地高米的墙上,装有一个由传感器控制的门铃 , 如图 , 人只要移至距该门铃米及米以内时,门铃会自动发出语音“欢迎光临”.如图②,一个身高米的顾客走到处,门铃恰好自动响起,则的长为( )
A、9 B、17 C、153 D、1656. 如图,某超市在门口离地高米的墙上,装有一个由传感器控制的门铃 , 如图 , 人只要移至距该门铃米及米以内时,门铃会自动发出语音“欢迎光临”.如图②,一个身高米的顾客走到处,门铃恰好自动响起,则的长为( )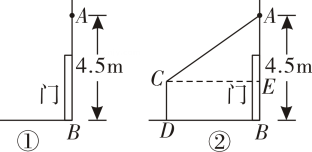 A、6米 B、5米 C、4米 D、3米7. 对一组样本数据进行分析时,列出的方差计算公式为: , 下面结论错误的是( )A、众数是6 B、方差是3.6 C、平均数是8 D、中位数是8.58. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、
A、6米 B、5米 C、4米 D、3米7. 对一组样本数据进行分析时,列出的方差计算公式为: , 下面结论错误的是( )A、众数是6 B、方差是3.6 C、平均数是8 D、中位数是8.58. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、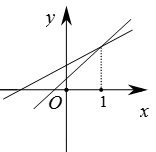 B、
B、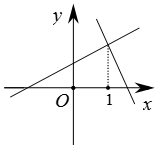 C、
C、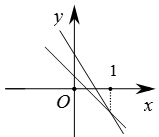 D、
D、 9. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的关系用图象描述大致是( )
9. 如图,在△ABC中,AC=BC,有一动点P从点A出发,沿A→C→B→A匀速运动.则CP的长度s与时间t之间的关系用图象描述大致是( )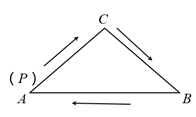 A、
A、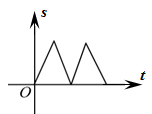 B、
B、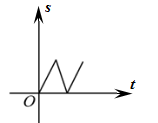 C、
C、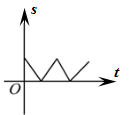 D、
D、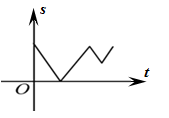 10. 如图,在矩形中, , 点M、N分别在边上,连接 . 若四边形是菱形,则等于( )
10. 如图,在矩形中, , 点M、N分别在边上,连接 . 若四边形是菱形,则等于( )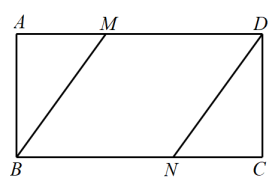 A、 B、 C、 D、11. 已知、两地是一条直路,甲车从地到地,乙车从地到地,两车同时出发,乙先到达目的地,两车之间的距离()与运动时间()的函数关系大致如图所示,下列说法错误的是( )
A、 B、 C、 D、11. 已知、两地是一条直路,甲车从地到地,乙车从地到地,两车同时出发,乙先到达目的地,两车之间的距离()与运动时间()的函数关系大致如图所示,下列说法错误的是( )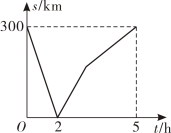 A、两车出发后相遇 B、甲车的速度为/ C、乙的速度为/ D、乙车比甲车提前到达目的地12. 如图,在平面直角坐标系中,点 , , …都在x轴上,点 , , …都在直线上, , , , , …都是等腰直角三角形,且 , 点的横坐标是( )
A、两车出发后相遇 B、甲车的速度为/ C、乙的速度为/ D、乙车比甲车提前到达目的地12. 如图,在平面直角坐标系中,点 , , …都在x轴上,点 , , …都在直线上, , , , , …都是等腰直角三角形,且 , 点的横坐标是( )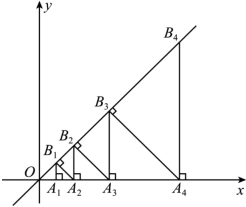 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
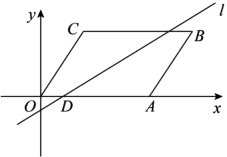
13. 若x , y为实数,且 , 则 .14. 某招聘考试分笔试和面试.其中笔试按、面试按计算平均数作为总成绩.小明笔试成绩为90分.面试成绩为80分,那么小明的总成绩为分.15. 若一次函数的图象经过第一、二、四象限,则m的取值范围是 .16. 如图,在平行四边形中,、 , 若 , 直线经过点并且把平行四边形的面积分成相等的两部分,则直线的解析式是 .
 17. 已知直线: , 将直线向下平移个单位,得到直线 , 设直线与直线的交点为P , 若 , 则m的值为 .18. 如图,在正方形中, , E为对角线上与A , C不重合的一个动点,过点E作于点F , 于点G , 连接 . 下列结论:①;②;③;④的最小值为 . 其中正确结论的序号是 .
17. 已知直线: , 将直线向下平移个单位,得到直线 , 设直线与直线的交点为P , 若 , 则m的值为 .18. 如图,在正方形中, , E为对角线上与A , C不重合的一个动点,过点E作于点F , 于点G , 连接 . 下列结论:①;②;③;④的最小值为 . 其中正确结论的序号是 .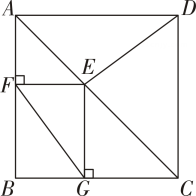
三、解答题
-
19. 计算:(1)、;(2)、已知 , , 求的值.20. 某校开展“远离溺水·珍爱生命”安全知识竞赛,现从该校七、八年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示),共分为五个等级:A . , B . , C . , D . , E . ,
下面给出了部分信息:
七年级15个学生的竞赛成绩:78,83,89,97,98,85,100,94,87,90,93,92,99,95,100
八年级15个学生的竞赛成绩中D等级包含的所有数据为:91,92,94,90,93
七、八年级中各随机抽取15名学生的竞赛成绩统计表
年级
平均数
众数
中位数
方差
七年级
92
a
93
41.7
八年级
92
87
b
50.2
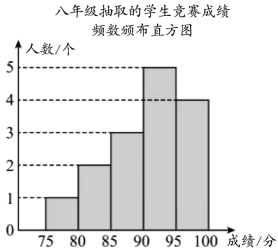 (1)、根据以上信息,可以求出; , ;(2)、根据以上数据,你认为哪个年级的学生的竞赛成绩较好,请从两个不同的角度说明理由.(3)、若规定评分90分及以上为优秀,若参加知识竞赛的七年级有1200人,八年级有1500人,请估算两个年级学生评分为优秀的学生共有多少人.21. 如图,在平面直角坐标系中,直线:分别与轴、轴交于点、 , 且与直线∶交于点 .
(1)、根据以上信息,可以求出; , ;(2)、根据以上数据,你认为哪个年级的学生的竞赛成绩较好,请从两个不同的角度说明理由.(3)、若规定评分90分及以上为优秀,若参加知识竞赛的七年级有1200人,八年级有1500人,请估算两个年级学生评分为优秀的学生共有多少人.21. 如图,在平面直角坐标系中,直线:分别与轴、轴交于点、 , 且与直线∶交于点 .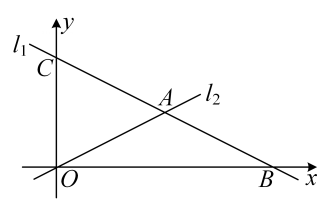 (1)、求出点的坐标;(2)、根据图象,直接写出时x的取值范围是.(3)、若是线段上的点,且的面积为9,求直线的解析式.22. 如图,在矩形中,点E在BC边上,且 , 过点A作交CB的延长线于点F .
(1)、求出点的坐标;(2)、根据图象,直接写出时x的取值范围是.(3)、若是线段上的点,且的面积为9,求直线的解析式.22. 如图,在矩形中,点E在BC边上,且 , 过点A作交CB的延长线于点F .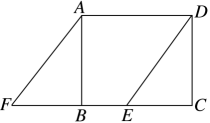 (1)、求证:四边形是菱形;(2)、若 , , 求的长.23. 某运输公司安排大、小两种货车辆恰好一次性将吨的农用物资运往、两村,两种大、小货车的载货能力分别为吨/辆和吨/辆,其运往、两村的运费如下表:
(1)、求证:四边形是菱形;(2)、若 , , 求的长.23. 某运输公司安排大、小两种货车辆恰好一次性将吨的农用物资运往、两村,两种大、小货车的载货能力分别为吨/辆和吨/辆,其运往、两村的运费如下表:车型
村(元/辆)
村(元/辆)
大货车
小货车
(1)、求大、小货车各用了多少辆?(2)、现安排前往村的大、小货车共辆,所运物资不少于吨,其余货车将剩余物资运往村,设大、小两种货车到 , 两村的总运输成本为元,前往村的大货车为辆.写出与之间的函数解析式,当为何值时,调运总费用取得最小值,最少费用是多少?24. 已知点和直线 , 则点P到直线的距离可用公式计算.例如:求点到直线的距离.
解:∵直线 , 其中 , .
∴点到直线的距离为: .
根据以上材料,解答下列问题:
(1)、求点到直线:的距离;(2)、直线:沿y轴向上平移2个单位得到直线 , 求、这两条平行直线之间的距离.25. 如图,在平面直角坐标系中,正方形OABC的边OA , OC分别在x轴,y轴的正半轴上,直线y=2x-6经过线段OA的中点D , 与y轴交于点G , E是线段CG上一点,作点E关于直线DG的对称点F , 连接BE , BF , FG . 设点E的坐标为(0,m).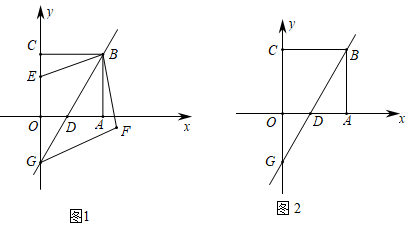 (1)、写出点B的坐标是( , );(2)、当时,求点E的坐标;(3)、在点E的整个运动过程中,
(1)、写出点B的坐标是( , );(2)、当时,求点E的坐标;(3)、在点E的整个运动过程中,①当四边形BEGF为菱形时,求点E的坐标;
②若N为平面内一点,当以B , E , F , N为顶点的四边形为矩形时,m的值为 . (请直接写出答案)