山东省济宁市金乡县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-09-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，正确的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $- \sqrt{3^{2}} = - 3$ C、 $\sqrt{(- 3)^{2}} = \pm 3$ D、 $\sqrt{3^{2}} = \pm 3$

查看试题解析
2. △ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（　　）

A、∠A+∠B=∠C B、∠A：∠B：∠C=1：2：3 C、a²=c²﹣b² D、a：b：c=3：4：6

查看试题解析
3. 某班在学校的合唱比赛中，七个评委给出的得分依次为20，18，22，17，20，20，17，则这组数据的众数与中位数分别是（　　）

A、18，17 B、20，20 C、20，19 D、20，17

查看试题解析
4. 若关于x的一元二次方程为 $a x^{2} + b x + 5 = 0 (a \neq 0)$ 的解是 $x = 1$ ，则 $2021 - a - b$ 的值是（）

A、2016 B、2020 C、2025 D、2026

查看试题解析
5. 如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点连接AF，BF，∠AFB =90°，且AB=8，BC= 14，则EF的长是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 如图，直线 $y_{1} = k x + b$ 经过点A和点B，直线 $y_{2} = 2 x$ 过点A，则不等式 $2 x < k x + b$ 的解集为（）

A、 $x < - 2$ B、 $x < - 1$ C、 $- 2 < x < 0$ D、 $- 1 < x < 0$

查看试题解析
7. 若代数式 $\frac{1}{\sqrt{k - 1}}$ 在实数范围内有意义，则一次函数 $y = (1 - k) x + k - 1$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，菱形ABCD的边长为4，∠DAB＝60°，E为BC的中点，在对角线AC上存在一点P ，使△PBE的周长最小，则△PBE的周长的最小值为（　　）

A、2+2 $\sqrt{3}$ B、4 C、4 $\sqrt{3}$ D、6

查看试题解析
9. 已知a ， b ， c分别是 $R t △ A B C$ 的三条边长，c为斜边长， $∠ C = 90 °$ ，我们把关于x的形如 $y = \frac{a}{c} x + \frac{b}{c}$ 的一次函数称为“勾股一次函数”，若点 $P (- 1 ， \frac{\sqrt{3}}{3})$ 在“勾股一次函数”的图象上，且 $R t △ A B C$ 的面积是4，则c的值是（）

A、 $2 \sqrt{6}$ B、24 C、 $2 \sqrt{3}$ D、12

查看试题解析
10. 如图，在 $△ A B C$ 中，AB＝3，AC＝4，BC＝5， $△ A B D$ ， $△ A C E$ ， $△ B C F$ 都是等边三角形，下列结论中：①AB⊥AC；②四边形AEFD是平行四边形；③∠DFE＝150°；④S_四边形AEFD＝8．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 小明参加“建团百年，我为团旗添光彩”主题演进比赛，其演讲形象、内容、效果三项得分分别是9分，8分，8分．若将三项得分依次按3∶4∶3的比例确定最终成绩，则小明的最终比赛成绩为分．

查看试题解析
12. 如图，∠C＝90°，AB＝12，BC＝3，CD＝4，AD＝13，则四边形ABCD的面积为．

查看试题解析
13. 实数a ， b在数轴上的位置如图所示，化简 $| a + 1 | - \sqrt{{(b - 1)}^{2}} + \sqrt{{(a - b)}^{2}} =$ ．

查看试题解析
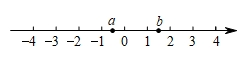14. 元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之.”如图是两匹马行走路s关于行走的时间t和函数图象，则两图象交点P的坐标是.

查看试题解析
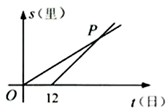15. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F ，连结BF交AC于点M ，连结DE、BO ．若∠COB＝60°，FO＝FC ，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE＝EF；④ $S_{△ A O E} ： S_{△ B C M} = 2 ： 3$ ．其中正确结论的个数是（填写序号）．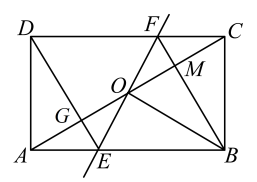

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{12} \times (\sqrt{75} + 3 \sqrt{\frac{1}{3}} - \sqrt{48})$

(2)、解方程 $x^{2} - 4 x - 5 = 0$

查看试题解析
17. 为了解我校学生每天的睡眠时间（单位：小时），随机调查了我校的部分学生，根据调查结果，绘制出如图统计图．若我校共有1000名学生，请根据相关信息，解答下列问题：

(1)、本次接受调查的学生人数为人，扇形统计图中的 $m =$ ；

(2)、请补全条形统计图；

(3)、求所调查的学生每天睡眠时间的方差；

(4)、若睡眠时间超过7小时及以上在白天才能达到良好的学习效果，估计我校学生每天睡眠时间不足的人数．

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中，过点D作 $D E ⊥ A B$ 于点E，点F在边 $C D$ 上， $C F = A E$ ，连接 $A F ， B F$ ．

(1)、求证：四边形 $B F D E$ 是矩形；

(2)、已知 $∠ D A B = 60 °$ ， $A F$ 是 $∠ D A B$ 的平分线，若 $A D = 3$ ，求 $D C$ 的长度．

查看试题解析
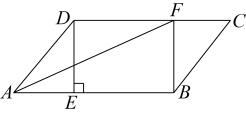19. 在平面直角坐标系中，一次函数 $y = k x + b$ （k ， b都是常数，且 $k \neq 0$ ）的图象经过点 $(1 ， 0)$ 和 $(0 ， - 1)$

(1)、当 $- 1 < x \leq 2$ 时，求y的取值范围．

(2)、已知点 $P (m ， n)$ 在该函数的图象上，且 $m + n = 5$ ，求点P的坐标．

查看试题解析
20. 为振兴乡村经济，弘扬“四敢”精神，某村拟建 $A$ ， $B$ 两类展位供当地的农产品展览和销售.1个 $A$ 类展位的占地面积比1个 $B$ 类展位的占地面积多4平方米，10个 $A$ 类展位和5个 $B$ 类展位的占地面积共280平方米.建 $A$ 类展位每平方米的费用为120元，建 $B$ 类展位每平方米的费用为100元.

(1)、求每个 $A$ ， $B$ 类展位占地面积各为多少平方米；

(2)、该村拟建 $A$ ， $B$ 两类展位共40个，且 $B$ 类展位的数量不大于 $A$ 类展位数量的2倍，求建造这40个展位的最小费用.

查看试题解析
21. 阅读理解：我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形．如图1，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，依次连接各边中点得到中点四边形EFGH．

(1)、判断图1中的中点四边形EFGH的形状，并说明理由；

(2)、当图1中的四边形ABCD的对角线添加条件时，这个中点四边形EFGH是矩形；四边形ABCD的对角线添加条件时，这个中点四边形EFGH是菱形．

(3)、如图2，在四边形ABCD中，点M在AB上且△AMD和△MCB为等边三角形，E、F、G、H分别为AB、BC、CD、AD的中点，试判断四边形EFGH的形状，并证明你的结论．

查看试题解析
22. 如图，在平面直角坐标系中，菱形 $A B C O$ 的顶点 $A (- 6 ， 8)$ ，点 $C$ 在 $x$ 轴正半轴上，对角线 $A C$ 交 $y$ 轴于点 $M$ ，边 $A B$ 交 $y$ 轴于点 $H$ ．动点 $P$ 从点A出发，以2个单位长度/秒的速度沿折线 $A - B - C$ 向终点 $C$ 运动．

(1)、点C的坐标为；点B的坐标为；

(2)、求 $M H$ 的长；

(3)、设动点P的运动时间为t秒连接 $P M$ 、 $B M$ ， $△ P B M$ 的面积为 $S$ ，请用含 $t$ 的式子表示 $S$ ，并说明理由．

查看试题解析