人教版初中数学2023-2024学年八年级上册 11.1与三角形有关的线段检测题
试卷更新日期:2023-09-04 类型:同步测试
一、单选题
-
1. 如果一个三角形的两边长分别是2和5,则第三边可能是( )A、2 B、3 C、5 D、82. 已知△ABC中,AB=6,BC=4,那么边AC的长可能是( )A、11 B、5 C、2 D、13. 教室的一扇窗户打开后,用窗钩可以将其固定,这里所运用的几何原理是( )A、两点之间线段最短 B、三角形的稳定性 C、两点确定一条直线 D、垂线段最短4. 下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,5 B、2,2,4 C、1,2,3 D、2,3,45. AD是 的中线,已知 的周长为25cm,AB比AC长6cm,则 的周长为( )A、19cm B、22cm C、25cm D、31cm6. 以下说法中,正确的个数有( )
( 1 )在坐标轴上的点横坐标、纵坐标都是零(2)点P(2,-3)到x轴的距离为3(3)三角形的三条高都在三角形内部(4)平分三角形内角的射线叫三角形的角平分线
A、1 B、2 C、3 D、47. 有一块三角形的田地ABC,现在要将一半的地种粮食,一半的地种蔬菜,则下列各线中,可把△ABC分成面积相等的两部分的是( )A、一边上的中线 B、一边上的高 C、一角的平分线 D、以上都不对8. 如图,x的值可能为( )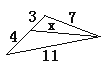 A、10 B、9 C、7 D、69. 若长度分别是a、6、10的三条线段能组成一个三角形,则a的值可以是( )A、16 B、8 C、4 D、210. 如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2 . 其中正确的是( )
A、10 B、9 C、7 D、69. 若长度分别是a、6、10的三条线段能组成一个三角形,则a的值可以是( )A、16 B、8 C、4 D、210. 如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2 . 其中正确的是( )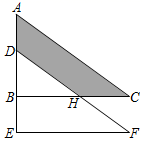 A、①②③④⑤ B、②③④⑤ C、①②③⑤ D、①②④⑤11. 如图,直线与相交于点 , 点在直线上,点在直线上.下列结论不正确的是( )
A、①②③④⑤ B、②③④⑤ C、①②③⑤ D、①②④⑤11. 如图,直线与相交于点 , 点在直线上,点在直线上.下列结论不正确的是( ) A、 B、 C、 D、12. 如图,的三边的长分别是9、12、15.其三条角平分线交于点O , 将分为三个三角形,则等于( )
A、 B、 C、 D、12. 如图,的三边的长分别是9、12、15.其三条角平分线交于点O , 将分为三个三角形,则等于( )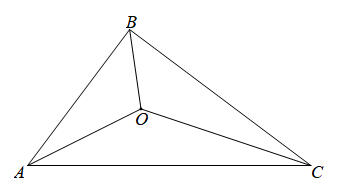 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
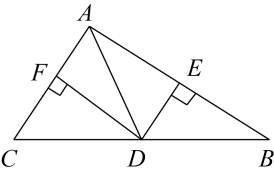
13. 已知三角形的三边分别为a,b,c , 其中a , b满足 ,那么这个三角形的第三边c的取值范围是.14. 已知AD为 的中线, ,且 的周长比 的周长少2cm,则AC= .15. 如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=2.5cm,则的值为.
 16. 如图,△ABC中,点E是BC上的一点,CE=2BE,点D是AC中点,若S△ABC=12,则S△ADF﹣S△BEF= .
16. 如图,△ABC中,点E是BC上的一点,CE=2BE,点D是AC中点,若S△ABC=12,则S△ADF﹣S△BEF= .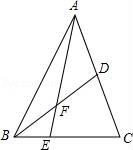 17. 如图,△ABC的面积为18,BD=2DC,AE=2EC,那么阴影部分的面积是。
17. 如图,△ABC的面积为18,BD=2DC,AE=2EC,那么阴影部分的面积是。
三、计算题
-
18. 已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.19. 已知 的三边长分别为 , , ,化简 .
四、解答题
-
20. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
 21. 如图所示,在平面直角坐标系中,已知点A(-5,0),B(-3,0),C(-1,2),求出△ABC的面积.
21. 如图所示,在平面直角坐标系中,已知点A(-5,0),B(-3,0),C(-1,2),求出△ABC的面积.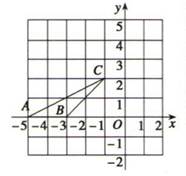 22. 如图,ABCD是凸四边形,AB=2,BC=4,CD=7,求线段AD的取值范围.
22. 如图,ABCD是凸四边形,AB=2,BC=4,CD=7,求线段AD的取值范围.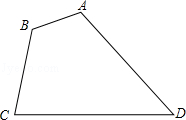
五、综合题