2023年浙教版数学八年级上册第四章 图形与坐标 单元测试(B卷)
试卷更新日期:2023-09-03 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 在一次“寻宝”游戏中,寻宝人已经找到两个标志点和 , 并且知道藏宝地点的坐标是 , 则藏宝处应为图中的( )
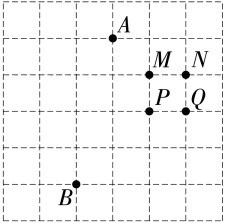 A、点 B、点 C、点 D、点2. 下图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是( )
A、点 B、点 C、点 D、点2. 下图是利用平面直角坐标系画出的首钢园中部分场馆建筑的分布图,若这个坐标系分别以正东、正北方向为 轴、 轴的正方向,表示群明湖的点的坐标为 ,表示冰壶馆的点的坐标为 ,则表示下列场馆建筑的点的坐标正确的是( ) A、滑雪大跳台 B、五一剧场 C、冬奥组委会 D、全民畅读艺术书店3. 将的三个顶点的纵坐标不变,横坐标均乘以后得到 , 则( ).A、与关于x轴对称 B、与关于y轴对称 C、与关于原点对称 D、向x轴的负方向平移了一个单位4. 在平面直角坐标系中,若点在第二象限,则的取值范围在数轴上表示正确的是( )A、
A、滑雪大跳台 B、五一剧场 C、冬奥组委会 D、全民畅读艺术书店3. 将的三个顶点的纵坐标不变,横坐标均乘以后得到 , 则( ).A、与关于x轴对称 B、与关于y轴对称 C、与关于原点对称 D、向x轴的负方向平移了一个单位4. 在平面直角坐标系中,若点在第二象限,则的取值范围在数轴上表示正确的是( )A、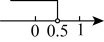 B、
B、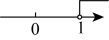 C、
C、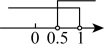 D、
D、 5. 已知在平面直角坐标系中, , , , , 则下列结论正确的是( )A、 B、 C、 D、6. 若点M(x,y)的坐标满足x+y=0,则点M位于( )A、第二象限 B、第一、三象限的夹角平分线上 C、第四象限 D、第二、四象限的夹角平分线上7. 如图,经过一定的平移得到 , 如果上的点的坐标为 , 那么这个点在上的对应点的坐标为( )
5. 已知在平面直角坐标系中, , , , , 则下列结论正确的是( )A、 B、 C、 D、6. 若点M(x,y)的坐标满足x+y=0,则点M位于( )A、第二象限 B、第一、三象限的夹角平分线上 C、第四象限 D、第二、四象限的夹角平分线上7. 如图,经过一定的平移得到 , 如果上的点的坐标为 , 那么这个点在上的对应点的坐标为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( ) A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)9. 如图,在平面直角坐标系中,存在动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2021次运动后,点P的坐标是( )
A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)9. 如图,在平面直角坐标系中,存在动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2021次运动后,点P的坐标是( ) A、(2022,1) B、(2021,0) C、(2021,1) D、(2021,2)10. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )
A、(2022,1) B、(2021,0) C、(2021,1) D、(2021,2)10. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )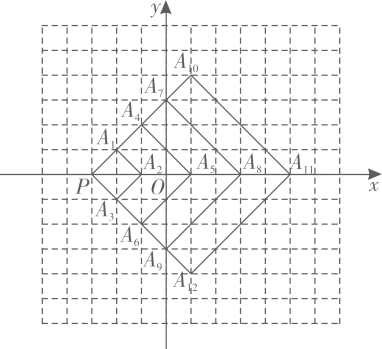 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 如图是一台雷达探测相关目标得到的结果,若记图中目标A的位置为(2,),目标B 的位置为(4,),现有一个目标C的位置为(3,),且与目标B的距离为5,则目标C的位置为 .
 12. 如图,有一个英文单词,它的各个字母的位置依次是 , , , , , 所对应的字母,如对应的字母是K,则这个英文单词为 .
12. 如图,有一个英文单词,它的各个字母的位置依次是 , , , , , 所对应的字母,如对应的字母是K,则这个英文单词为 . 13. 在平面直角坐标系xOy中,点A(﹣4,0),B(2,0)在x轴上,若点P到两坐标轴的距离相等,且∠APO=∠BPO , 则点P的坐标为 .14. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日迫及之.”意思是:现有良马每天行走240里,驽马每天行走150里,驽马先走12天,问良马几天可以追上驽马?两匹马行走路程S(里)与行走时间t(日)的函数关系如图所示,则图中交点P的坐标是 .
13. 在平面直角坐标系xOy中,点A(﹣4,0),B(2,0)在x轴上,若点P到两坐标轴的距离相等,且∠APO=∠BPO , 则点P的坐标为 .14. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日迫及之.”意思是:现有良马每天行走240里,驽马每天行走150里,驽马先走12天,问良马几天可以追上驽马?两匹马行走路程S(里)与行走时间t(日)的函数关系如图所示,则图中交点P的坐标是 .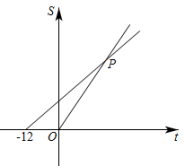 15. 第一象限内有两点 , 将线段平移使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .16. 在平面直角坐标系中,对于平面内任一点 , 若规定以下两种变换:
15. 第一象限内有两点 , 将线段平移使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .16. 在平面直角坐标系中,对于平面内任一点 , 若规定以下两种变换:⑴ . 如:;
⑵ . 如:;
按照以上变换有: , 那么等于 .
三、解答题(共8题,共66分)
-
17. 如图是某地火车站及周围的简单平面图.(每个小正方形的边长代表1千米.)
 (1)、请以火车站所在的位置为坐标原点,建立平面直角坐标系,并表示出体育场A、超市B市场C、文化宫D的坐标.(2)、在这个坐标平面内,连接OA,若∠AOB的度数大约为53°,请利用所给数据描述体育场相对于火车站的位置.(3)、要想用第(2)问的方法描述文化宫在火车站的什么位置,需要测量哪些数据?18. 如图, 的三个顶点在边长为1的正方形网格中,已知 , , .
(1)、请以火车站所在的位置为坐标原点,建立平面直角坐标系,并表示出体育场A、超市B市场C、文化宫D的坐标.(2)、在这个坐标平面内,连接OA,若∠AOB的度数大约为53°,请利用所给数据描述体育场相对于火车站的位置.(3)、要想用第(2)问的方法描述文化宫在火车站的什么位置,需要测量哪些数据?18. 如图, 的三个顶点在边长为1的正方形网格中,已知 , , .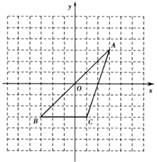 (1)、画出 关于y轴对称的 ,且点A的对应点为 ,点B的对应点为 ,点C的对应点为 ;(2)、在(1)的条件下, , , 的坐标分别是 , , ;(3)、请直接写出第四象限内以 为边且与 全等的三角形的第三个顶点(不与C重合)的坐标,这点的坐标为.19. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
(1)、画出 关于y轴对称的 ,且点A的对应点为 ,点B的对应点为 ,点C的对应点为 ;(2)、在(1)的条件下, , , 的坐标分别是 , , ;(3)、请直接写出第四象限内以 为边且与 全等的三角形的第三个顶点(不与C重合)的坐标,这点的坐标为.19. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2). (1)、在图中作出△ABC关于x轴的对称图形△A1B1C1;(2)、请直接写出点C关于y轴的对称点C'的坐标:;(3)、△ABC的面积=;(4)、在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.20. 如图,是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
(1)、在图中作出△ABC关于x轴的对称图形△A1B1C1;(2)、请直接写出点C关于y轴的对称点C'的坐标:;(3)、△ABC的面积=;(4)、在y轴上找一点P,使得△PAC周长最小,并求出△PAC周长的最小值.20. 如图,是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作: (1)、请在网格中建立直角坐标系,使A点坐标为 , B点坐标为;(2)、在网格上,找一格点C,使点C与线段AB组成等腰三角形,这样的C点共有个;(3)、在(1)(2)的前提下,在第四象限中,当是以AB为底的等腰三角形,且腰长为无理数时,的周长是 , 面积是.21. 在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的三个顶点的坐标分别为 , ,
(1)、请在网格中建立直角坐标系,使A点坐标为 , B点坐标为;(2)、在网格上,找一格点C,使点C与线段AB组成等腰三角形,这样的C点共有个;(3)、在(1)(2)的前提下,在第四象限中,当是以AB为底的等腰三角形,且腰长为无理数时,的周长是 , 面积是.21. 在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的三个顶点的坐标分别为 , , (1)、请在图中的网格平面内建立平面直角坐标系,并将画出来.(2)、在图中找一点D,使 , , 并将点D标记出来.(3)、在x轴上找一点P,使的值最小,请直接写出点P的坐标.(4)、在y轴上是否存在点Q,使得 , 如果存在,求出点Q的坐标,如果不存在,说明理由.22. 操作与探究
(1)、请在图中的网格平面内建立平面直角坐标系,并将画出来.(2)、在图中找一点D,使 , , 并将点D标记出来.(3)、在x轴上找一点P,使的值最小,请直接写出点P的坐标.(4)、在y轴上是否存在点Q,使得 , 如果存在,求出点Q的坐标,如果不存在,说明理由.22. 操作与探究 (1)、对数轴上的点P进行如下操作:先把点P表示的数乘以 ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
(1)、对数轴上的点P进行如下操作:先把点P表示的数乘以 ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.如图1,点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.
若点A表示的数是﹣3,点A′表示的数是;若点B′表示的数是2,点B表示的数是;
已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是.
(2)、对平面直角坐标系中的每个点P进行如下操作:先把点P的横、纵坐标都乘以同一种实数a,将得到的点先向右平移b个单位,再向上平移4b个单位,得到点P的对应点P′.如图2,正方形ABCD在平面直角坐标系中,对正方形ABCD及其内部的点进行上述操作后得到正方形A′B′C′D′及其内部的点,其中点A,B,C,D的对应点分别为A′,B′,C′,D′.
①若已知A(﹣3,0)、A′(﹣1,2)、C(5,4),求点C′的坐标;
②如果正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
23.(1)、如图,我们把杜甫《绝句》整齐排列放在平面直角坐标系中:①“两”、“岭”和“船”的坐标依次是:、和;
②将第2行与第3行对调,再将第3列与第7列对调,“雪”的坐标变换为;
③“泊”开始的坐标是(2,1),使它的坐标变换到(5,3),应该将第行与第行对调,同时将第列与第列对调.
 (2)、如图,△A1B1C1 三个顶点的坐标分别为 A1(1,1),B1(4,2),C1(3,4).请画出△ABC , 使△ABC 与△A1B1C1 关于y轴对称,并写出点A , B , C的坐标。
(2)、如图,△A1B1C1 三个顶点的坐标分别为 A1(1,1),B1(4,2),C1(3,4).请画出△ABC , 使△ABC 与△A1B1C1 关于y轴对称,并写出点A , B , C的坐标。 24. 如图①,在矩形OACB中,点A在x轴正半轴上,点B在y轴正半轴上,点C在第一象限,OA=8,OB=6
24. 如图①,在矩形OACB中,点A在x轴正半轴上,点B在y轴正半轴上,点C在第一象限,OA=8,OB=6 (1)、直接写出点C的坐标:;(2)、如图②,点G在BC边上,连接AG,将△ACG沿AG折叠,点C恰好与线段AB上一点重合,求线段CG的长度;
(1)、直接写出点C的坐标:;(2)、如图②,点G在BC边上,连接AG,将△ACG沿AG折叠,点C恰好与线段AB上一点重合,求线段CG的长度; (3)、如图③,P是直线y=2x-6上一点,PD⊥PB交线段AC于D.若P在第一象限,且PB=PD,试求符合条件的所有点P的坐标.
(3)、如图③,P是直线y=2x-6上一点,PD⊥PB交线段AC于D.若P在第一象限,且PB=PD,试求符合条件的所有点P的坐标.