2023年浙教版数学八年级上册4.3坐标平面内图形的轴对称和平移同步测试（培优版）

试卷更新日期：2023-09-03 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图， $△ A B C$ 沿着直线 $B C$ 向右平移得到 $△ D E F$ ， $A C$ 与 $D E$ 相交于点G，则以下四个结论：① $B E = C F$ ；② $A B ∥ D E$ ；③ $D G = E G$ ；④ $S_{四边形 A B E G} = S_{四边形 D G C F}$ ，其中正确的是（　　）

A、①②③ B、①②④ C、②④ D、①③④

查看试题解析
2. 四盏灯笼的位置如图，已知A，B，C，D的坐标分别是 $(- 4 ， 3)$ ， $(- 3 ， 3)$ ， $(- 2 ， 3)$ ， $(2 ， 3)$ ，平移其中一盏灯，使得y轴两边的灯笼对称，下列说法正确的是（）

A、平移点A到 $(4 ， 3)$ B、平移点B到 $(4 ， 3)$ C、平移点C到 $(4 ， 3)$ D、平移点C到 $(3 ， 3)$

查看试题解析
3. 如图，x轴是△AOB的对称轴，y轴是△BOC的对称轴，点A的坐标为(1，2)，则点C的坐标为（）

A、( -1，-2) B、( 1，-2) C、( -1，2) D、( -2，-1)

查看试题解析
4. 在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， …若点A₁的坐标为（2，4），点A₂₀₂₁的坐标为（）

A、（3，﹣1） B、（﹣2，﹣2） C、（﹣3，3） D、（2，4 ）

查看试题解析
5. 如图，在平面直角坐标系中，AB∥EG∥x轴，BC∥DE∥HG∥AP∥y轴，点D、C、P、H在x轴上，A（1，2），B（﹣1，2），D（﹣3，0），E（﹣3，﹣2），G（3，﹣2），把一条长为2022个单位长度且没有弹性的细线（细线的粗细忽略不计）的一端固定在点A处，并按A→B→C→D→E→F→G→H→P→A…的规律紧绕在图形“凸”的边上，则细线另一端所在位置的点的坐标是（）

A、（﹣1，2） B、（﹣1，1） C、（0，1） D、（0，2）

查看试题解析
6. 已知点A（3，4），B（ -1，-2），将线段AB平移后得到线段CD，其中点4平移到点C，点B平移到点D，平移后点C、点D恰好都落在坐标轴上，则点C的坐标是（）

A、（0，6） B、（4，0） C、（6，0）或（0，4） D、（0，6）或（4 ，0）

查看试题解析
7. 如图，正方形ABCD的顶点A(1，1)，B(3， 1)，规定把正方形ABCD“先沿x轴进行翻折，再向左平称1个单位”为一次变换，这样连续经过2021次变换后，正方形ABCD的顶点C的坐标为（）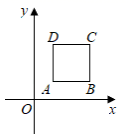

A、(-2018，3) B、(-2018，-3) C、(-2019，3) D、(-2019， -3)

查看试题解析
8. 已知点E（x₀ ， y_o），点F（x₂.y₂），点M（x₁ ， y₁）是线段EF的中点，则x₁＝ $\frac{x_{0} + x_{2}}{2}$ ，y₁＝ $\frac{y_{0} + y_{2}}{2}$ .在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P₁（即P，A，P₁三点共线，且PA＝P₁A），P₁关于点B的对称点P₂ ， P₂关于点C的对称点P₃ ， …按此规律继续以A，B，C三点为对称点重复前面的操作.依次得到点P₄ ， P₅ ， P₆…，则点P₂₀₂₀的坐标是（　　）

A、（4，0） B、（﹣2，2） C、（2，﹣4） D、（﹣4，2）

查看试题解析
9. 如图，点A₁（1，1），点A₁向上平移1个单位，再向右平移2个单位，得到点A₂；点A₂向上平移2个单位，再向右平移4个单位，得到点A₃；点A₃向上平移4个单位，再向右平移8个单位，得到点A₄ ， ……，按这个规律平移得到点A_n ，则点A_n的横坐标为（　　）

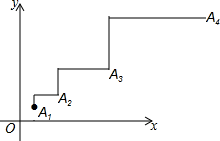A、2ⁿ B、2^n-1 C、2ⁿ-1 D、2ⁿ+1

查看试题解析
10. 在平面直角坐标系中，正方形ABCD的顶点分别为A（1，1）.B（1，﹣1）.C（﹣1，﹣1）.D（﹣1，1），y轴上有一点P（0，2）．作点P关于点A的对称点P₁ ，作P₁关于点B的对称点P₂ ，作点P₂关于点C的对称点P₃ ，作P₃关于点D的对称点P₄ ，作点P₄关于点A的对称点P₅ ，作P₅关于点B的对称点P₆┅，按如此操作下去，则点P₂₀₁₁的坐标为（）

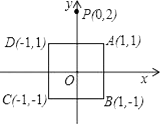A、（0，2） B、（2，0） C、（0，﹣2） D、（﹣2，0）

查看试题解析

二、填空题（第15题4分，其余题每题3分）

11. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（m，n），则经过第2021次变换后所得的A点坐标是．

查看试题解析
12. 如图：在直角坐标系中，设一动点自 $P_{0} (1 ， 0)$ 处向上运动1个单位至 $P_{1} (1 ， 1)$ ，然后向左运动2个单位至 $P_{2}$ 处，再向下运动3个单位至 $P_{3}$ 处，再向右运动4个单位至 $P_{4}$ 处，再向上运动5个单位至 $P_{5}$ 处，如此继续运动下去．设 $P_{n} (x_{n} ， y_{n})$ ， $n = 1$ ， 2，3…，则 $x_{1} + x_{2} + x_{3} + \cdot \cdot \cdot + x_{2020} + x_{2021} + x_{2022} =$ ．

查看试题解析
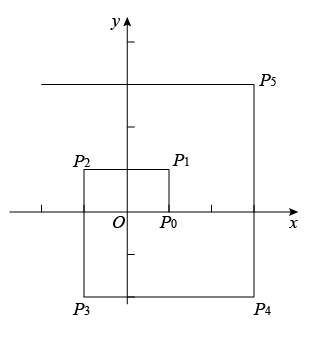13. 如图第一象限内有两点 $P (m - 4 ， n)$ ， $Q (m ， n - 3)$ ，将线段 $P Q$ 平移，使点 $P$ 、 $Q$ 分别落在两条坐标轴上，则点 $P$ 平移后的对应点的坐标是.

查看试题解析
14. 如图，是 $8 \times 8$ 的“密码”图，利用平移对应文字，“今天考试”解密为“祝你成功”，用此“钥匙”解密“遇水架桥”的词语是．

查看试题解析
15. 如图，在平面直角坐标系xOy中，对正方形ABCD及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一种实数a，将得到的点先向右平移m个单位，再向上平移n个单位（m $>$ 0，n $>$ 0），得到正方形A′B′C′D′及其内部的点，其中点A，B的对应点分别为A′，B′，则a＝， m＝， n＝．若正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合，则点F的坐标为．

查看试题解析
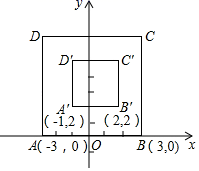16. 对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5）.已知点A的坐标为（1，0）.如图，点M是直线l上的一点，点A关于点M的对称点为点B，点B关于直线l的对称点为点C.若点B由点A经n次斜平移后得到，且点C的坐标为（7，6），则点B的坐标为及n的值为.

查看试题解析
17. 如图，在平面直角坐标系中，已知A（0，4）、B（6，0）、C（0，﹣10），平移线段AB至线段CD，点Q在四边形ACDB内，满足S_△QOC：S_△QOB＝5：2，S_△QCD＝S_△QBD ，则点Q的坐标为．

查看试题解析

三、解答题（共8题，共68分）

18. 如果△ABC关于x轴进行轴对称变换后，得到△A₁B₁C₁ ，而△A₁B₁C₁关于y轴进行轴对称变换后，得到△A₂B₂C₂ ，若△ABC三个顶点坐标分别为A（-2，3）、B（-4，2）、C（-1，0），请你分别写出△A₁B₁C₁与△A₂B₂C₂各顶点坐标．

查看试题解析
19. 如图，已知图中 $A$ 点和 $B$ 点的坐标分别为 $(2 ， - 4)$ 和 $(- 2 ， 2)$ .

(1)、请在图1中画出坐标轴建立适当的直角坐标系；

(2)、写出点 $C$ 的坐标为；

(3)、连接 $A B$ 、 $B C$ 和 $C A$ 得 $Δ A B C$ ，在 $y$ 轴有点 $D$ 满足 $S_{Δ A B C} = S_{Δ D B C}$ ，则点 $D$ 的坐标为， $S_{Δ D B C} =$ 个平方单位；

(4)、已知第一象限内有两点 $P (3 ， n + 2)$ ， $Q (6 ， n)$ 平移线段 $P Q$ 使点 $P$ 、 $Q$ 分别落在两条坐标轴上，则点 $P$ 平移后的对应点的坐标是.

查看试题解析
20. 如图，在正方形网络中，每个小方格的的边长为1个单位长度， $Δ A B C$ 的顶点A，B的坐标分别为(0，5)，(-2，2).

(1)、请在图中建立平面直角坐标系，并写出点 $C$ 的坐标：.

(2)、平移 $Δ A B C$ ，使点 $C$ 移动到点 $F (7 ， - 4)$ ，画出平移后的 $Δ D E F$ ，其中点D与点A对应，点E与点B对应.

(3)、求 $Δ A B C$ 的面积.

(4)、在坐标轴上是否存在点 $P$ ，使 $Δ P O C$ 的面积与 $Δ A B C$ 的面积相等，若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析
21. 在平面直角坐标系中，点O为坐标原点，点B在x轴正半轴上，且OB=2．

(1)、若点A在y轴正半轴上，∠OAB=30°且△ABO和△ABO′关于直线AB对称，求此时点O′的横坐标．

(2)、已知，点M（m，0）、N（0，n）（2＜n＜4），将点B向上平移2个单位长度后得到点B′，若∠MB′N=90°，且mn= $\frac{15}{7}$ ，求m²+n²的值．

查看试题解析
22. 已知点P（2a﹣12，1﹣a）位于第三象限，点Q（x，y）位于第二象限且是由点P向上平移一定单位长度得到的．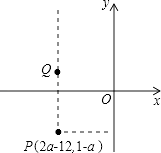

(1)、若点P的纵坐标为﹣3，试求出a的值；

(2)、在（1）题的条件下，试求出符合条件的一个点Q的坐标；

(3)、若点P的横、纵坐标都是整数，试求出a的值以及线段PQ长度的取值范围．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中， $A (a ， - a)$ ， $B (b ， c)$ ，且 $a ， b ， c$ 满足 ${\begin{cases} a + 2 b + 3 c = 12 ， \\ 3 a - 2 b + c = 4 . \end{cases}$

(1)、若 $a$ 没有平方根，判断点 $A$ 位于第几象限，并说明理由；

(2)、若 $P$ 为直线 $A B$ 上一点，且 $O P$ 的最小值为3，求点 $B$ 的坐标；

(3)、已知坐标系内有两点 $C (- b ， c - 4)$ ， $D (c ， 4 - b)$ ， $M (m ， n)$ 为线段 $A C$ 上一点，将点 $M$ 平移至点 $N (m + h ， n + k)$ .若点 $N$ 在线段 $B D$ 上，记 $h + k$ 的最小值为 $s$ ，最大值为 $t$ ，当 $- 4 \leq a \leq - 1$ 时，请判断 $s + t$ 是否为定值？若是，求出该定值，若不是，试讨论 $s + t$ 的取值范围.

查看试题解析
24. 在平面直角坐标系中，点A（m，n）满足n＝ $\sqrt{m - 4} - \sqrt{4 - m} + \sqrt{m}$ .

(1)、直接写出点A的坐标；

(2)、如图1，将线段OA沿y轴向下平移a个单位后得到线段BC（点O与点B对应），过点C作CD⊥y轴于点D，若4OD＝3BD，求a的值；

(3)、如图2，点E（0，5）在y轴上，连接AE，将线段OA沿y轴向上平移3个单位后得到线段FG（点O与点F对应），FG交AE于点P，y轴上是否存在点Q，使S_△_APQ＝6，若存在，请求Q点的坐标；若不存在，请说明理由.

查看试题解析
25. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2m-6，0），B（4，0），C（-1，2），点A、B分别在原点两侧，且A、B两点间的距离等于6个单位长度．

(1)、求m的值；

(2)、在x轴上是否存在点M，使△COM面积＝ $\frac{1}{3}$ △ABC面积，若存在，请求出点M的坐标；若不存在，请说明理由．

(3)、如图2，把线段AB向上平移2个单位得到线段EF，连接AE，BF，EF交y轴于点G，过点C作CD⊥AB于点D，将长方形GOBF和长方形AECD分别以每秒1个单位长度和每秒2个单位长度的速度向右平移，同时，动点M从点A出发，以每秒1个单位长度的速度沿折线AECDA运动，当长方形GOBF与长方形AECD重叠面积为1时，求此时点M的坐标．

查看试题解析

2023年浙教版数学八年级上册4.3坐标平面内图形的轴对称和平移 同步测试（培优版）

一、选择题（每题3分，共30分）

二、填空题（第15题4分，其余题每题3分）

三、解答题（共8题，共68分）

2023年浙教版数学八年级上册4.3坐标平面内图形的轴对称和平移同步测试（培优版）