2019-2023高考数学真题分类汇编27 算法框图与推理证明、反证法
试卷更新日期:2023-09-02 类型:二轮复习
一、选择题
-
1. 执行如图所示的程序框图,输出的s值为( )
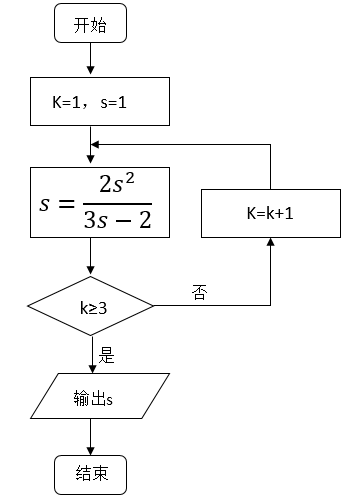 A、1 B、2 C、3 D、42. 执行下边的程序框图,则输出的( )
A、1 B、2 C、3 D、42. 执行下边的程序框图,则输出的( ) A、21 B、34 C、55 D、893. 执行下面的程序框遇,输出的( )
A、21 B、34 C、55 D、893. 执行下面的程序框遇,输出的( )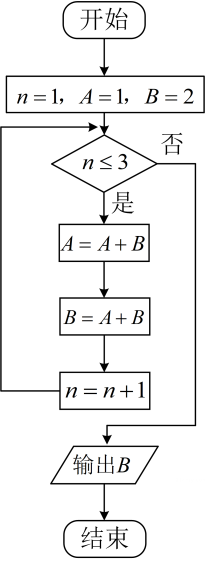 A、21 B、34 C、55 D、894. 执行下边的程序框图,输出的 ( )
A、21 B、34 C、55 D、894. 执行下边的程序框图,输出的 ( ) A、3 B、4 C、5 D、65. 如图,将钢琴上的12个键依次记为a1 , a2 , …,a12.设1≤i<j<k≤12.若k–j=3且j–i=4,则称ai , aj , ak为原位大三和弦;若k–j=4且j–i=3,则称ai , aj , ak为原位小三和弦.用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为( )
A、3 B、4 C、5 D、65. 如图,将钢琴上的12个键依次记为a1 , a2 , …,a12.设1≤i<j<k≤12.若k–j=3且j–i=4,则称ai , aj , ak为原位大三和弦;若k–j=4且j–i=3,则称ai , aj , ak为原位小三和弦.用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为( ) A、5 B、8 C、10 D、156. 执行右面的程序框图,若输入的k=0,a=0,则输出的k为( )
A、5 B、8 C、10 D、156. 执行右面的程序框图,若输入的k=0,a=0,则输出的k为( )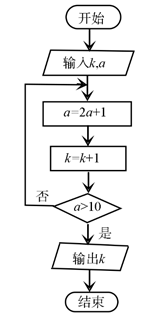 A、2 B、3 C、4 D、57. 0-1周期序列在通信技术中有着重要应用.若序列 满足 ,且存在正整数m,使得 成立,则称其为0-1周期序列,并称满足 的最小正整数m为这个序列的周期.对于周期为m的0-1序列 , 是描述其性质的重要指标,下列周期为5的0-1序列中,满足 的序列是( )A、 B、 C、 D、8. 基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0 , T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )A、1.2天 B、1.8天 C、2.5天 D、3.5天9. 2020年3月14日是全球首个国际圆周率日( Day).历史上,求圆周率 的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为 的近似值.按照阿尔·卡西的方法, 的近似值的表达式是( ).A、 B、 C、 D、10. 阅读下边的程序框图,运行相应的程序,输出 的值为( )
A、2 B、3 C、4 D、57. 0-1周期序列在通信技术中有着重要应用.若序列 满足 ,且存在正整数m,使得 成立,则称其为0-1周期序列,并称满足 的最小正整数m为这个序列的周期.对于周期为m的0-1序列 , 是描述其性质的重要指标,下列周期为5的0-1序列中,满足 的序列是( )A、 B、 C、 D、8. 基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0 , T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( )A、1.2天 B、1.8天 C、2.5天 D、3.5天9. 2020年3月14日是全球首个国际圆周率日( Day).历史上,求圆周率 的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为 的近似值.按照阿尔·卡西的方法, 的近似值的表达式是( ).A、 B、 C、 D、10. 阅读下边的程序框图,运行相应的程序,输出 的值为( ) A、5 B、8 C、24 D、2911. 执行下边的程序框图,如果输入的 为0.01,则输出 的值等于( )
A、5 B、8 C、24 D、2911. 执行下边的程序框图,如果输入的 为0.01,则输出 的值等于( ) A、 B、 C、 D、12. 在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测。
A、 B、 C、 D、12. 在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测。甲:我的成绩比乙高。
乙:丙的成绩比我和甲的都高。
丙:我的成绩比乙高。
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为( )
A、甲、乙、丙 B、乙、甲、丙 C、丙、乙、甲 D、甲、丙、乙13. 下图是求 的程序框图,图中空白框中应填入( ) A、A= B、A=2+ C、A= D、A=1+
A、A= B、A=2+ C、A= D、A=1+二、填空题
