2019-2023高考数学真题分类汇编26 概率和统计综合-在线组卷题库

2. 改革开放以来，人们的支付方式发生了巨大转变.近年来，移动支付已成为主要支付方式之一.为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额

支付方式

不大于2000元

大于2000元

仅使用A

27人

3人

仅使用B

24人

1人

（I）估计该校学生中上个月A，B两种支付方式都使用的人数；

（II）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；

（III）已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中，随机抽查1人，发现他本月的支付金额大于2000元，结合（II）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由.

查看试题解析

3. 为探究某药物对小鼠的生长抑制作用，将40只小鼠均分为两组，分别为对照组（不加药物）和实验组（加药物）．

(1)、设其中两只小鼠中对照组小鼠数目为

X

，求

X

的分布列和数学期望；

(2)、测得40只小鼠体重如下（单位：g）：（已按从小到大排好）

对照组：17.3 18.4 20.1 20.4 21.5 23.2 24.6 24.8 25.0 25.4

26.1 26.3 26.4 26.5 26.8 27.0 27.4 27.5 27.6 28.3

实验组：5.4 6.6 6.8 6.9 7.8 8.2 9.4 10.0 10.4 11.2

14.4 17.3 19.2 20.2 23.6 23.8 24.5 25.1 25.2 26.0

（i）求40只小鼠体重的中位数m，并完成下面2×2列联表：

	<m	>m	合计
对照组
实验组
合计

（ii）根据2×2列联表，能否有95%的把握认为药物对小鼠生长有抑制作用．

参考数据：

$k_{0}$	0.10	0.05	0.010
$P (k^{2} \geq k_{0})$	2.706	3.841	6.635

查看试题解析

4. 在某地区进行流行病调查，随机调查了100名某种疾病患者的年龄，得到如下的样本数据频率分布直方图．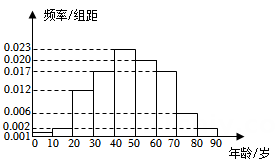

(1)、估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值作代表）；

(2)、估计该地区一人患这种疾病年龄在区间

[20 ， 70)

的概率；

(3)、已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间

[40 ， 50)

的人口占该地区总人口的16%，从该地区任选一人，若此人年龄位于区间

[40 ， 50)

，求此人患该种疾病的概率．（样本数据中的患者年龄位于各区间的频率作为患者年龄位于该区间的概率，精确到0.0001）

查看试题解析

5. 甲、乙两城之间的长途客车均由A和B两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：

	准点班次数	未准点班次数
A	240	20
B	210	30

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

$P (K^{2} ⩾ k)$	0.100	0.050	0.010
$k$	2.706	3.841	6.635

(1)、根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；

(2)、能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？

查看试题解析

6. 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系，在己患该疾病的病例中随机调查了100例(称为病例组)，同时在未患该疾病的人群中随机调查了100人(称为对照组)，得到如下数据：

	不够良好	良好
病例组	40	60
对照组	10	90

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$

P(K² ≥ k)	0.050	0.010	0.001
K	3.841	6.635	10.828

(1)、能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异?

(2)、从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”，

\frac{P (B ∣ A)}{P (\bar{B} ∣ A)}

与

\frac{P (B ∣ \bar{A})}{P (\bar{B} ∣ \bar{A})}

的比值是卫生习惯不够良好对患该

疾病风险程度的一项度量指标，记该指标为R.

(i)证明： $R = \frac{P (A ∣ B)}{P (\bar{A} ∣ B)} \cdot \frac{P (\bar{A} ∣ \bar{B})}{P (A ∣ \bar{B})} ；$

(ii)利用该调查数据，给出 $P (A | B) ， P (A ∣ \bar{B})$ 的估计值，并利用(i)的结果给出R的估计值.

查看试题解析

7. 某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：

锻炼人次空气质量等级	[0，200]	(200，400]	(400，600]
1（优）	2	16	25
2（良）	5	10	12
3（轻度污染）	6	7	8
4（中度污染）	7	2	0

(1)、分别估计该市一天的空气质量等级为1，2，3，4的概率；

(2)、求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；

(3)、若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

	人次≤400	人次>400
空气质量好
空气质量不好

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

P(K²≥k)	0.050	0.010	0.001
k	3.841	6.635	10.828

查看试题解析

8. 某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：

锻炼人次空气质量等级	[0，200]	(200，400]	(400，600]
1（优）	2	16	25
2（良）	5	10	12
3（轻度污染）	6	7	8
4（中度污染）	7	2	0

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

P(K²≥k)	0.050	0.010	0.001
k	3.841	6.635	10.828

(1)、分别估计该市一天的空气质量等级为1，2，3，4的概率；

(2)、求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；

(3)、若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？

	人次≤400	人次>400
空气质量好
空气质量不好

查看试题解析

9. 为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的

PM 2.5

和

{SO}_{2}

浓度（单位：

μ {g/m}^{3}

），得下表：

${SO}_{2}$ $PM 2.5$	$[0, 50]$	$(50, 150]$	$(150, 475]$

$[0, 35]$	32	18	4
$(35, 75]$	6	8	12
$(75, 115]$	3	7	10

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

$P (K^{2} \geq k)$	0.050 0.010 0.001
$k$	3.841 6.635 10.828

(1)、估计事件“该市一天空气中

PM 2.5

浓度不超过75，且

{SO}_{2}

浓度不超过150”的概率；

(2)、根据所给数据，完成下面的

2 \times 2

列联表：

${SO}_{2}$

$PM 2.5$

$[0, 150]$

$(150, 475]$

$[0, 75]$

$(75, 115]$

(3)、根据（2）中的列联表，判断是否有

99 %

的把握认为该市一天空气中

PM 2.5

浓度与

{SO}_{2}

浓度有关？

查看试题解析

10. 2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有

72 ， 108 ， 120

人，现采用分层抽样的方法，从该单位上述员工中抽取25人调查专项附加扣除的享受情况.

（Ⅰ）应从老、中、青员工中分别抽取多少人？

（Ⅱ）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为 $A ， B ， C ， D ， E ， F$ .享受情况如右表，其中“ ”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.

员工项目	A	B	C	D	E	F
子女教育	○	○	×	○	×	○
继续教育	×	×	○	×	○	○
大病医疗	×	×	×	○	×	×
住房贷款利息	○	○	×	×	○	○
住房租金	×	×	○	×	×	×
赡养老人	○	○	×	×	×	○

（i）试用所给字母列举出所有可能的抽取结果；

（ii）设 $M$ 为事件“抽取的2人享受的专项附加扣除至少有一项相同”，求事件 $M$ 发生的概率.

查看试题解析

11. 改革开放以来，人们的支付方式发生了巨大转变。近年来，移动支付已成为主要支付方式之一。为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：

支付金额（元）

支付方式

（0，1000]

（1000，2000]

大于2000

仅使用A

18人

9人

3人

仅使用B

10人

14人

1人

（I）从全校学生中随机抽取1人，估计该学生上个月A，B两种支付方式都使用的概率；

（II）从样本仅使用A和仅使用B的学生中各随机抽取1人，以X表示这2人中上个月支付金额大于1000元的人数，求X的分布列和数学期望；

（III）已知上个月样本学生的支付方式在本月没有变化。现从样本仅使用A的学生中，随机抽查3人，发现他们本月的支付金额都大于2000元，根据抽查结果，能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化？说明理由.

查看试题解析

12. 某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：

	满意	不满意
男顾客	40	10
女顾客	30	20

(1)、分别估计男、女顾客对该商场服务满意的概率；

(2)、能否有95%的把握认为男、女顾客对该商场服务的评价有差异？

附：K²⁼ $\frac{m {(a d - b c)}^{2}}{（ a+b) (c + d) (a + c) (b + d)}$

P（K²≧k）	0.050 0.010 0.001
k	3.841 6.635 10.828

查看试题解析

2019-2023高考数学真题分类汇编26 概率和统计综合

一、选择题

二、解答题