2019-2023高考数学真题分类汇编21 空间向量与立体几何(1)
试卷更新日期:2023-09-02 类型:二轮复习
一、选择题
-
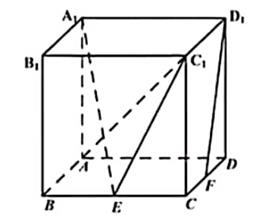
1. 在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )A、 B、 C、 D、2. 坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若 , 且等腰梯形所在的平面、等腰三角形所在的平面与平面的夹角的正切值均为 , 则该五面体的所有棱长之和为( )
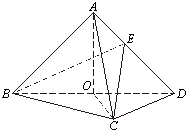
 A、 B、 C、 D、3. 已知为等腰直角三角形,AB为斜边,为等边三角形,若二面角为 , 则直线CD与平面ABC所成角的正切值为( )A、 B、 C、 D、4. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( )
A、 B、 C、 D、3. 已知为等腰直角三角形,AB为斜边,为等边三角形,若二面角为 , 则直线CD与平面ABC所成角的正切值为( )A、 B、 C、 D、4. 如图,已知正三棱柱 ,E,F分别是棱 上的点.记 与 所成的角为 , 与平面 所成的角为 ,二面角 的平面角为 ,则( ) A、 B、 C、 D、5. 在长方体 中,已知 与平面 和平面 所成的角均为 ,则( )A、 B、AB与平面 所成的角为 C、 D、 与平面 所成的角为6. 在正方体 中,E,F分别为 的中点,则( )A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面
A、 B、 C、 D、5. 在长方体 中,已知 与平面 和平面 所成的角均为 ,则( )A、 B、AB与平面 所成的角为 C、 D、 与平面 所成的角为6. 在正方体 中,E,F分别为 的中点,则( )A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面二、多项选择题
-
7. 已知正方体 则( )A、直线 与 所成的角为 B、直线 与 所成的角为 C、直线 与平面 所成的角为 D、直线 与平面ABCD所成的角为
三、解答题
-
8. 如图,在三棱锥中,平面 , .
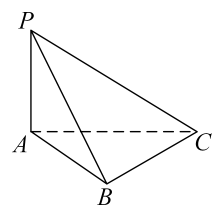 (1)、求证:平面PAB;(2)、求二面角的大小.9. 如图,在三棱柱中,平面 .
(1)、求证:平面PAB;(2)、求二面角的大小.9. 如图,在三棱柱中,平面 . (1)、证明:平面平面;(2)、设 , 求四棱锥的高.10. 三棱台中,若面 , 分别是中点.
(1)、证明:平面平面;(2)、设 , 求四棱锥的高.10. 三棱台中,若面 , 分别是中点. (1)、求证://平面;(2)、求平面与平面所成夹角的余弦值;(3)、求点到平面的距离.11. 如图,在三棱锥中, , , , , BP,AP,BC的中点分别为D,E,O, , 点F在AC上,.
(1)、求证://平面;(2)、求平面与平面所成夹角的余弦值;(3)、求点到平面的距离.11. 如图,在三棱锥中, , , , , BP,AP,BC的中点分别为D,E,O, , 点F在AC上,.
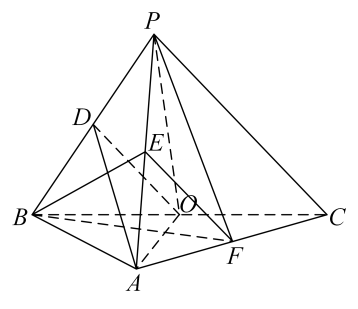 (1)、证明:平面;(2)、证明:平面平面BEF;(3)、求二面角的正弦值.12. 已知直四棱柱.
(1)、证明:平面;(2)、证明:平面平面BEF;(3)、求二面角的正弦值.12. 已知直四棱柱. (1)、求证:面;(2)、若直四棱柱的体积为36,求二面角的大小.13. 如图,三棱锥中,60°,E为BC中点.
(1)、求证:面;(2)、若直四棱柱的体积为36,求二面角的大小.13. 如图,三棱锥中,60°,E为BC中点.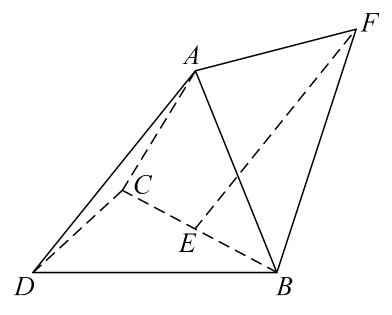 (1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值.14. 直三棱柱中, , D为的中点,E为的中点,F为的中点.
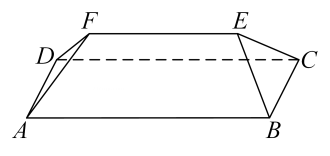
(1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值.14. 直三棱柱中, , D为的中点,E为的中点,F为的中点. (1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、求平面与平面所成二面角的余弦值.15. 如图,已知 和 都是直角梯形, , , , , , ,二面角 的平面角为 .设M,N分别为 的中点.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值;(3)、求平面与平面所成二面角的余弦值.15. 如图,已知 和 都是直角梯形, , , , , , ,二面角 的平面角为 .设M,N分别为 的中点.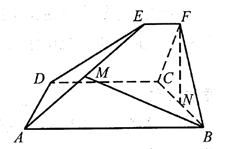
(Ⅰ)证明: ;
(Ⅱ)求直线 与平面 所成角的正弦值.
16. 如图, 是三棱锥 的高, , ,E是 的中点.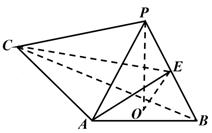 (1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.17. 在四棱锥 中, 底面 .
(1)、求证: 平面 ;(2)、若 , , ,求二面角 的正弦值.17. 在四棱锥 中, 底面 .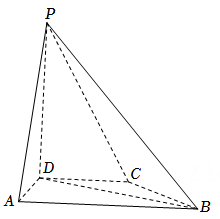 (1)、证明: ;(2)、求PD与平面 所成的角的正弦值.18. 如图,四面体 中, ,E为 的中点.
(1)、证明: ;(2)、求PD与平面 所成的角的正弦值.18. 如图,四面体 中, ,E为 的中点. (1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.19. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.
(1)、证明:平面 平面 ;(2)、设 ,点F在 上,当 的面积最小时,求 与平面 所成的角的正弦值.19. 如图,在三棱柱 中,侧面 为正方形,平面 平面 , , 分别为 , 的中点.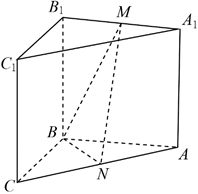
(I)求证: 平面 ;
(II)再从条件①、条件②这两个条件中选择一个作为已知,求
直线 与平面 所成角的正弦值。
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分。
20. 如图,直三棱柱 的体积为4, '的面积为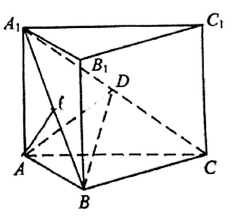 (1)、求A到平面 的距离;(2)、设D为 的中点, 平面 平面 求二面角 的正弦值.21. 在四棱锥 中,底面 是正方形,若 .
(1)、求A到平面 的距离;(2)、设D为 的中点, 平面 平面 求二面角 的正弦值.21. 在四棱锥 中,底面 是正方形,若 . (1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.22. 已知正方体 ,点 为 中点,直线 交平面 于点 .
(1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.22. 已知正方体 ,点 为 中点,直线 交平面 于点 .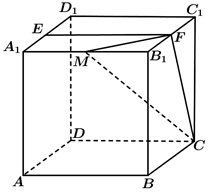 (1)、证明:点 为 的中点;(2)、若点 为棱 上一点,且二面角 的余弦值为 ,求 的值.23. 如图,在四棱锥 中,底面 是平行四边形, ,M , N分别为 的中点, .
(1)、证明:点 为 的中点;(2)、若点 为棱 上一点,且二面角 的余弦值为 ,求 的值.23. 如图,在四棱锥 中,底面 是平行四边形, ,M , N分别为 的中点, .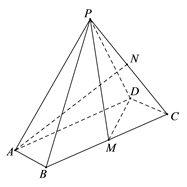 (1)、证明: ;(2)、求直线 与平面 所成角的正弦值.24. 已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
(1)、证明: ;(2)、求直线 与平面 所成角的正弦值.24. 已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形,AB= BC = 2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
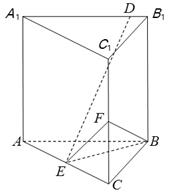 (1)、 证明:BF⊥DE;(2)、当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?25. 如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM,
(1)、 证明:BF⊥DE;(2)、当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?25. 如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM, (1)、求BC;(2)、求二面角A-PM-B的正弦值。
(1)、求BC;(2)、求二面角A-PM-B的正弦值。
-