2019-2023高考数学真题分类汇编20 棱柱、棱锥、棱台、旋转体的体积面积距离

试卷更新日期：2023-09-02 类型：二轮复习

进入出卷网下载

一、选择题

1. 南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库。知该水库水位为海拔148.5m时，相应水面的面积为 $140.0 m^{2} ；$ 水位为海拔157.5m时，相应水面的面积为 $180.0 m^{2} .$ 将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m上升到157.5m时，增加的水量约为（） $(\sqrt{7} \approx 2.65)$

A、 $1.0 \times 10^{9} m^{3}$ B、 $1.2 \times 10^{9} m^{3}$ C、 $1.4 \times 10^{9} m^{3}$ D、 $1.6 \times 10^{9} m^{3}$

查看试题解析
2. 正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（）

A、 $20 + 12 \sqrt{3}$ B、 $28 \sqrt{2}$ C、 $\frac{56}{3}$ D、 $\frac{28 \sqrt{2}}{3}$

查看试题解析
3. 北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为 $36000 km$ （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O，半径r为 $6400 km$ 的球，其上点A的纬度是指 $O A$ 与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为 $α$ ，记卫星信号覆盖地球表面的表面积为 $S = 2 π r^{2} (1 - \cos α)$ （单位： ${km}^{2}$ ），则S占地球表面积的百分比约为（）

A、26% B、34% C、42% D、50%

查看试题解析
4. 已知圆锥的底面半径为 $\sqrt{2}$ ，其侧面展开图为一个半圆，则该圆锥的母线长为（）

A、2 B、2 $\sqrt{2}$ C、4 D、4 $\sqrt{2}$

查看试题解析
5. 若棱长为 $2 \sqrt{3}$ 的正方体的顶点都在同一球面上，则该球的表面积为（）

A、 $12 π$ B、 $24 π$ C、 $36 π$ D、 $144 π$

查看试题解析
6. 在三棱锥 $P - A B C$ 中， $△ A B C$ 是边长为2的等边三角形， $P A = P B = 2 ， P C = \sqrt{6}$ ，则该棱锥的体积为（）

A、1 B、 $\sqrt{3}$ C、2 D、3

查看试题解析
7. 在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $A B = 4 ， P C = P D = 3 ， ∠ P C A = 45 °$ ，则 $△ P B C$ 的面积为（）

A、 $2 \sqrt{2}$ B、 $3 \sqrt{2}$ C、 $4 \sqrt{2}$ D、 $5 \sqrt{2}$

查看试题解析
8. 在三棱锥 $P - A B C$ 中，线段 $P C$ 上的点 $M$ 满足 $P M = \frac{1}{3} P C$ ，线段 $P B$ 上的点 $N$ 满足 $P N = \frac{2}{3} P B$ ，则三棱锥 $P - A M N$ 和三棱锥 $P - A B C$ 的体积之比为（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
9. 已知圆锥PO的底面半径为 $\sqrt{3}$ ， O为底面圆心，PA，PB为圆锥的母线， $∠ A O B = 120 °$ ，若 $△ P A B$ 的面积等于 $\frac{9 \sqrt{3}}{4}$ ，则该圆锥的体积为（）

A、 $π$ B、 $\sqrt{6} π$ C、 $3 π$ D、 $3 \sqrt{6} π$

查看试题解析
10. 如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为 $120 °$ ，腰为3的等腰三角形，则该几何体的体积为（）

A、23 B、24 C、26 D、27

查看试题解析
11. 正三棱台高为1，上下底边长分别为 $3 \sqrt{3}$ 和 $4 \sqrt{3}$ ，所有顶点在同一球面上，则球的表面积是（）

A、100π B、128π C、144π D、192π

查看试题解析
12. 甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为 $2 π$ ，侧面积分别为 $S_{甲}$ 和 $S_{乙}$ ，体积分别为 $V_{甲}$ 和 $V_{乙}$ ．若 $\frac{S_{甲}}{S_{乙}} = 2$ ，则 $\frac{V_{甲}}{V_{乙}} =$ （）

A、 $\sqrt{5}$ B、 $2 \sqrt{2}$ C、 $\sqrt{10}$ D、 $\frac{5 \sqrt{10}}{4}$

查看试题解析
13. 已知球O的半径为1，四棱锥的顶点为O，底面的四个顶点均在球O的球面上，则当该四棱锥的体积最大时，其高为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
14. 已知正三棱锥 $P - A B C$ 的六条棱长均为6， $S$ 是 $△ A B C$ 及其内部的点构成的集合，设集合 $T = {Q \in S | P Q ⩽ 5}$ ，则 $T$ 表示的区域的面积为（）

A、 $\frac{3 π}{4}$ B、 $π$ C、 $2 π$ D、 $3 π$

查看试题解析
15. 定义：24小时内降水在平地上积水厚度（ $mm$ ）来判断降雨程度．其中小雨（ $< 10 mm$ ），中雨（ $10 mm - 25 mm$ ），大雨（ $25 mm - 50 mm$ ），暴雨（ $50 mm - 100 mm$ ），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）

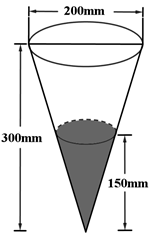A、小雨 B、中雨 C、大雨 D、暴雨

查看试题解析
16. 两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为 $\frac{32 π}{3}$ ，两个圆锥的高之比为 $1 ： 3$ ，则这两个圆锥的体积之和为（）

A、 $3 π$ B、 $4 π$ C、 $9 π$ D、 $12 π$

查看试题解析
17. 已知△ABC是面积为 $\frac{9 \sqrt{3}}{4}$ 的等边三角形，且其顶点都在球O的球面上.若球O的表面积为16π，则O到平面ABC的距离为（）

A、 $\sqrt{3}$ B、 $\frac{3}{2}$ C、1 D、 $\frac{\sqrt{3}}{2}$

查看试题解析
18. 埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（）

A、 $\frac{\sqrt{5} - 1}{4}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{5} + 1}{4}$ D、 $\frac{\sqrt{5} + 1}{2}$

查看试题解析
19. 已知 $A ， B ， C$ 为球O的球面上的三个点，⊙ $O_{1}$ 为 $△ A B C$ 的外接圆，若⊙ $O_{1}$ 的面积为 $4 π$ ， $A B = B C = A C = O O_{1}$ ，则球O的表面积为（）

A、 $64 π$ B、 $48 π$ C、 $36 π$ D、 $32 π$

查看试题解析
20. 已知圆柱的上、下底面的中心分别为O₁ ， O₂ ，过直线O₁O₂的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）

A、 $12 \sqrt{2} π$ B、12π C、 $8 \sqrt{2} π$ D、 $10 π$

查看试题解析
21. 已知A,B,C是半径为1的求O的球面上的三个点，且AC⊥BC,AC=BC=1，则三棱锥O-ABC的体积为（）

A、 $\frac{\sqrt{2}}{12}$ B、 $\frac{\sqrt{3}}{12}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
22. 已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，∆ABC是边长为2的正三角形，E、F，分别是PA，AB的中点， $∠$ CEF=90°，则球O的体积为（）

A、 $8 \sqrt{6} π$ B、 $4 \sqrt{6} π$ C、 $2 \sqrt{6} π$ D、 $\sqrt{6} π$

查看试题解析
23. 已知四面体ABCD中，棱BC，AD所在直线所成的角为60°，且BC=2，AD=3，∠ACD=120°，则四面体ABCD体积的最大值是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{9}{4}$ D、 $\frac{3}{4}$

查看试题解析

二、多项选择题

24. 已知圆锥的顶点为 $P$ ，底面圆心为 $O$ ， $A ， B$ 为底面直径， $∠ A P B = 120 °$ ， $P A = 2$ ，点 $C$ 在底面圆周上，且二面角 $P - A C - O$ 为45°，则（）

A、该圆锥的体积为 $π$ B、该圆锥的侧面积为 $4 \sqrt{3} π$ C、 $A C = 2 \sqrt{2}$ D、 $△ P A C$ 的面积为 $\sqrt{3}$

查看试题解析
25. 如图，四边形 $A B C D$ 为正方形， $E D ⊥$ 平面 $A B C D$ ， $F B ∥ E D ， A B = E D = 2 F B$ ，记三棱锥 $E - A C D$ ， $F - A B C$ ， $F - A C E$ 的体积分别为 $V_{1} ， V_{2} ， V_{3}$ ，则（）

A、 $V_{3} = 2 V_{2}$ B、 $V_{3} = 2 V_{1}$ C、 $V_{3} = V_{1} + V_{2}$ D、 $2 V_{3} = 3 V_{1}$

查看试题解析
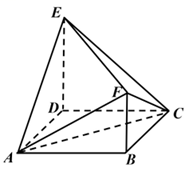26. 在正三棱柱ABC- $A_{1} B_{1} C_{1}$ 中，AB=AA₁=1，点P满足 $\vec{B P} = λ \vec{B C} + μ \vec{B B_{1}}$ ，其中λ∈[0，1]， $μ$ ∈[0，1]，则（）

A、当λ=1时，△ $A B_{1}$ P的周长为定值 B、当 $μ$ =1时，三棱锥P-A₁BC的体积为定值 C、当λ= $\frac{1}{2}$ 时，有且仅有一个点P，使得 $A_{1} P ⊥ B P$ D、当 $μ$ = $\frac{1}{2}$ 时，有且仅有一个点P，使得 $A_{1}$ B⊥平面A $B_{1}$ P

查看试题解析

三、填空题

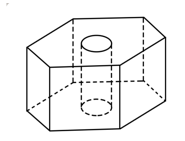
27. 底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为 .

查看试题解析
28. 已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为．

查看试题解析
29. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F分别为CD， $A_{1} B_{1}$ 的中点，则以EF为直径的球面与正方体每条棱的交点总数为．

查看试题解析
30. 已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为．

查看试题解析
31. 已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为．

查看试题解析
32. 已知直四棱柱ABCD–A₁B₁C₁D₁的棱长均为2，∠BAD=60°．以 $D_{1}$ 为球心， $\sqrt{5}$ 为半径的球面与侧面BCC₁B₁的交线长为．

查看试题解析
33. 如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm，高为2 cm，内孔半轻为0.5 cm，则此六角螺帽毛坯的体积是cm.

查看试题解析
34. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是120，E为 $C C_{1}$ 的中点，则三棱锥E-BCD的体积是.

查看试题解析
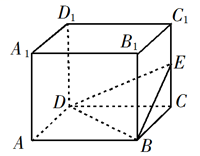35. 已知四棱锥的底面是边长为 $\sqrt{2}$ 的正方形，侧棱长均为 $\sqrt{5}$ .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为.

查看试题解析
36. 学生到工厂劳动实践，利用3D打印技术制作模型，如图，该模型为长方体ABCD-A₁B₁C₁D₁ ，挖去四棱推O一EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H，分别为所在棱的中点，AB=BC=6cm，AA₁=4cm，3D打印所用原料密度为0.9g/cm² ，不考虑打印损耗，制作该模型所需原料的质量为g.

查看试题解析
37. 已知点 $S ， A ， B ， C$ 均在半径为2的球面上， $△ A B C$ 是边长为3的等边三角形， $S A ⊥$ 平面 $A B C$ ，则 $S A =$ ．

查看试题解析