2023年浙教版数学七年级上册第四章代数式单元测试（B卷）

试卷更新日期：2023-09-02 类型：单元试卷

进入出卷网下载

一、选择题（每题2分，共20分）

1. 下列说法正确的是（）

A、多项式 $x^{2} - 2 x - 1$ 的常数项是1 B、多项式 $x^{2} y - 2 y - 1$ 是二次三项式 C、 $\frac{x + y}{2}$ 是单项式 D、多项式 $- x^{2} y + 2 y$ 最高次项的系数是－1

查看试题解析
2. “居家嗨购，网上过年”，为做好疫情防控并促进春节消费，山西省组织开展了2022年“全晋乐购”网上年货节活动，某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工，该企业选购了甲种物品 $(a + 3)$ 件，单价是100元；乙种物品 $a$ 件，单价是240元．则该企业共花费在（）

A、 $(140 a + 300)$ 元 B、 $(200 a + 300)$ 元 C、 $(300 a + 300)$ 元 D、 $(340 a + 300)$ 元

查看试题解析
3. 已知 $4 a - 3 b^{3} = 7$ ， $3 a + 2 b^{3} = 9$ ，则 $a - 5 b^{3}$ 的值为（）

A、 $- 2$ B、2 C、14 D、16

查看试题解析
4. 如图，直线上的四个点 $A$ ， $B$ ， $C$ ， $D$ 分别代表四个小区，其中 $A$ 小区和 $B$ 小区相距 $a m$ ， $B$ 小区和 $C$ 小区相距 $200 m$ ， $C$ 小区和 $D$ 小区相距 $a m$ ，某公司的员工在 $A$ 小区有30人， $B$ 小区有5人. $C$ 小区有20人， $D$ 小区有6人，现公司计划在 $A$ ， $B$ ， $C$ ， $D$ 四个小区中选一个作为班车停靠点，为使所有员工步行到停靠点的路程总和最小，那么停靠点的位置应设在（）

A、 $A$ 小区 B、 $B$ 小区 C、 $C$ 小区 D、 $D$ 小区

查看试题解析
5. 已知数轴上的四点 $P$ ， $Q$ ， $R$ ， $S$ 对应的数分别为 $p$ ， $q$ ， $r$ ， $s$ ．且 $p$ ， $q$ ， $r$ ， $s$ 在数轴上的位置如图所示，若 $r - p = 10$ ， $s - p = 12$ ， $s - q = 9$ ，则 $r - q$ 等于（）．

A、7 B、9 C、11 D、13

查看试题解析
6. 在计算：M-(5x²-3x-6)时，嘉琪同学将括号前面的“-”号抄成了“+”号，得到的运算结果是-2x²+3x-4，你认为多项式M是（）

A、-7x²+6x+2 B、-7x²-6x-2 C、-7x²+6x-2 D、-7x²-6x+2

查看试题解析
7. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，且 $| c | > | a | > | b |$ ，则 $| a + b | - 2 | c - b | + | a + c | =$ （）．

A、 $c - b$ B、0 C、 $3 b - 3 c$ D、 $2 a + 3 b - c$

查看试题解析
8. 多项式 $36 x^{2} - 3 x + 5$ 与 $3 x^{3} + 12 m x^{2} - 5 x + 7$ 相加后，不含二次项，则常数 $m$ 的值是（）

A、2 B、-8 C、-2 D、-3

查看试题解析
9. 图1是由3个相同小长方形拼成的图形其周长为24 $c m$ ，图2中的长方形 $A B C D$ 内放置10个相同的小长方形，则长方形 $A B C D$ 的周长为（）

A、 $32 c m$ B、 $36 c m$ C、 $48 c m$ D、 $60 c m$

查看试题解析
10. 现有1张大长方形和3张相同的小长方形卡片，按如图所示两种方式摆放，则小长方形的长与宽的差是（）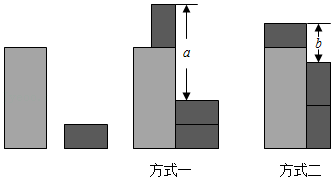

A、a-b B、 $\frac{a - b}{2}$ C、 $\frac{a - b}{3}$ D、 $\frac{a + b}{3}$

查看试题解析

二、填空题（每空3分，共21分）

11. 有一个长方体水箱，从里面量得它的深度为 $30 c m$ ，底面长为 $25 c m$ ，宽为 $20 c m$ ，水箱里已盛有深度为 $a (c m) (a \leq 30)$ 的水.若往水箱里放入一个棱长为 $10 c m$ 的立方体铁块，则水箱的水深为 $c m$ .

查看试题解析
12. 若（x-1）⁴（x+2）⁵=a₀+a₁x+a₂x²+…+ a₉x⁹ ，求：a₁+a₃+a₅+a₇+a₉= ．

查看试题解析
13. 若代数式2ax²y+3xy﹣4﹣5x²y﹣7x﹣7ax²y+m中，化简后不含x²y项，则a²⁰¹⁹﹣4＝．

查看试题解析
14. 已知 $- 5 a^{2 m} b$ 和 $3 a^{4} b^{3 - n}$ 是同类项，则 $\frac{1}{2}$ m-n的值是．

查看试题解析
15. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“英华数”，定义新运算：将一个“英华数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω （ 27 ）$ ．

(2)、若m，n都是“英华数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析
16. 已知A，B，C三个车站的位置如图所示，则B，C间的距离等于.

查看试题解析

三、解答题（共11题，共79分）

17. 已知有理数a和b满足多项式A，且A=（a﹣1）x⁵+x^|b+2|﹣2x²+bx+b（b≠﹣2）是关于x的二次三项式，求（a﹣b）²的值．

查看试题解析
18. 如果多项式 $x^{4} - (a - 1) x^{3} + 5 x^{2} - (b + 1) x - 1$ 中不含 $x$ 的三次项和 $x$ 的一次项，求 $| - 7 a - b^{3} |$ 的值.

查看试题解析
19. 已知 A=3x²+3y²-2xy，B=xy-2y²-2x².
求：

(1)、2A-3B.

(2)、若|2x-3|=1，y²=9，|x-y|=y-x，求 2A-3B 的值.

(3)、若 x=2，y=-4 时，代数式 ax³+ $\frac{1}{2}$ by+5=17，那么当 x=-4，y=- $\frac{1}{2}$ 时，求代数式3ax-24by³+6 的值.

查看试题解析
20.

(1)、阅读材料：我们知道， $4 x + 2 x - x = (4 + 2 - 1) x = 5 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) + 2 (a + b) - (a + b) - (4 + 2 - 1) (a + b) = 5 (a + b)$ ． “整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．
尝试应用：
①把 $(a + b)$ 看成一个整体，合并 $- 3 (a + b)^{2} - 6 (a + b)^{2} + 8 (a + b)^{2}$ 的结果 ▲ ．
②拓广探索：已知 $a - 2 b = 5 ， 2 b - c = - 7 ， c - d = 12$ ，求 $4 (a - c) + 4 (2 b - d) - 4 (2 b - c)$ 的值．

(2)、某人用400元购买了8套电子产品，准备以一定价格出售，如果每套电子产品以56元的价格作为标准卖出，超出的记为正数，不足的记为负数，记录如下（单位：元）：
$- 3 ， + 7 ， - 8 ， + 9 ， - 2 ， 0 ， - 1 ， - 6$ ．
当他卖完这8套电子产品后是盈利还是亏损？

查看试题解析
21. 有这样一道题“如果代数式 $5 a + 3 b$ 的值为 $- 4$ ，那么代数式 $2 (a + b) + 4 (2 a + b)$ 的值是多少？”爱动脑筋的吴爱国同学这样来解：原式 $= 2 a + 2 b + 8 a + 4 b = 10 a + 6 b$ ．我们把 $5 a + 3 b$ 看成一个整体，把式子 $5 a + 3 b = - 4$ 两边乘以2得 $10 a + 6 b = - 8$ ．整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照上面的解题方法，完成下面问题：

(1)、【简单应用】
已知 $a^{2} - 2 a = 1$ ，则 $2 a^{2} - 4 a + 1$ = ．

(2)、已知 $m + n = 2$ ， $m n = - 4$ ，求 $2 (m n - 3 m) - 3 (2 n - m n)$ 的值．

(3)、【拓展提高】
已知 $a^{2} + 2 a b = - 5$ ， $a b - 2 b^{2} = - 3$ ，求代数式 $3 a^{2} + 4 a b + 4 b^{2}$ 的值．

查看试题解析
22. 已知整式P＝x²+x﹣1，Q＝x²﹣x+1，R＝﹣x²+x+1，若一个次数不高于二次的整式可以表示为aP+bQ+cR（其中a，b，c为常数）.则可以进行如下分类
①若a≠0，b＝c＝0，则称该整式为P类整式；

②若a≠0，b≠0，c＝0，则称该整式为PQ类整式；

③若a≠0，b≠0，c≠0.则称该整式为PQR类整式；

(1)、模仿上面的分类方式，请给出R类整式和QR类整式的定义，若，则称该整式为“R类整式”，若，则称该整式为“QR类整式”；

(2)、说明整式x²﹣5x+5为“PQ类整式；

(3)、x²+x+1是哪一类整式？说明理由.

查看试题解析
23. 已知：b是最小的正整数，且a、b、c满足（c﹣5）²+|a+b|＝0，请回答问题：

(1)、请直接写出a、b、c的值．a＝，b＝，c＝

(2)、a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x，点P在0到2之间运动时（即0≤x≤2时），请化简式子：|x+1|﹣|x﹣1|+2|x+5|（请写出化简过程）

(3)、在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC﹣AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值

查看试题解析
24. 发现：一个三位数的百位上数字为a，十位上数字为(a+1)，个位上数字为(a＋2)；把这个三位数的百位上数字与个位上的数字交换得到一个新三位数，新三位数与原三位数的差是9的倍数．

(1)、验证：
①765—567=9× ▲ ；
②通过列式计算，说明新三位数与原三位数的差是9的倍数；

(2)、延伸：新三位数与原三位数的和是正整数m的倍数，则m= ▲ ，并说明理由．

查看试题解析
25. 如图长为 $60 cm$ ，宽为 $x (cm)$ 的大长方形被分割为了7小块，除阴影 $A ， B$ 外，其余5块是形状大小完全相同的小长方形，其中小长方形的较短一边长度为 $10 cm$ ．

(1)、从图可知每块小长方形的较长的一边长度是．代数式 $x - 30 ， x - 40$ 中，哪一个代数式的值为正数？．

(2)、请你先用含x的代数式表示阴影 $A ， B$ 的面积，并说明阴影A的面积一定比阴影B的面积大 ${300cm}^{2}$ ．

(3)、设阴影A和B的面积之和为 $S ({cm}^{2})$ ，阴影A和B的周长之和为 $C (cm)$ ，则代数式“ $S - C$ ”的结果是正数还是负数还是有可能为零？请你先作出判断，再说明理由．

查看试题解析

26. 某果农计划从甲、乙两个仓库用汽车向A，B两个果园运送有机化肥，甲、乙两个仓库分别可运出80吨和100吨有机化肥；A，B两个果园分别需用110吨和70吨有机化肥.从甲、乙两个仓库到A，B两个果园的运价如下表所示：

	甲仓库	乙仓库
到A果园	每吨15元	每吨25元
到B果园	每吨20元	每吨20元

设从甲仓库运往A果园x吨有机化肥.

(1)、从甲仓库运往B果园吨有机化肥；从乙仓库运往A果园吨有机化肥，运往B果园吨有机化肥（用含x的式子表示，填最简结果）；

(2)、求从这两个仓库往两个果园运送有机化肥的总运费（用含x的式子表示）；

(3)、当

x = 80

时，求从这两个仓库往两个果园运送有机化肥的总运费.

查看试题解析

27. 2022年“双十一”期间，很多国货品牌受到人们的青睐，销量大幅增长．某平台的体育用品旗舰店实行优惠销售，规定如下：对原价 $160$ 元/件的某款运动速干衣和 $20$ 元/双的某款运动棉袜开展促销活动，活动期间向客户提供两种优惠方案．
方案A：买一件运动速干衣送一双运动棉袜；

方案B：运动速干衣和运动棉袜均按9折付款．

某户外俱乐部准备购买运动速干衣 $30$ 件，运动棉袜x双 $(x \geq 30)$ ．

(1)、若该户外俱乐部按方案A购买，需付款元（用含x的式子表示）；若该户外俱乐部按方案B购买，需付款元（用含x的式子表示）；

(2)、若 $x = 40$ ，通过计算说明此时按哪种方案购买较为合算；

(3)、若 $x = 40$ ，你能设计最省钱的购买方案吗？写出你的购买方法，并计算需要付款多少元？

查看试题解析

2023年浙教版数学七年级上册第四章 代数式 单元测试（B卷）

一、选择题（每题2分，共20分）

二、填空题（每空3分，共21分）

三、解答题（共11题，共79分）

2023年浙教版数学七年级上册第四章代数式单元测试（B卷）